功能介绍

登录系统：管理员需要输入正确的用户名和密码来登录系统，从而完成各类信息的管理工作；

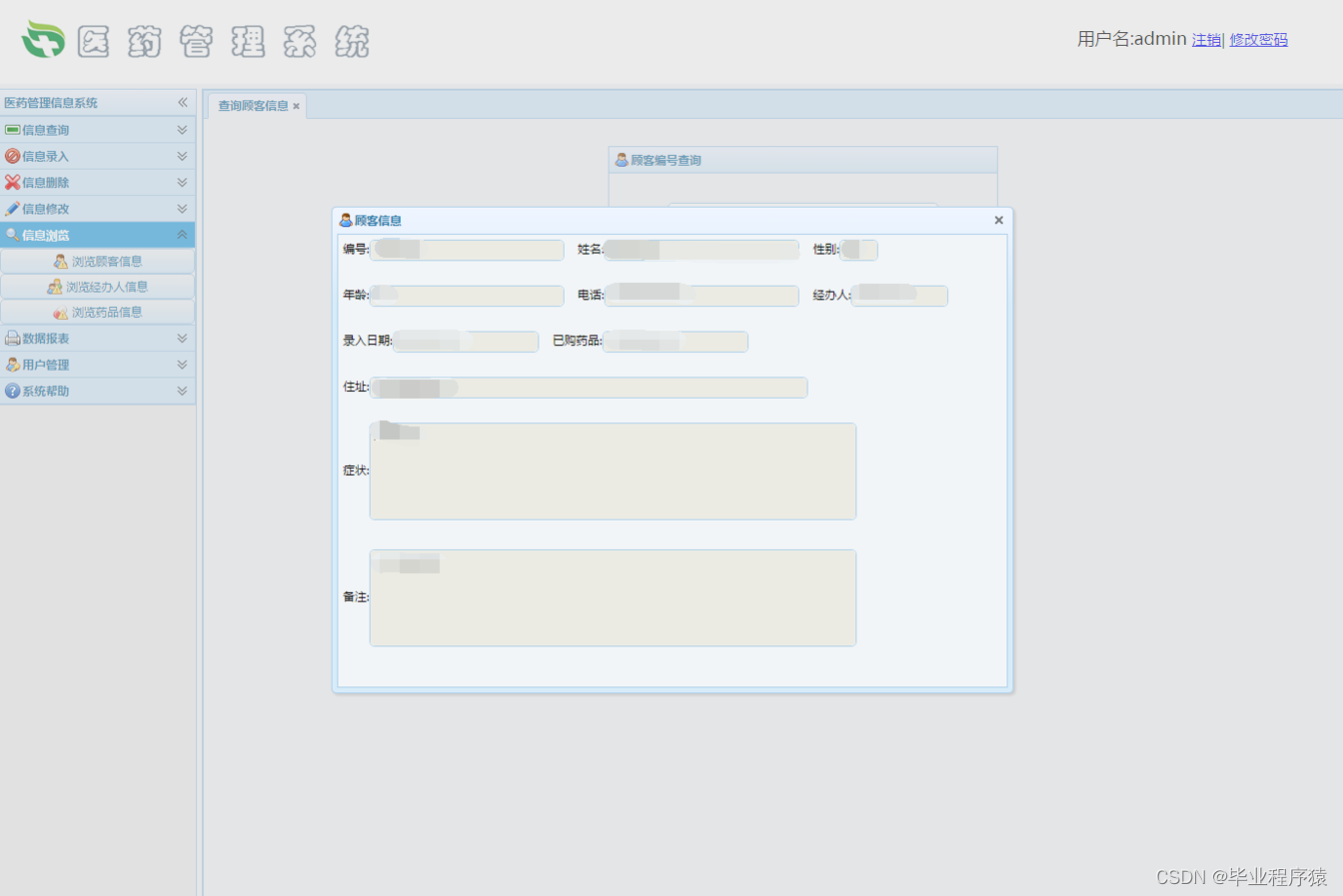
信息查询：查询客户信息、查询经办人信息、查询药品信息；

信息录入：录入顾客信息、录入经办人信息、录入药品信息；

信息修改：删除顾客信息、删除经办人信息、删除药品信息；

信息浏览：浏览顾客信息、删除经办人信息、删除药品信息；

数据报表：顾客信息报表、经办人信息报表、药品信息报表；

用户管理：管理系统的各个管理员信息。

部分功能模块代码

package mms.controller;import org.springframework.beans.factory.annotation.Autowired;import org.springframework.stereotype.Controller;
import org.springframework.web.bind.annotation.RequestMapping;
import org.springframework.web.bind.annotation.RequestParam;
import org.springframework.web.bind.annotation.ResponseBody;import mms.pojo.Agency;
import mms.pojo.EasyUIResult;
import mms.services.AgencyService;@RequestMapping("Agency")
@Controller
public class AgencyController {// 经办人controller@Autowiredprivate AgencyService agencyService;// 通过ano查询单个经办人@RequestMapping("GetAgency")@ResponseBodypublic Agency queryAgencyByAno(String ano) {Agency agency = agencyService.queryAgencyByAno(ano);return agency;}@RequestMapping(value = "DeleteAgency", produces = "text/html;charset=UTF-8")@ResponseBody// 按编号删除public String deleteAgencyByAno(String ano) {return agencyService.deleteAgencyByAno(ano);}// 批量删除@RequestMapping(value = "DeleteRows", produces = "text/html;charset=UTF-8")@ResponseBodypublic String deleteAgencyByRows(@RequestParam(value = "array[]") String[] array) {try {return agencyService.deleteAgencyByRows(array);} catch (Exception e) {// TODO: handle exception// 捕获异常，spring进行事务回滚return "操作异常，，某些经办人处理过顾客信息,无法删除该经办人，请重新选择";}}// 修改经办人信息@RequestMapping(value = "ModifyAgency", produces = "text/html;charset=UTF-8")@ResponseBodypublic String modifyAgency(Agency agency) {return agencyService.modifyAgency(agency);}// easyui数据表格返回全部经办人json@RequestMapping("GetMessage")@ResponseBodypublic EasyUIResult queryAllAgency(@RequestParam(value = "page", defaultValue = "1") Integer page,@RequestParam(value = "rows", defaultValue = "5") Integer rows) {return this.agencyService.queryAllAgency(page, rows);}// 保存经办人信息@RequestMapping(value = "SaveAgency", produces = "text/html;charset=UTF-8")@ResponseBodypublic String saveAgency(Agency agency) {return agencyService.saveAgency(agency);}// 返回所有经办人@RequestMapping("GetAllAgency")@ResponseBodypublic java.util.List<Agency> getAllAgency() {java.util.List<Agency> allAgency = agencyService.getAllAgency();return allAgency;}
}
package mms.services;import java.util.List;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.stereotype.Service;
import org.springframework.transaction.annotation.Transactional;
import org.springframework.transaction.interceptor.TransactionAspectSupport;import com.github.pagehelper.PageHelper;
import com.github.pagehelper.PageInfo;
import mms.mapper.AgencyMapper;
import mms.pojo.Agency;
import mms.pojo.EasyUIResult;/*经办人service
处理业务逻辑*/
@Service
@Transactional
public class AgencyService {// 注入mapper@Autowiredprivate AgencyMapper agencyMapper;public Agency queryAgencyByAno(String ano) {// TODO Auto-generated method stubAgency agency = agencyMapper.queryAgencyByAno(ano);return agency;}public EasyUIResult queryAllAgency(Integer page, Integer rows) {// TODO Auto-generated method stubPageHelper.startPage(page, rows);List<Agency> agencies = agencyMapper.queryAllAgency();PageInfo<Agency> pageInfo = new PageInfo<Agency>(agencies);return new EasyUIResult(pageInfo.getTotal(), agencies);}public String saveAgency(Agency agency) {// TODO Auto-generated method stubtry {if (queryAgencyByAno(agency.getAno()) != null) {return "经办人编号已经存在，请重新输入编号";}agencyMapper.saveAgency(agency);return "保存成功";} catch (Exception e) {// TODO: handle exceptionreturn "操作异常，请刷新后操作";}}public String deleteAgencyByAno(String ano) {// TODO Auto-generated method stubtry {agencyMapper.deleteAgencyByAno(ano);} catch (Exception e) {// TODO: handle exceptionreturn "删除失败，此经办人为客户提供过服务，" + "无法删除此经办人";}return "删除成功";}public String modifyAgency(Agency agency) {// TODO Auto-generated method stubAgency queryAgencyByAno = queryAgencyByAno(agency.getAno());if (queryAgencyByAno != null) {if (queryAgencyByAno.getAid() != agency.getAid())return "这个经办人编号已经存在，不能修改为这个编号";}try {agencyMapper.modifyAgency(agency);} catch (Exception e) {// TODO: handle exceptionreturn "修改失败，可能是有客户在此经办人购药，" + "无法修改编号";}// agencyMapper.modifyAgency(agency);return "修改成功";}public List<Agency> getAllAgency() {// TODO Auto-generated method stubList<Agency> allAgency = agencyMapper.queryAllAgency();return allAgency;}public String deleteAgencyByRows(String[] array) {// TODO Auto-generated method stubtry {for (String ano : array) {agencyMapper.deleteAgencyByAno(ano);}} catch (Exception e) {// TODO: handle exception// 抛出异常让spring捕获，进行事务回滚throw new RuntimeException();}return "删除成功";}}
package mms.mapper;import java.util.List;
import mms.pojo.Agency;public interface AgencyMapper {public Agency queryAgencyByAno(String ano);public void saveAgency(Agency agency);public List<Agency> queryAllAgency();public void deleteAgencyByAno(String ano);public void modifyAgency(Agency agency);
}