文章目录
- 一、简介
- 二 、一元高斯分布
- 三、多元高斯分布
- 1、独立多元高斯分布
- 2、多元相关变量高斯分布
一、简介
高斯分布是一种重要的模型,也被称作正态分布,其广泛应用与连续型随机变量的分布中。在数据分析领域中高斯分布占有重要地位。掌握高斯分布是学习数据分析的重要基础,下面就结合理论公式和其几何图形来阐述。
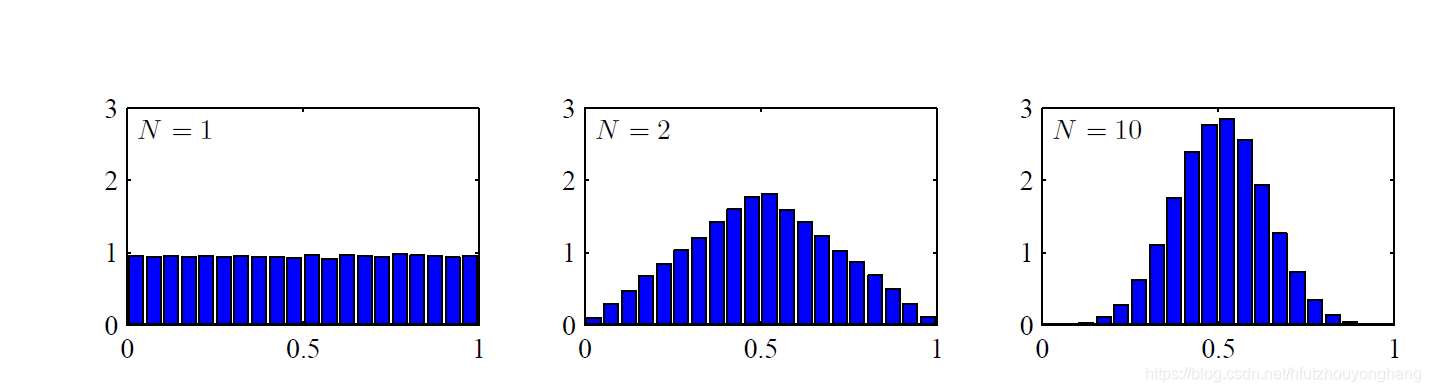
高斯分布会在许多问题中产生。例如,对于一个一元实值向量,使熵取得最大值的是高斯分布;中心极限定理告诉我们:一组随机变量之和的概率分布随着和式中项的数量的增加而逐渐趋向于高斯分布。如果有N个均匀分布在区间 [ 0 , 1 ] [0,1] [0,1]的变量 x 1 , x 2 , . . . , x N x_1,x_2,...,x_N x1,x2,...,xN,其均值 1 N ∑ i = 1 i = N x i \frac{1}{N}\sum_{i=1}^{i=N}x_i N1∑i=1i=Nxi的分布,对于N很大时,这个分布趋向于高斯分布,当N增大时,其均值的分布如下图(图片来源于:《模式识别与机器学习》)所示。
二 、一元高斯分布
若随机变量 X X X服从均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2的高斯分布,那么:
f ( x ; μ , σ ) = 1 σ ( 2 π ) 1 2 e x p ( − ( x − μ ) 2 2 σ 2 ) f(x;\mu,\sigma)= \dfrac{1}{\sigma(2\pi)^{\frac{1}{2}}}exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) f(x;μ,σ)=σ(2π)211exp(−2σ2(x−μ)2)
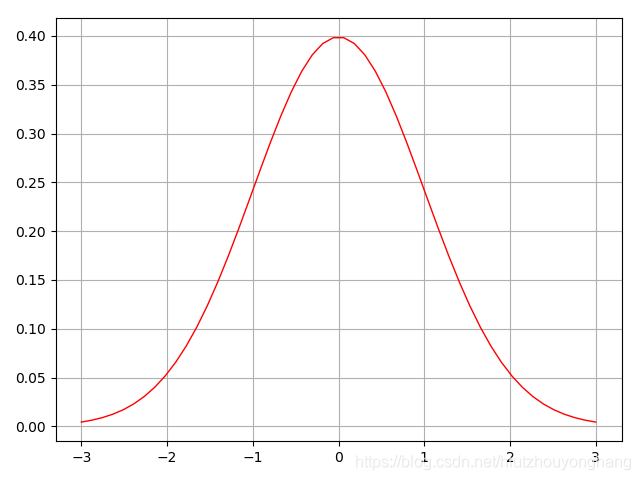
高斯分布的图形像钟一样,下图展示了一般正态分布的图形。其中 μ = 0 , σ = 1 \mu=0,\sigma=1 μ=0,σ=1。
对于一个非标准的正态分布,可以由标准正态分布经过以下3步变换得到:
- 将x向右移动u个单位
- 将密度函数x轴延展sigma倍
- 将函数密度图像y轴压缩 σ \sigma σ倍
如果 X X X服从分布, X ∼ N ( μ , σ 2 ) X\thicksim N(\mu,\sigma^2) X∼N(μ,σ2),那么具有以下的性质:
- 如果 a , b a,b a,b是实数,那么 a X + b ∼ N ( a μ + b , ( a σ ) 2 ) aX+b\thicksim N(a\mu+b,(a\sigma)^2) aX+b∼N(aμ+b,(aσ)2)
- 如果 Y ∼ N ( μ y , σ y 2 ) Y\thicksim N(\mu_y,\sigma_y^2) Y∼N(μy,σy2), X ∼ N ( μ x , σ x 2 ) X\thicksim N(\mu_x,\sigma_x^2) X∼N(μx,σx2),且 X , Y X,Y X,Y相互独立,那么 X + Y ∼ N ( μ x + μ y , σ x 2 + σ y 2 ) X+Y\thicksim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2) X+Y∼N(μx+μy,σx2+σy2), X − Y ∼ N ( μ x − μ y , σ x 2 + σ y 2 ) X-Y\thicksim N(\mu_x-\mu_y,\sigma_x^2+\sigma_y^2) X−Y∼N(μx−μy,σx2+σy2)
- 如果 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn为独立标准正态分布,那么 X 1 2 + X 2 2 + . . . + X n 2 X_1^2+X_2^2+...+X_n^2 X12+X22+...+Xn2服从自由度为n的卡方分布。
三、多元高斯分布
1、独立多元高斯分布
假设 n n n个变量 x = [ x 1 , x 2 , . . . , x n ] T \boldsymbol{x}=[x_1,x_2,...,x_n]^T x=[x1,x2,...,xn]T相互独立,且服从高斯分布,各个维度的均值 E ( x ) = [ u 1 , u 2 , . . . , u n ] T E(\boldsymbol{x})=[u_1,u_2,...,u_n]^T E(x)=[u1,u2,...,un]T ,方差 σ ( x ) = [ σ 1 , σ 2 , . . . , σ n ] T \sigma(\boldsymbol{x})=[\sigma_1,\sigma_2,...,\sigma_n]^T σ(x)=[σ1,σ2,...,σn]T,根据联合概率密度公式有:
f ( x ) = p ( x 1 , x 2 , . . . , x n ) = p ( x 1 ) p ( x 2 ) . . . p ( x n ) = 1 ( 2 π ) n σ 1 σ 2 . . . σ n e − ( x 1 − u 1 ) 2 2 σ 1 2 − ( x 2 − u 2 ) 2 2 σ 2 2 . . . − ( x n − u n ) 2 2 σ n 2 f(\boldsymbol{x})=p(x_1,x_2,...,x_n)=p(x_1)p(x_2)...p(x_n)=\dfrac{1}{(\sqrt{2\pi})^n\sigma_1\sigma_2...\sigma_n} e^{-\frac{(x_1-u_1)^2}{2\sigma_1^2}-\frac{(x_2-u_2)^2}{2\sigma_2^2}...-\frac{(x_n-u_n)^2}{2\sigma_n^2}} f(x)=p(x1,x2,...,xn)=p(x1)p(x2)...p(xn)=(2π)nσ1σ2...σn1e−2σ12(x1−u1)2−2σ22(x2−u2)2...−2σn2(xn−un)2
如果我们令:
z 2 = ( x 1 − u 1 ) 2 2 σ 1 2 + ( x 2 − u 2 ) 2 2 σ 2 2 . . . + ( x n − u n ) 2 2 σ n 2 , σ z = σ 1 σ 2 . . . σ n z^2=\frac{(x_1-u_1)^2}{2\sigma_1^2}+\frac{(x_2-u_2)^2}{2\sigma_2^2}...+\frac{(x_n-u_n)^2}{2\sigma_n^2} , \space\space\space\space\space\space\space\sigma_z=\sigma_1\sigma_2...\sigma_n z2=2σ12(x1−u1)2+2σ22(x2−u2)2...+2σn2(xn−un)2, σz=σ1σ2...σn
我们有:
f ( z ) = 1 ( 2 π ) n 2 σ z e − z 2 f(z)= \dfrac{1}{(2\pi)^{\frac{n}{2}}\sigma_z}e^{-z^2} f(z)=(2π)2nσz1e−z2
使用矩阵的形式来表示的话,则有:
z 2 = [ x 1 − u 1 , x 2 − u 2 , . . . , x n − u n ] [ σ 1 − 2 0 0 . . . 0 0 σ 2 − 2 0 . . . 0 . . . . . . . . . . . . . . . . . . . . . 0 0 0 . . . σ n − 2 ] [ x 1 − u 1 , x 2 − u 2 , . . . , x n − u n ] T z^2=[x_1-u_1,x_2-u_2,...,x_n-u_n] \begin{bmatrix}\sigma_1^{-2} & 0 &0 &...& 0 \\ 0 & \sigma_2^{-2} & 0 & ...&0 \\ .&.&.&...&.\\.&.&.&...&.\\.&.&.&...&.\\0&0&0&...&\sigma_n^{-2} \end{bmatrix} [x_1-u_1,x_2-u_2,...,x_n-u_n]^T z2=[x1−u1,x2−u2,...,xn−un]⎣⎢⎢⎢⎢⎢⎢⎡σ1−20...00σ2−2...000...0..................00...σn−2⎦⎥⎥⎥⎥⎥⎥⎤[x1−u1,x2−u2,...,xn−un]T
定义符号:
x − u x = [ x 1 − u 1 , x 2 − u 2 , . . . , x n − u n ] T \boldsymbol{x-u_x} = [x_1-u_1,x_2-u_2,...,x_n-u_n]^T x−ux=[x1−u1,x2−u2,...,xn−un]T
Σ = [ σ 1 2 0 0 . . . 0 0 σ 2 2 0 . . . 0 . . . . . . . . . . . . . . . . . . . . . 0 0 0 . . . σ n 2 ] \boldsymbol\Sigma= \begin{bmatrix}\sigma_1^{2} & 0 &0 &...& 0 \\ 0 & \sigma_2^{2} & 0 & ...&0 \\ .&.&.&...&.\\.&.&.&...&.\\.&.&.&...&.\\0&0&0&...&\sigma_n^{2} \end{bmatrix} Σ=⎣⎢⎢⎢⎢⎢⎢⎡σ120...00σ22...000...0..................00...σn2⎦⎥⎥⎥⎥⎥⎥⎤
σ z = ∣ Σ ∣ 1 2 \sigma_z=| \boldsymbol\Sigma|^{\frac{1}{2}} σz=∣Σ∣21
变量代换可得:
f ( z ) = 1 ( 2 π ) n 2 σ z e − z 2 = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e ( x − u x ) T ( Σ ) − 1 ( x − u x ) f(z)= \dfrac{1}{(2\pi)^{\frac{n}{2}}\sigma_z}e^{-z^2}= \dfrac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}e^{\boldsymbol{(x-u_x)^T} (\boldsymbol\Sigma)^{-1} \boldsymbol{(x-u_x)}} f(z)=(2π)2nσz1e−z2=(2π)2n∣Σ∣211e(x−ux)T(Σ)−1(x−ux)
下面以 x = [ x 1 , x 2 ] \boldsymbol x=[x_1,x_2] x=[x1,x2] 为例,画出二元高斯分布在变量之间相互独立的图像:
-
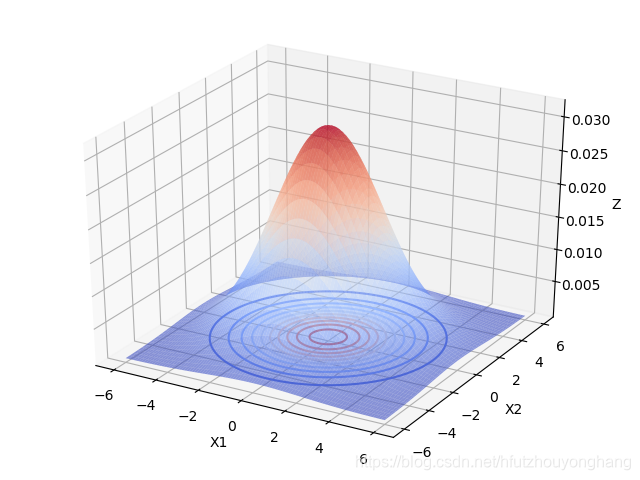
当 u = [ 0 , 0 ] Σ = [ 5 0 0 5 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}5&0 \\ 0 &5\end{bmatrix} u=[0,0]Σ=[5005]时:
-
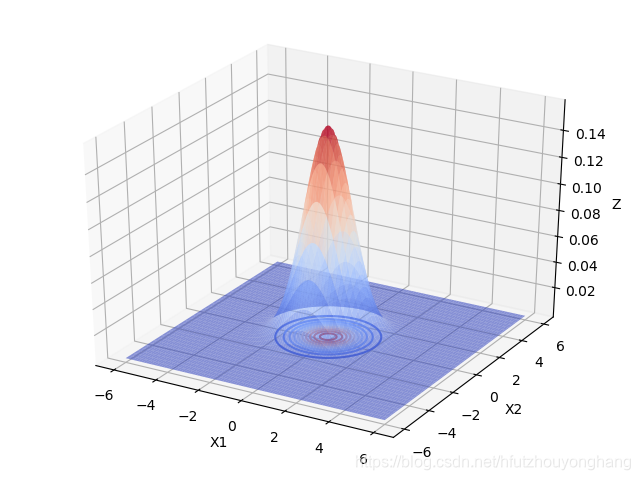
当 u = [ 0 , 0 ] Σ = [ 1 0 0 1 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}1&0 \\ 0 &1\end{bmatrix} u=[0,0]Σ=[1001]时:
-
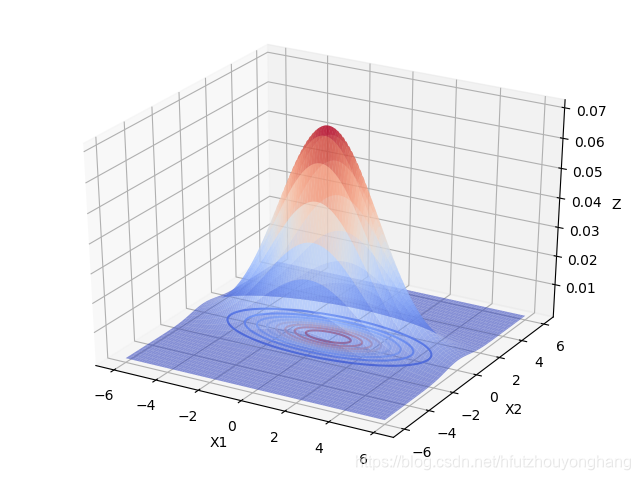
当 u = [ 0 , 0 ] Σ = [ 5 0 0 1 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}5&0 \\ 0 &1\end{bmatrix} u=[0,0]Σ=[5001]时:
-
- 当 u = [ 0 , 0 ] Σ = [ 1 0 0 5 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}1&0 \\ 0 &5\end{bmatrix} u=[0,0]Σ=[1005]时:
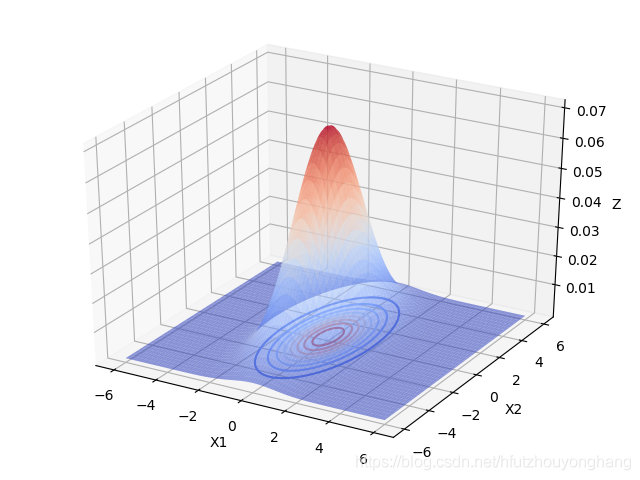
- 当 u = [ 0 , 0 ] Σ = [ 1 0 0 5 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}1&0 \\ 0 &5\end{bmatrix} u=[0,0]Σ=[1005]时:
由上图可以看出,当变量之间相互独立的时候:
- 当协方差矩阵的特征值越小时,分布函数图像越高越尖。
- 当协方差矩阵的特征值相等时,分布函数图像在X1,X2面上的投影是圆形的。当特征值不相等时,分布函数图像在X1,X2面上的投影是椭圆形的,X1,X2相互独立时,椭圆的长轴和短轴平行与坐标轴。且变量对应的特征值越大,该变量分布的范围越分散,在二元高斯分布中,对应特征值大的变量在函数投影图像中对应的是椭圆的长轴。高维的高斯分布情况可以按照这个规律进行推广。
2、多元相关变量高斯分布
当变量之间存在相关关系的时候,协方差矩阵不再是对角阵,而是一个对称的矩阵,矩阵的每个元素 σ i j 2 \sigma_{ij}^2 σij2表示变量 i , j i,j i,j的协方差。
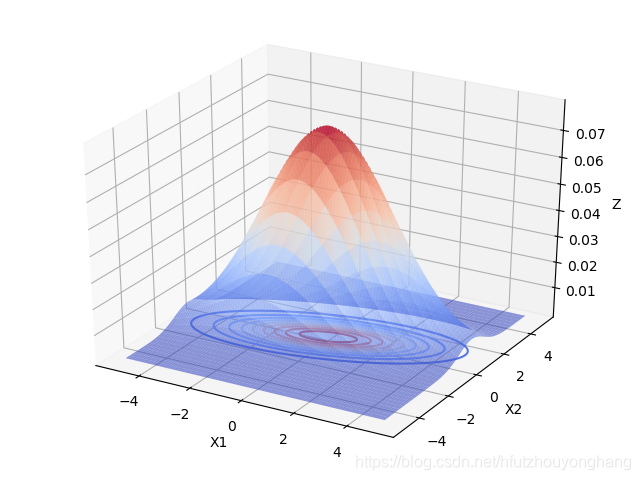
- 当 u = [ 0 , 0 ] Σ = [ 5 1 1 1 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}5&1 \\ 1&1\end{bmatrix} u=[0,0]Σ=[5111]时:
- 当 u = [ 0 , 0 ] Σ = [ 1 2 2 5 ] \boldsymbol u=[0,0] \boldsymbol\Sigma=\begin{bmatrix}1&2 \\ 2 &5\end{bmatrix} u=[0,0]Σ=[1225]时:
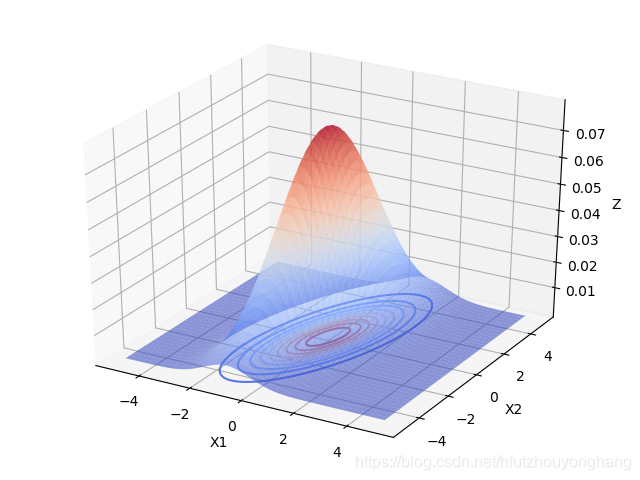
从上面2个图像中可以看出,变量之间具有相关关系时,与变量之间相互独立最大的区别是,投影面的椭圆长短轴不再平行与坐标轴。
 如果我们将坐标轴X1,X2旋转一下,与椭圆的长短轴平行,如下图所示:
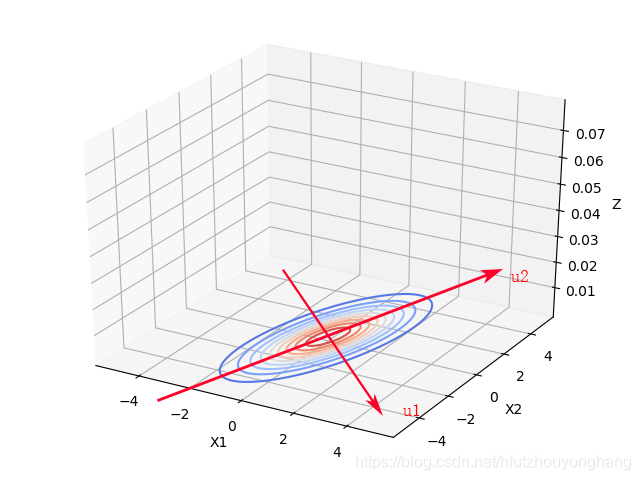
由独立变量的二元高斯分布知,那么在新的坐标系下, x 1 ′ , x 2 ′ x_1',x_2' x1′,x2′是相互独立的。上述过程称作为去相关性,这也是经典的降维方法主成分分析PCA的基础。以下是新坐标系的求解和原坐标系上的点在新坐标系下的坐标数学表达。
根据协方差矩阵的特征方程求解协方差矩阵的单位正交特征向量(先求出特征向量,再进行正交化与单位化),
Σ u i = λ i μ i \boldsymbol\Sigma u_i = \lambda_i\mu_i Σui=λiμi
假设上式中 μ i = [ u i 1 , u i 2 ] T \mu_i=[u_{i1},u_{i2}]^T μi=[ui1,ui2]T已经被单位正交化,以二维高斯分布为例
U = [ u 11 u 21 u 12 u 22 ] \boldsymbol U=\begin{bmatrix}u_{11}&u_{21} \\ u_{12} &u_{22}\end{bmatrix} U=[u11u12u21u22]
新坐标系的坐标轴为 μ 1 = [ u 11 , u 12 ] T \mu_1=[u_{11},u_{12}]^T μ1=[u11,u12]T, μ 2 = [ u 21 , u 22 ] T \mu_2=[u_{21},u_{22}]^T μ2=[u21,u22]T
新坐标系下,原坐标下下点的坐标为:
[ x 1 ′ x 2 ′ ] = U [ x 1 x 2 ] = [ u 11 u 21 u 12 u 22 ] [ x 1 x 2 ] \begin{bmatrix}x_1'\\x_2'\end{bmatrix} = \boldsymbol U\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}u_{11}&u_{21} \\ u_{12} &u_{22}\end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} [x1′x2′]=U[x1x2]=[u11u12u21u22][x1x2]
此时 x 1 ′ , x 2 ′ x_1',x_2' x1′,x2′之间没有相关关系。