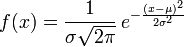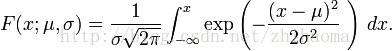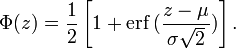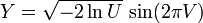转自：http://blog.csdn.net/rns521/article/details/6953591

正态分布（Normal distribution）又名高斯分布（Gaussian distribution），是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布，记为：X∼N(μ,σ²),

则其概率密度函数为：

正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布。

正态分布的定义

有几种不同的方法用来说明一个随机变量。最直观的方法是概率密度函数，这种方法能够表示随机变量每个取值有多大的可能性。累积分布函数是一种概率上更加清楚的方法，但是非专业人士看起来不直观（请看下边的例子）。还有一些其他的等价方法，例如cumulant、特征函数、动差生成函数以及cumulant-生成函数。这些方法中有一些对于理论工作非常有用，但是不够直观。请参考关于概率分布的讨论。

概率密度函数

正态分布的概率密度函数均值为μ 方差为σ² (或标准差σ)是高斯函数的一个实例：

下边是给出了不同参数的正态分布的函数图：

正态分布中一些值得注意的量：

 

• 密度函数关于平均值对称
• 平均值是它的众数（statistical mode）以及中位数（median）
• 函数曲线下68.268949%的面积在平均值左右的一个标准差范围内
• 95.449974%的面积在平均值左右两个标准差2σ的范围内
• 99.730020%的面积在平均值左右三个标准差3σ的范围内
• 99.993666%的面积在平均值左右四个标准差4σ的范围内
• 反曲点（inflection point）在离平均值的距离为标准差之处

 

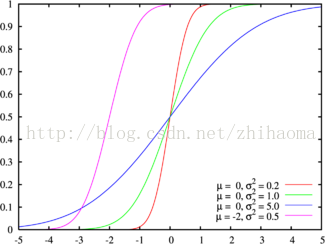
累积分布函数

累积分布函数是指随机变量X小于或等于x的概率，用密度函数表示为

正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示：

正态分布的一些性质 

1、如果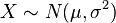且a与b是实数，那么aX+b ∼N(aμ+b,(aσ)²)

2、如果与是统计独立的正态分布随机变量，那么：

 

• 它们的和也满足正态分布
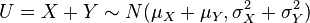
• 它们的差也满足正态分布
• U和V两者是相互独立的。

 

3、如果和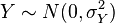是独立正态随机变量，那么：

 

• 它们的积XY服从概率密度函数为p的分布

 

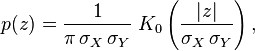其中K0是贝塞尔函数（modified Bessel function）

 

• 它们的比符合柯西分布，满足X / Y∼Cauchy(0,σX / σY)。

 

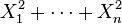4、为独立标准正态随机变量，那么服从自由度为n的卡方分布。

相关分布：

 

• R∼Rayleigh(σ)是瑞利分布，如果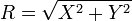，这里X∼N(0,σ2)和Y∼N(0,σ2)是两个独立正态分布。
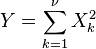• 是卡方分布具有ν自由度，如果这里Xk∼N(0,1)其中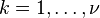是独立的。
• Y∼Cauchy(μ = 0,θ = 1)是柯西分布，如果Y = X1 / X2，其中X1∼N(0,1)并且X2∼N(0,1)是两个独立的正态分布。
• Y∼Log-N(μ,σ2)是对数正态分布如果Y = eX并且X∼N(μ,σ2).
• 与Lévy skew alpha-stable分布相关：如果因而.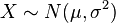
• 截断正态分布.如果， 在A以下和B以上截取X 将产生一个平均值这里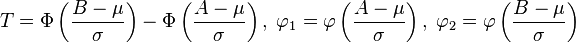，φ是一个标准正态随机变量的密度函数
• 如果X是一个正态分布的随机变量, Y = | X | ，那么Y具有折叠正态分布.