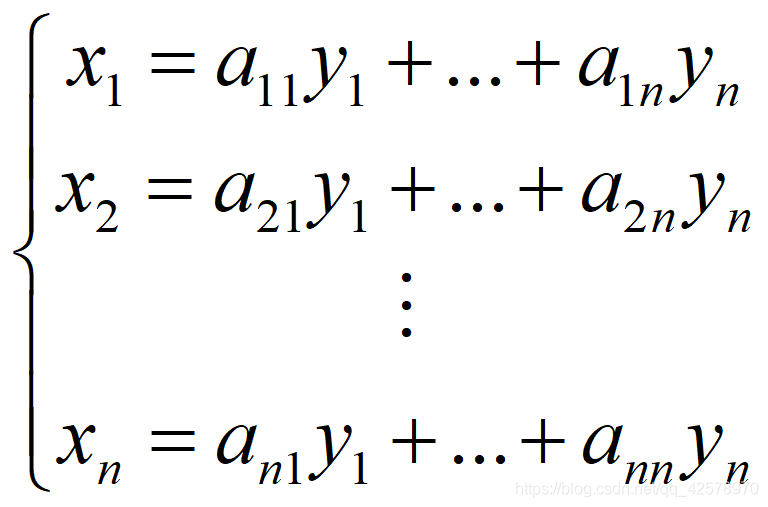二次型化为标准型

article/2025/10/2 18:34:09

将二次型化为标准形有利于我们了解二次型的简单形式、二次型的各种参数如正负惯性指数、得到二次型的规范形、对称矩阵合同的简单形等等。另外，化标准形也是解析几何化简二次曲线和二次曲面的需要。

下面，我们以两道题目为例说明计算二次型的标准形的2种方法：

配方法
正交变换法

配方法

在这里插入图片描述

其中

在这里插入图片描述

这里配方法有无数种配方的方法

正交变换法

在这里插入图片描述

这里提醒一下就是正交变换法的得到的矩阵只有一个就是特征值组成的矩阵

http://chatgpt.dhexx.cn/article/MyLeNDEx.shtml

二次型的标准型、规范型

若二次型只有平方项，则称二次型为标准型如果标准型中，系数只有1，-1和0，那么称为二次型的规范型，因为标准型中，1，-1，0的个数是由正负惯性指数决定的，而合同的矩阵正负惯…

二次型：含有n个变量 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn的二次齐次函数: f ( x 1 , x 2 , . . . x n ) a 11 x 1 2 a 12 x 1 x 2 a 13 x 1 x 3 a 14 x 1 x 4 . . . a 1 n x 1 x n f(x_1,x_2,...x_n)a_{11}x_1^2a_{12}x_1x_2a_{13}x_1x_3…

$二次型的正定$

二次型的正定

实数二次型的类型设为一个实二次型，若自变量不全为0 若恒成立，则称f为一个正定二次型，称A为正定矩阵若恒成立，则称f为一个半正定二次型，称A为半正定矩阵若恒成立，则称f为一个负定二次型&#xff0…

线性代数-二次型及其正定性

二次型及其矩阵表示形式二次型:含有n个变量的二次齐次多项式二次型矩阵:xTAx,其中A为实对称矩阵任给一个实二次型,就唯一确定一个实对称矩阵;反之,任给一个实对称矩阵,也可以唯一确认一个实二次型,因此,实二次型与实对称矩阵之间存在一一对应关系,称实对称矩阵A为二次型f的…

【考研线代】六. 二次型

文章目录第六章二次型6.1 二次型及其标准形6.1.1 概念6.1.2 合同基本性质6.1.3 题型 6.2 正定二次型6.2.1 概念6.2.2 定理 6.3 补充：解题技巧6.3.1 惯性定理的理解6.3.2 矩阵合同的充要条件6.3.3 配方法的坐标变换必须可逆6.3.4 正交变化化标准型 （&am…

线性代数（10）：二次型

一、二次型 （1）定义含有 n 个变量 x1，x2，…… ，xn 的二次齐次函数称为二次型； 对称矩阵 A 的秩也叫做二次型 f 的秩； （2） 例： 排列二次型所对应的矩阵 …

二次型化标准形的三种方法

二次型化标准形的三种方法将二次型化为标准形有利于我们了解二次型的简单形式、二次型的各种参数如正负惯性指数、得到二次型的规范形、对称矩阵合同的简单形等等。另外，化标准形也是解析几何化简二次曲线和二次曲面的需要。下面，我们以两道题目为例…

二次型化标准形的五种方法

文章目录 1. 配方法2. 初等变换法3. 正交变换法4. 偏导数法5. 顺序主子式法 1. 配方法用配方法化二次型为标准形的关键是消去交叉项，分如下两种情况： 情形1：如果二次型 f ( x 1 , x 2 , x 3 , ⋯ , x n ) {f \left( x\mathop{{}}\nolimits…