一、什么是TLSF算法

在嵌入式系统中，内存需要在分配和释放时有一个确定的相应时间，才能进一步分析其实时任务的可调度性。因此TLSF算法是一个十分适用嵌入式领域的动态内存分配算法。在关于TLSf算法的经典文章中《TLSF: a New Dynamic Memory Allocator for Real-Time Systems》详细介绍了TLSF算法相关知识。

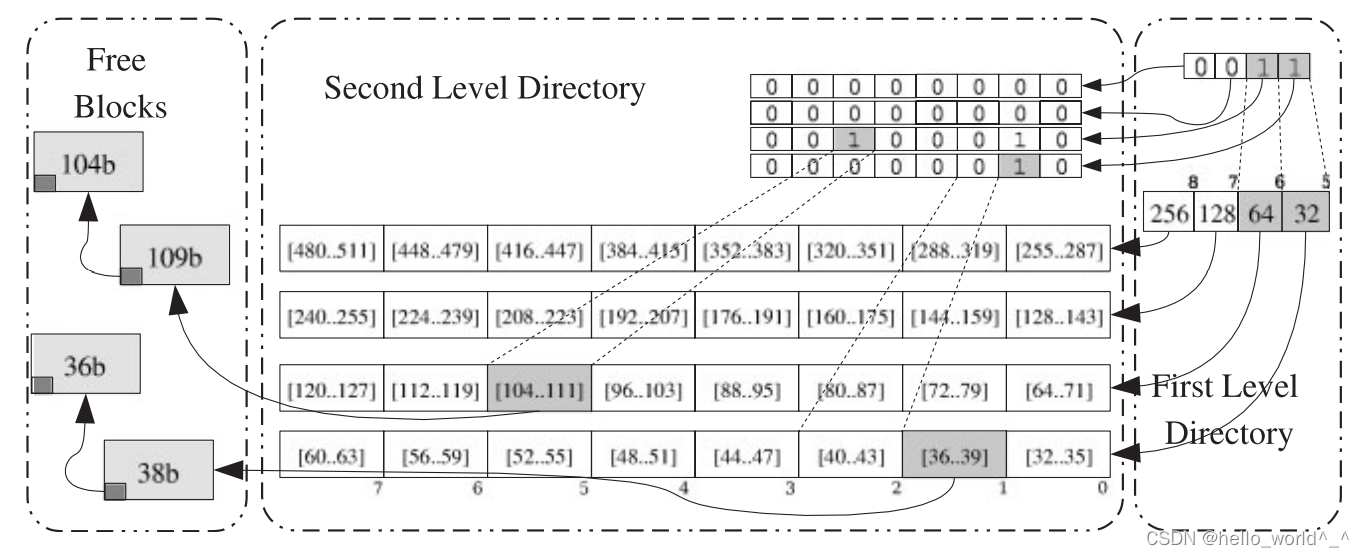
TLSF算法使用隔离匹配机制来实现良好匹配策略。基本的隔离匹配机制使用一组空闲列表，每个数组都包含一定大小范围内的空闲块。为了加快访问空闲块以及访问管理大量的隔离列表（以减少碎片），列表数组已组织为两个级别数组。一级数组将空闲块划分为类是2的幂（16、32、64、128等）；和第二级将每个第一级类别线性划分，划分的数量（简称第二级别索引数，2SLI）是用户可配置的参数。每个数组列表具有关联的位图，用于标记哪些列表是为空，哪些包含空闲块。每个块有关的信息都存储在块本身中。
TLSF空闲块的结构图
在TLSf的结构中，最主要的算法是位的操作，本文重点分析有关位的操作的原理与代码。当系统需要分配一个指定大小为r的内存时，需要计算出相应的两级位图的值，其公式如下所示：
计算公式
为了有一个直观的结果，我们假设SLI=4，即第二级索引将一级的内存块大小范围划分为2∧SLI=16块，则一级索引f=8，二级索引s=12。

二，f的确定

很显然，f的值就是所需内存大小的二进制位的最高非0位的数。首先最简单可以考虑到的就是从低位遍历即可，不断的对r进行”>>”操作，只要r不为0，就不断执行，同时定义一个变量统计移位的次数。但是因为是嵌入式系统，当然不能采用遍历的方法，会导致内存分配的不确定性。

方法一首先考虑折半查找的方式，32位的数字，折半对比5次既可求出f的值。代码参考如下：

int getF1(int r){int f = 0;if(!r){return 0;}if(r & 0xffff0000){r >>= 16;f += 16;}if(r & 0xff00){r >>= 8;f += 8;}if(r & 0xf0){r >>= 4; f += 4;}if(r & 12){r >>= 2; f += 2;