如何使用GeoServer发布地图
作者:郜庆科
本文所采用的系统为Windows 10 64bit操作系统,使用FireFox浏览器
一、安装配置Java的SDK
1、 安装Java Development Kit (JDK) 8,java开发环境,需要先到Java的官方网站下载合适自己的安装包,注意不要搞错自己系统类型,如果是32位系统请下载Windows X86,如果是64位系统如下:
2、 得到Java安装包一枚,一路默认下一步,一直到安装结束。
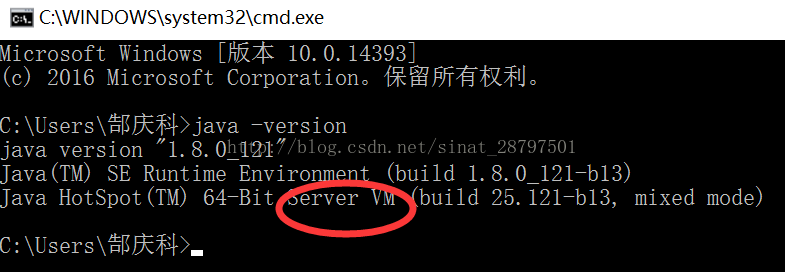
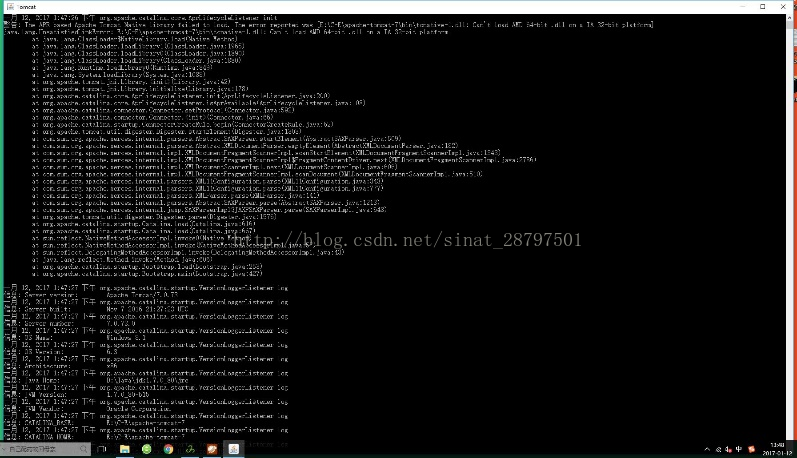
3、 验证是否安装Java成功,使用Win+R 运行cmd,进入命令行工具,运行“java –version”命令,注意这个命令中间有空格。得到如下结果即为安装成功:(注意此处一定是Server如果不是,那一定是版本安装错误了,去把Java卸载了,退回上一步找对版本安装)
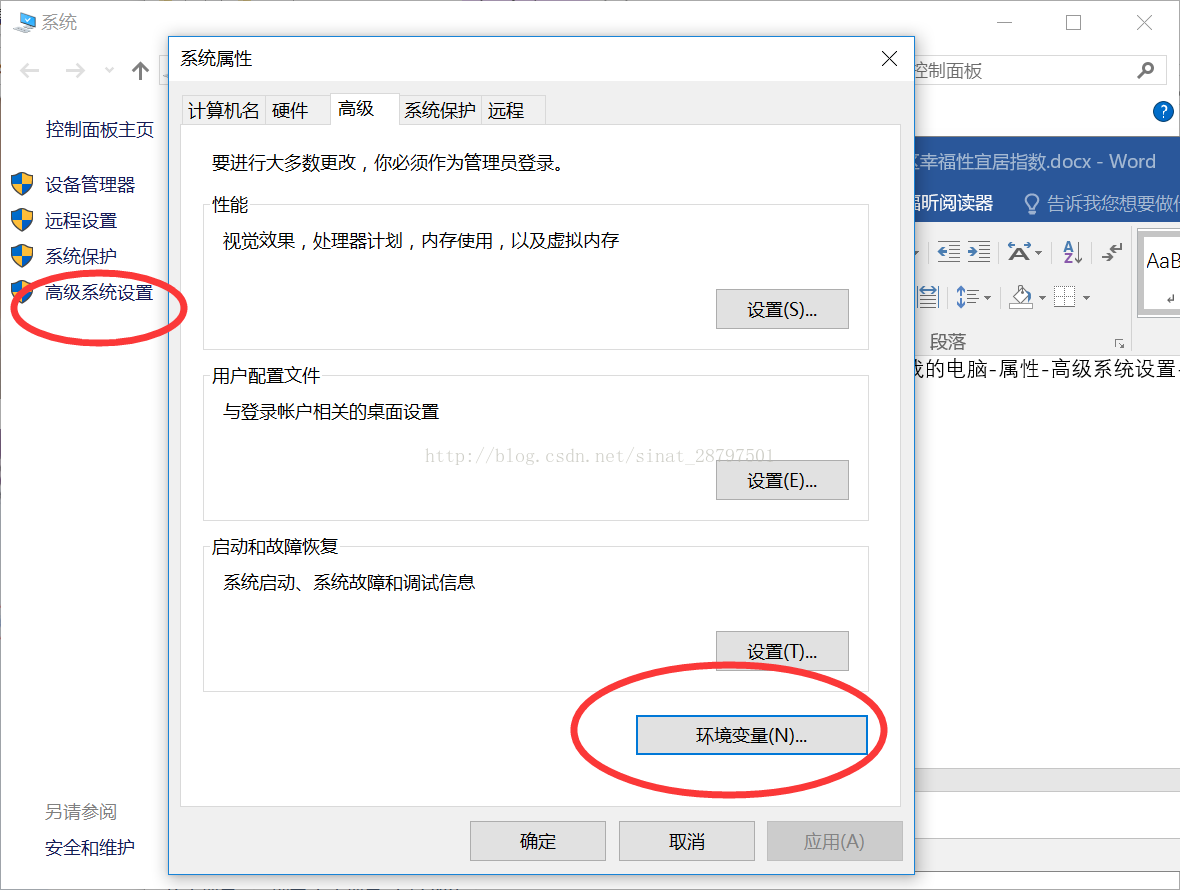
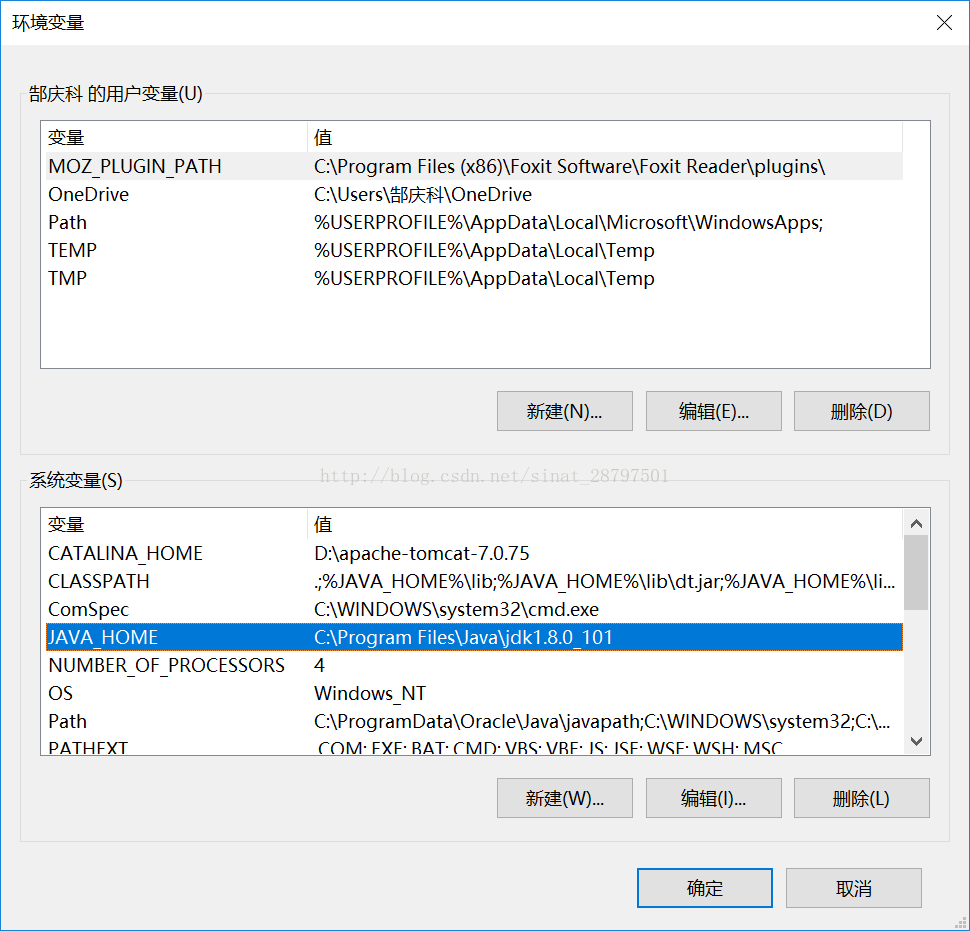
4、 接下来配置Java环境变量,右键我的电脑-属性-高级系统设置-系统变量-新建
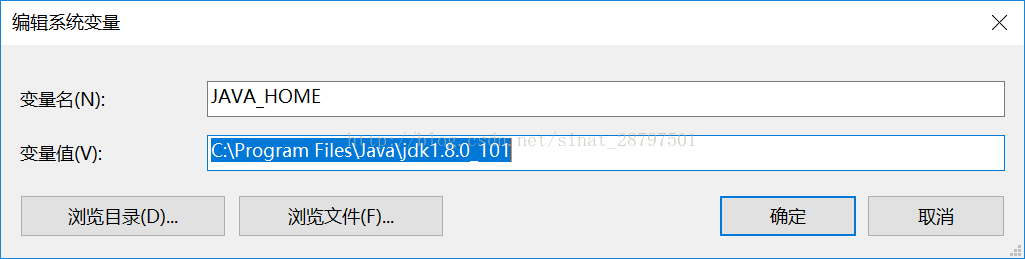
变量名:JAVA_HOME
变量值:(你安装Java的目录文件夹)我默认的,所以是C:\Program Files\Java\jdk1.8.0_101
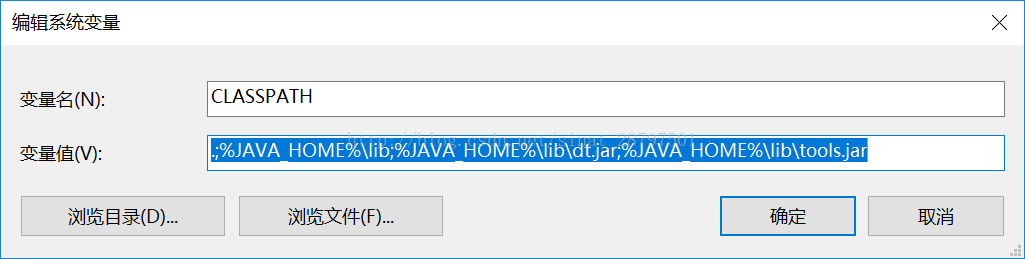
变量名:CLASSPATH
变量值:.;%JAVA_HOME%\lib;%JAVA_HOME%\lib\dt.jar;%JAVA_HOME%\lib\tools.jar
(注意前边有个点,分号,和百分号,别丢掉了)
双击path变量值-新建:%JAVA_HOME%\bin-确定
5、 到这里,java的环境就配置好了。
二、安装配置Tomcat
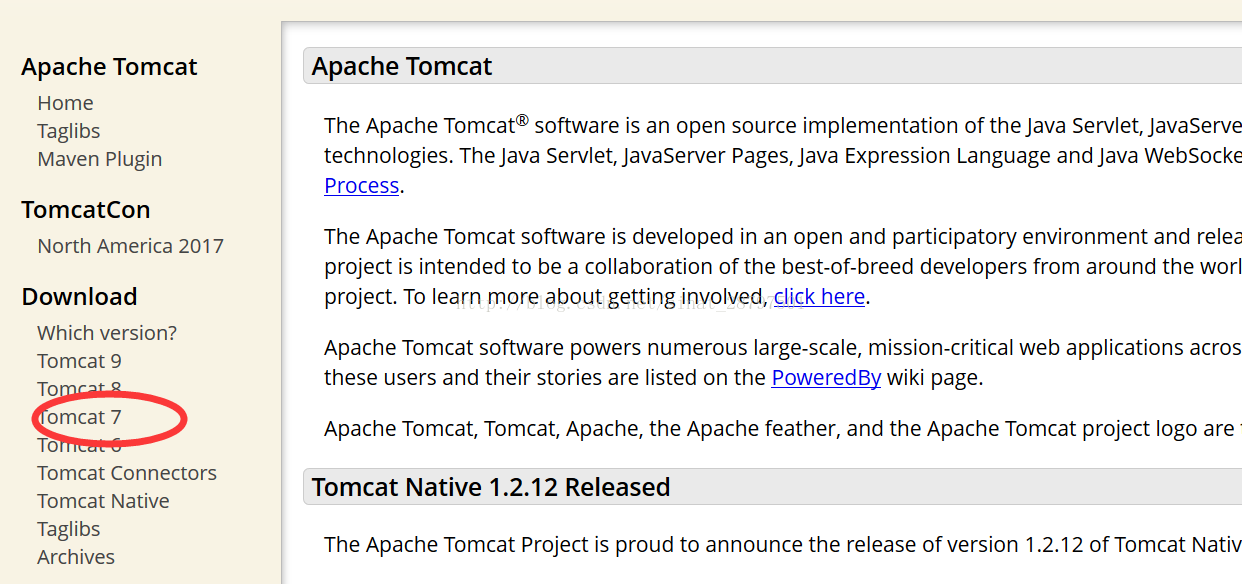
1、 到官网下载相应的安装包,并解压缩。
2、 把此解压后的文件夹放置在某个目录下,最好目录中不要携带中文,这里我放在了D盘的根目录下:
3、 首先跟刚才一样,在环境变量中添加环境变量CATALINA_HOME变量值为tomcat解压后的目录,我这里是D盘根目录:
4、
5、 进入tomcat的bin目录下,按住Shift+右键打,在此处打开命令行选项,开此目录下cmd,输入命令“service.bat install”,进行tomcat的服务安装,完成后,在命令行内执行命令“startup.bat”来启动tomcat服务。
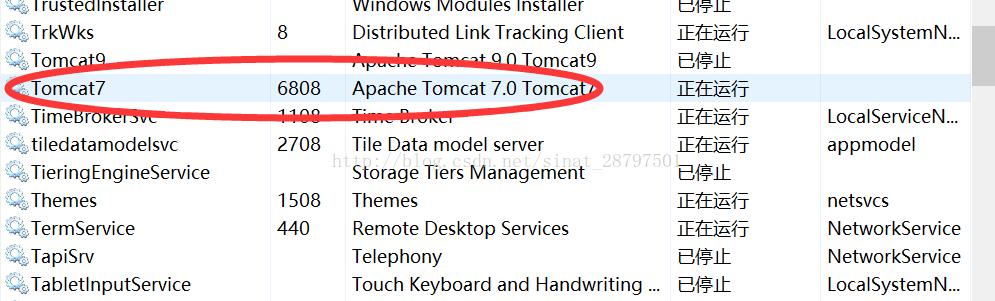
6、 接下来可以查看,是否运行了tomcat服务,右键任务栏-任务管理器-服务
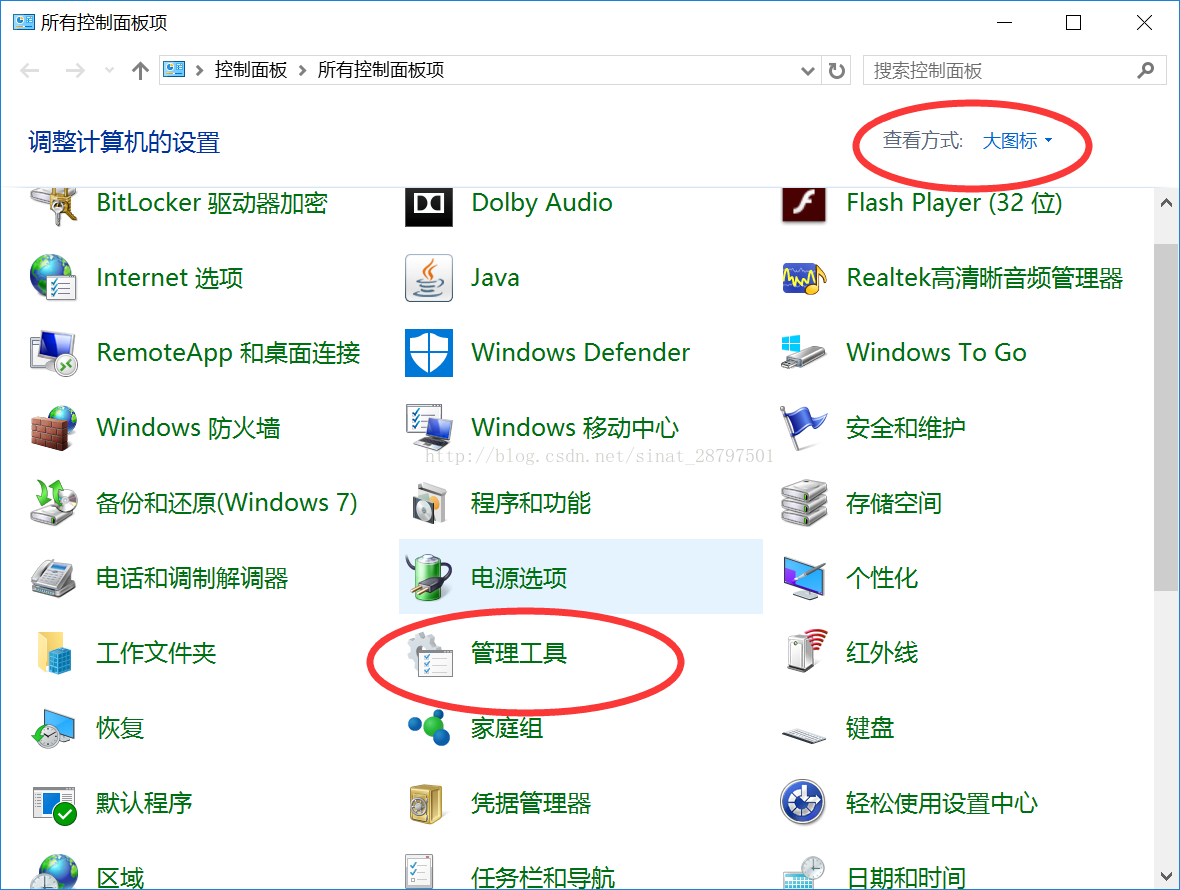
同时这里介绍一下如何关闭IIS,由于IIS使用的也是8080端口,所以可能会导致曾经使用过IIS的计算机无法使用tomcat,首先,进入控制面板。右上角查看方式-大图标-管理工具-服务-右键IIS关闭。
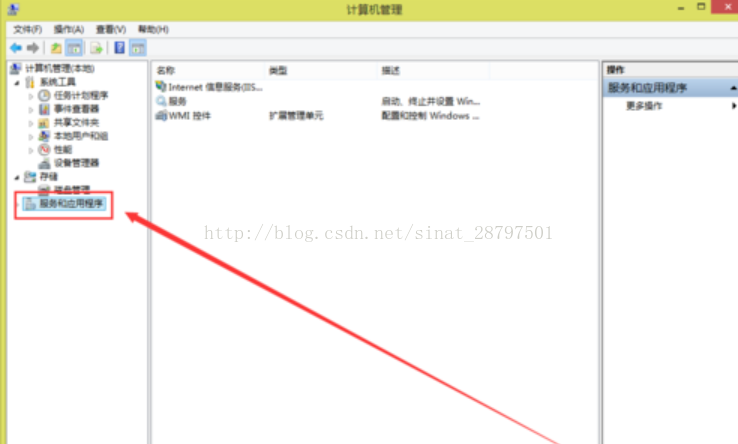
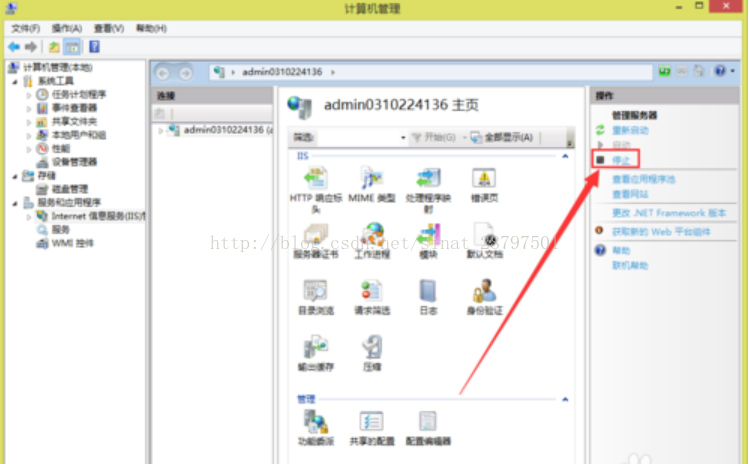
第二种方法是 我的电脑-右键管理-服务与应用程序-IIS管理器-右侧停止
7、 此时tomcat本地服务已经启动了,这时就可以使用浏览器进入网址:http://localhost:8080/进入tomcat的欢迎界面了,如下图:
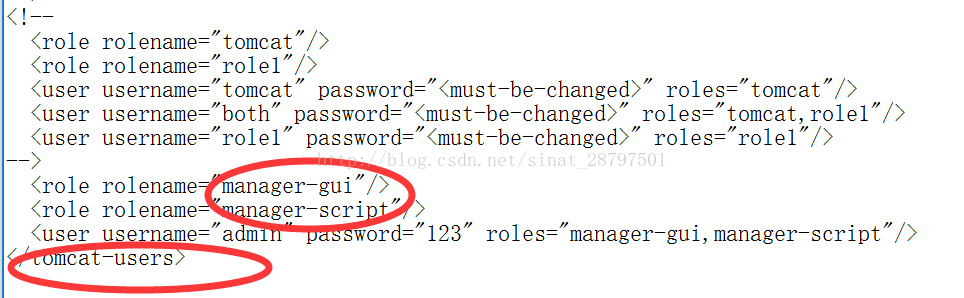
8、 由于我使用tomcat进行Web开发,所以这里需要修改tomcat的登陆账号和密码(点击欢迎页面的ManagerAPP时会让输入账号密码)。这里找到tomcat的根目录,进入conf目录下找到tomcat-users.xml文档,并使用文本文档进行编辑
这里一定要注意,在</tomcat-users>这个标签的前边重新写三行,这里的前两行的rolename按照上图不要修改,这个是tomcat认可的rolename,不要使用自己起的名字,同理,除了第三行username和password可以自己填写,其他的都不要变,后边的role对应上部的两个rolename。编辑完成后保存。
9、 这时再点击欢迎页面的ManagerAPP时会进入如下页面,这说明此时tomcat的账号密码设置好了,可进行之后的其他操作。(注意如果如果没有出现此页面的话尝试重启tomcat7服务,任务管理器-服务-tomcat7重启)
三、安装配置Geoserver
1、 首先、到geoserver的官网上下载,我这里为了方便,下载了War,如下图:
2、 下载完成后解压缩,得到war文件:
3、 此时进入tomcat目录下的webapps目录下,并将geoserver.war文件粘贴到此目录下
4、 此时,其实没有上图中的geoserver文件夹,这时,我们需要重启一下tomcat7服务,这样,tomcat会将war文件自动解压策划归纳为geoserver文件夹,具体过程不在贴图。
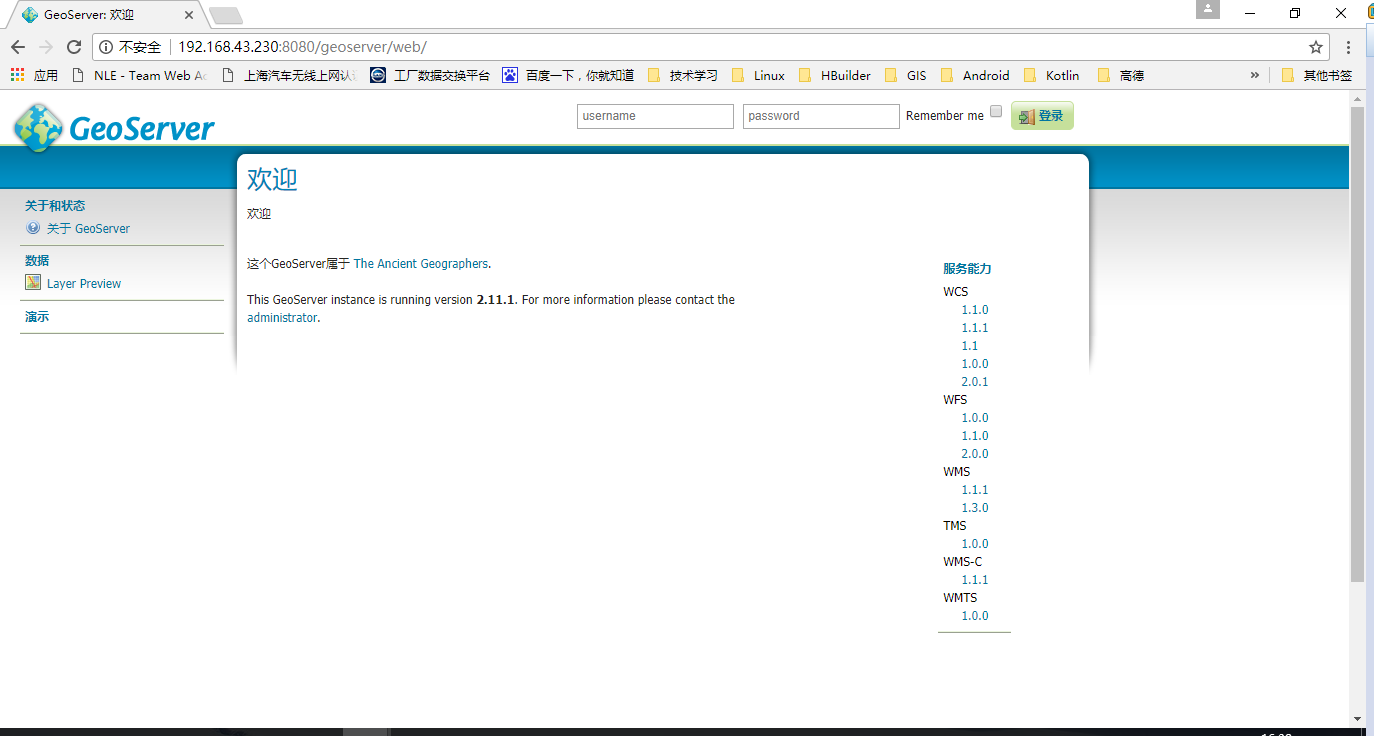
5、 进入浏览器输入网址:http://localhost:8080/geoserver/web/进入到GeoServer的欢迎界面如下所示,登陆自己的admin和geoserver的密码之后就可以进行地图的发布等服务了:
四、发布WMS
1、 首先把你需要发布的shp等文件的文件夹放在geoserver的data文件目录下,以方便之后的查找,GeoServer只能识别自己路径下的文件
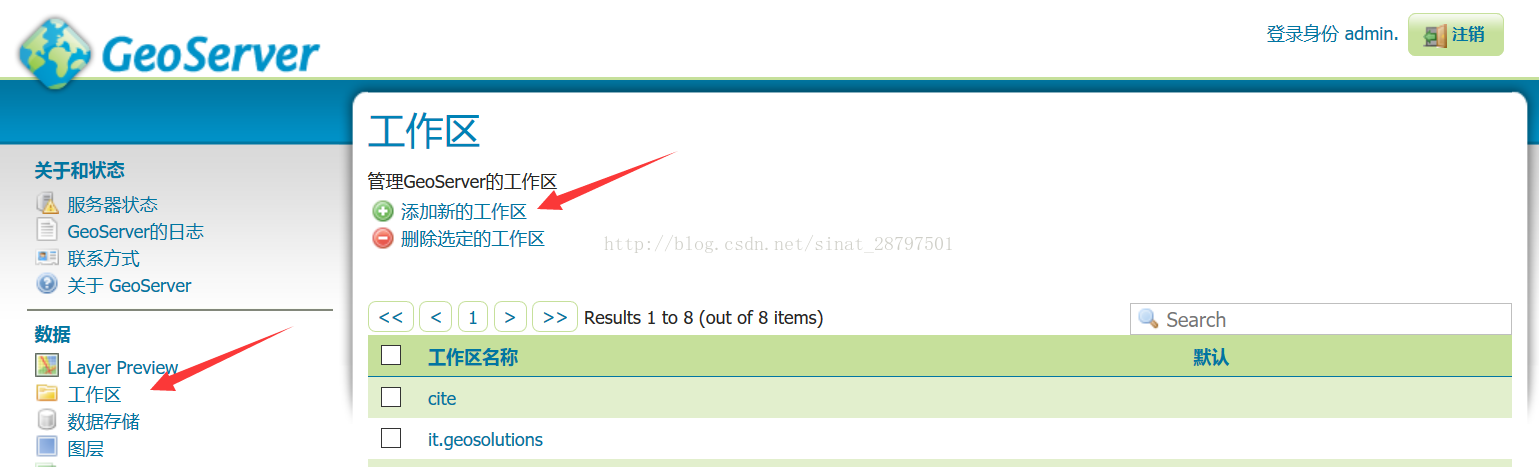
2、 接下来添加新的工作区
随便起一个名字,最好是英文,命名空间也是随便起一个,点击提交。
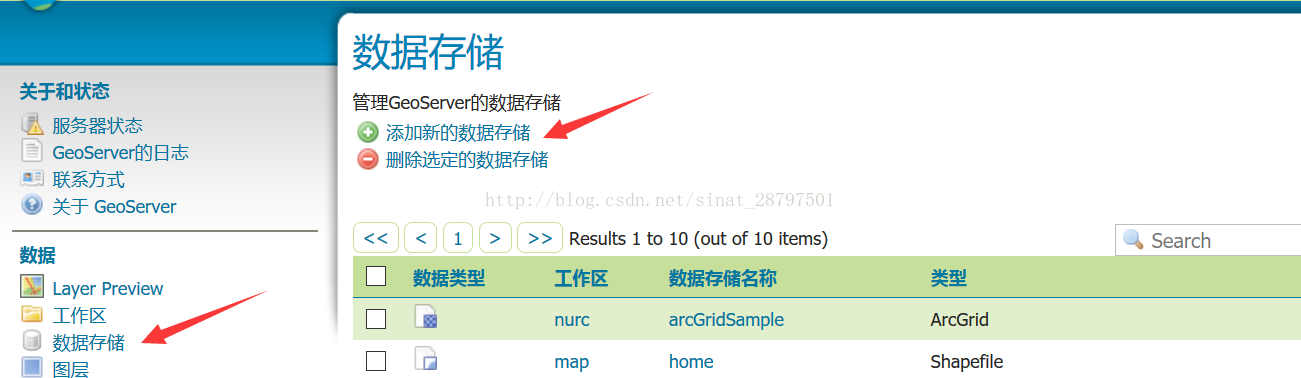
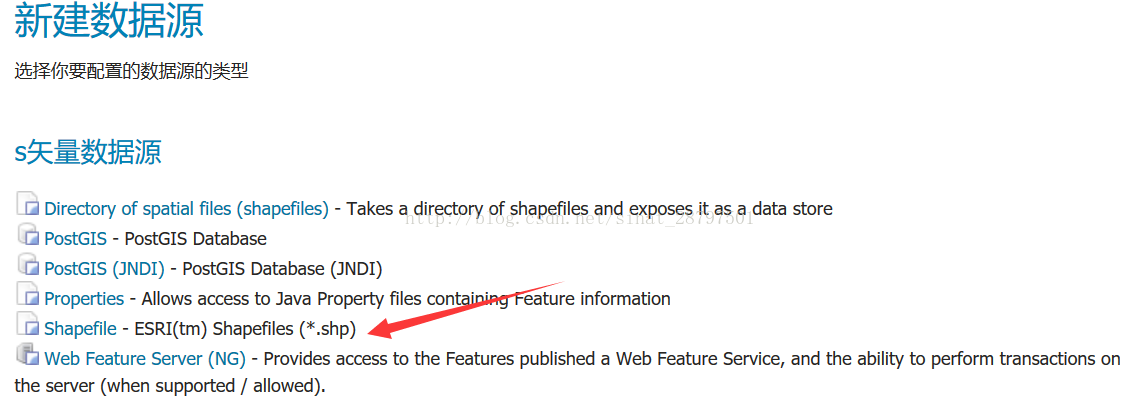
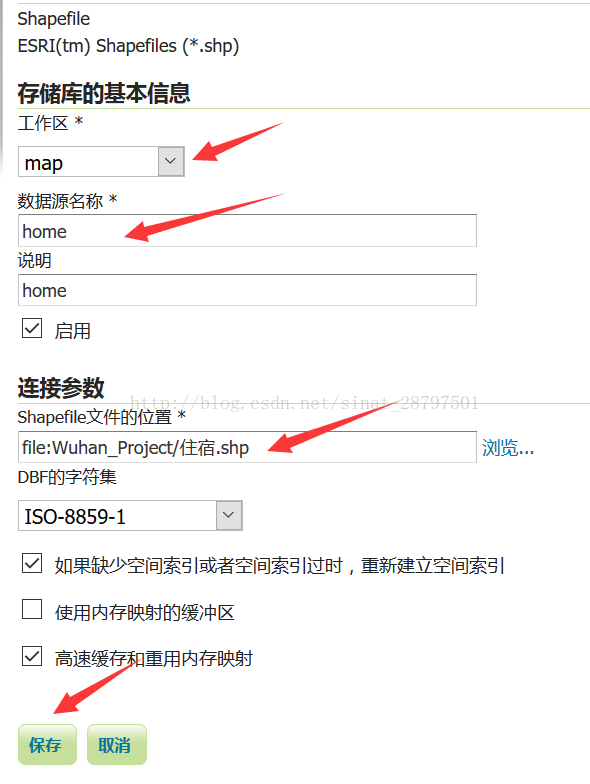
3、 新建数据存储,这里我们发布一个点要素的shp
找到相对应刚刚建立的工作区,填写数据源名称,最好是英文,填写文件位置,其他不要动保存。
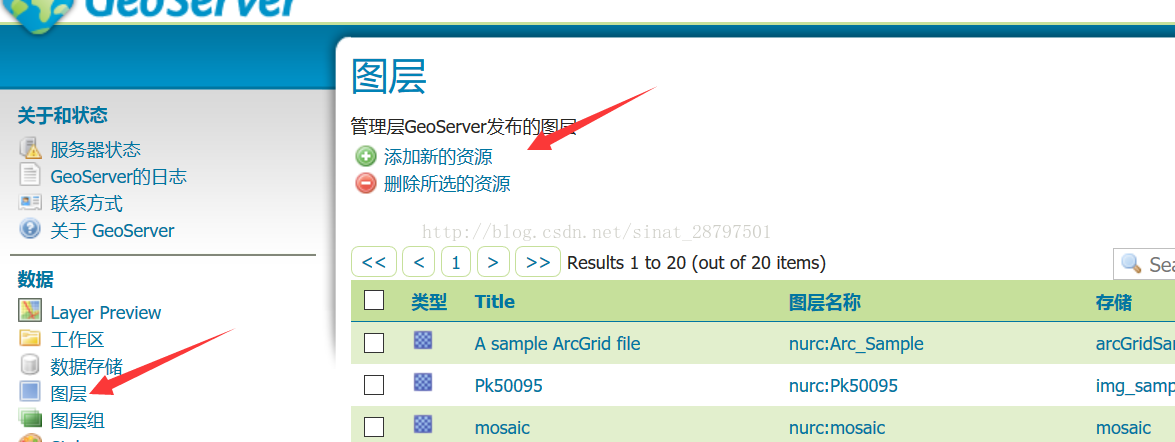
4、 然后进入图层中进行相应的图层发布
确认图层来源后点击发布
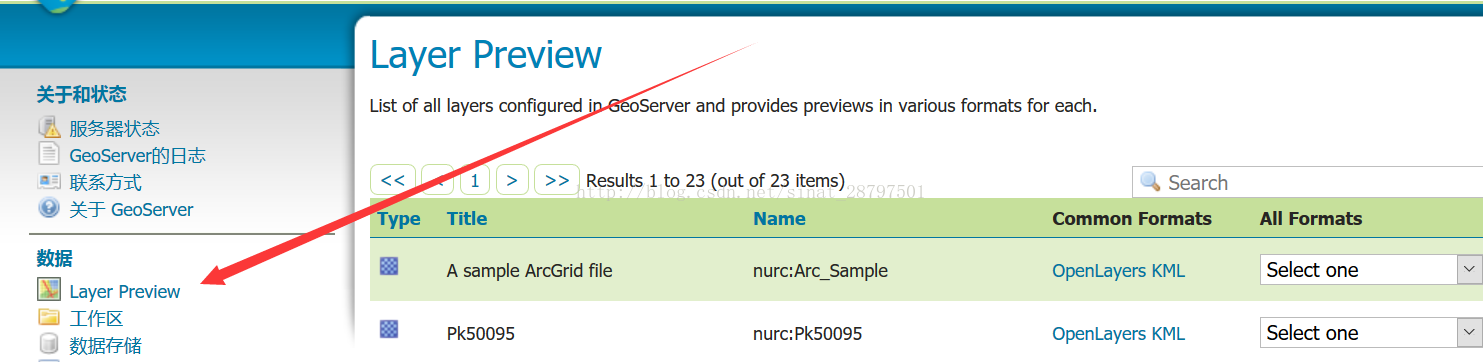
5、 此时已经发布好了这个图层,如果想看一下,可以进入Preview中
找到自己对应的刚刚发布的图层,可以用Openlayer打开也可以下载为KML或GML,用Open layer打开链接后点击要素可以进行查询(如果使用了Openlayer打不开链接,反而是下载了一个名为WMS的文件,那么很大原因是使用了中文名,如果不是的话就重新发布一次试一试)
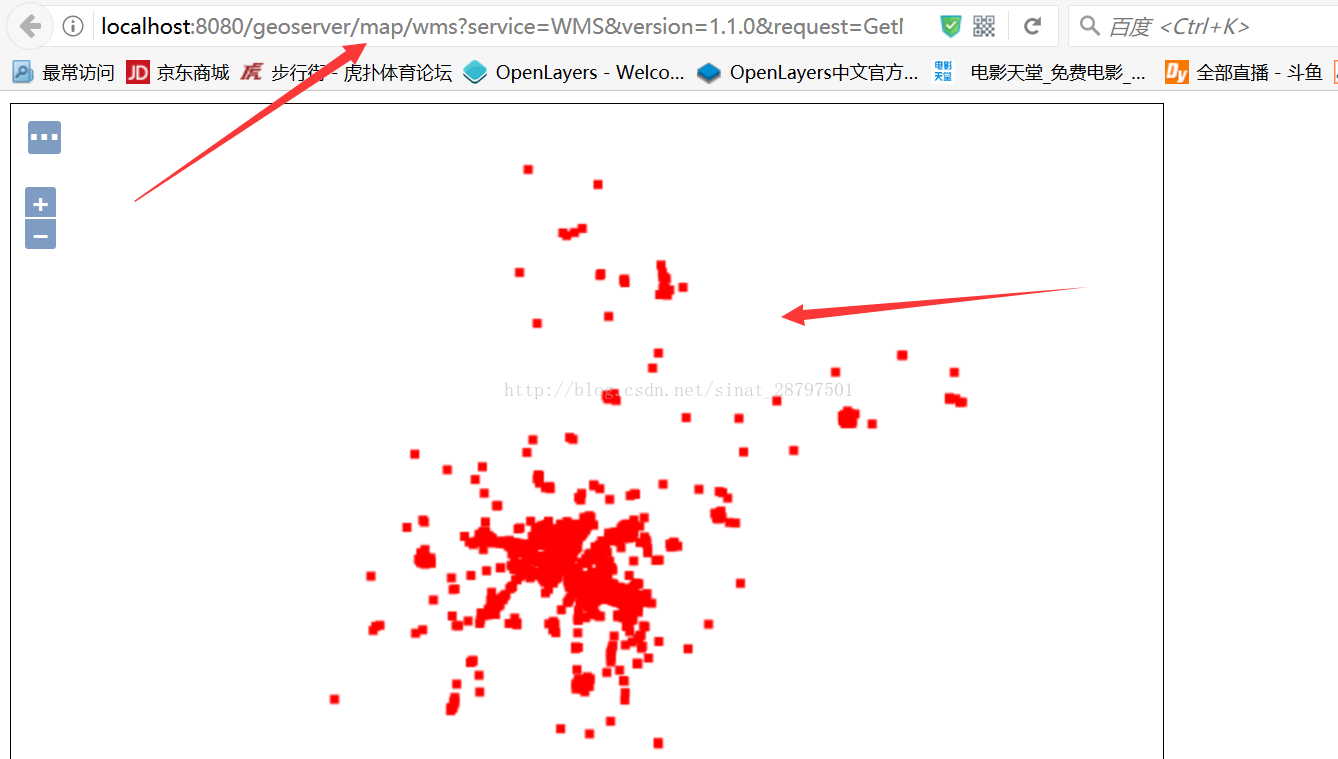
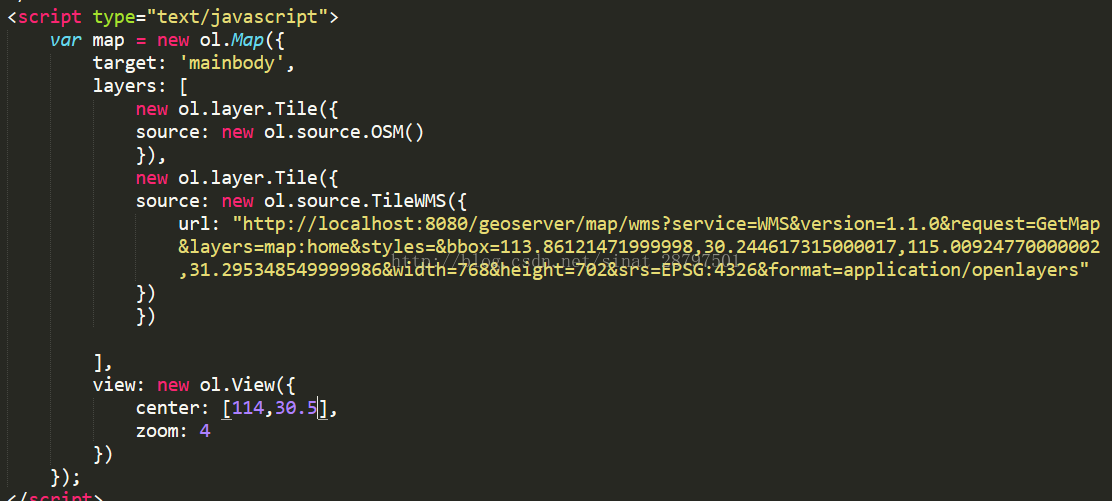
图层发布完成后,相应的链接就可以作为Open layer的layer中ol.souce.TileWMS的url了,具体调用如下所示:
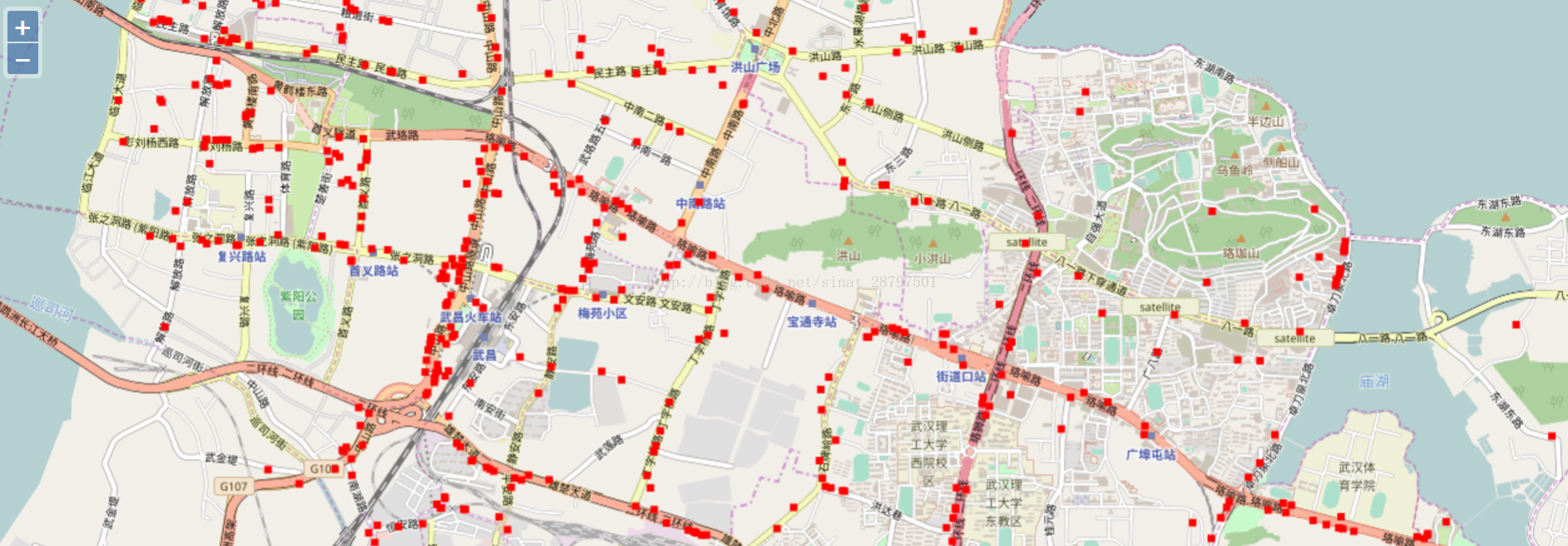
五、最终用浏览器打开我们的html文件,就可以看到刚刚加载的点了,这里我用了OSM作为底图(OpenStreetMap)