群论在物理学中的应用

article/2025/9/13 20:06:52

一、群论在固体物理中的应用

在我们本学期学习的《固体物理》这门课程中，已经广泛地提及和应用到群论的知识。固体物理的重点研究对象——晶体的原子排列具有极高的对称性，利用其结构上的对称性这一特性能够得到晶体的一些独特的物理特性。因此，用群论来描述这一对称性对于晶体结构及性质的研究有着十分大的作用。

1.基本思想

晶体中的原子排列具有极高的对称性。一般情况下，一个物体的对称操作数越多，其对称性越高。因此在固体物理中，引入了对称操作群及点群、平移群、空间群等来描述晶体的对称性，进而研究晶体的物理性质。

2.具体例子

（1）对称操作群
根据群的概念，定义一个物体全部对称操作的集合为其对称操作群。
此时，群概念中的“乘法运算法则”为“连续对称操作”，“单位元素”为“不动操作”，“绕轴转θ角的逆”为“绕同样的轴转-θ角”，“中心反演”的逆还是“中心反演”；此外，两个操作A和B的“乘法”结果为另一对称操作C同样在该对称操作群中。
利用对称操作群的概念，可以推导出具有某一对称性的晶体的介电性ε的特殊形式。
（2）点群
点群是描述晶体旋转对称性的对称操作群。
晶体的宏观对称性是在晶体原子的周期排列基础上产生的，一个重要的后果是宏观对称性可能有的对称操作受到严格限制。已被证明知，不论任何晶体，它的宏观对称性只可能有下列10种对称素：

在以上10种对称素的基础上组成的对称操作群称为点群。且有具体的分析可以证明，由十种对陈素只能组成32各不同的点群。这就是说，晶体的宏观对称性只由32个不同类型，分别有32个点群来概括。这32个点群有回转群、双面群等。
（3）平移群
晶体的周期性，也称为平移对称性，可以用布拉伐格子来表征，平移一个布拉伐格子的晶格矢量

晶体与自身重合，称为平移对称操作。所有布拉伐格子晶格矢量所对应的平移对称操作的集合，称为平移群。对于无限大的布拉伐格子，平移群是无限群。
（4）空间群
前面已经提到，点群是描述晶体旋转对称性的群，平移群是描述晶体平移对称性的群。而晶格全部对称操作（即有平移也有转动）的集合，构成空间群。
空间群分为两类：一类是简单空间群或称点空间群；一类称为复杂空间群或称非点空间群。
点空间群是有一个平移群和一个点群对称操作组合而成的，简单晶格和原胞中各原子性质互不相同的复式晶格所具有的空间群都属于点空间群，例如NaCl和ZnS晶体；复杂空间群是具有螺旋轴和滑移面这两种特有对称操作的对称操作群，复式晶格中如有性质相同的原子，它们的空间群有时是复杂空间群，例如金刚石晶体。

二、群论在量子力学中的应用

1.基本思想

量子力学的基本问题是研究薛定谔方程的解：
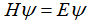
在这里插入图片描述
但是，除了在极少数简单情况外，一般情况很难得到E及Ψ的精确解。群论的方法可以通过找出哈密顿量H的对称性，预测能量E的简并情况。这便是群论在量子力学中的一种应用。
下面将简单讨论群论在量子力学中的具体应用实例。

2.具体例子

（1）氢原子能级偶然简并的解释
由量子力学的薛定谔方程求解得到某一确定能级对于若干态矢量（或波函数），这种多个态矢量处于一个能级的现象称为“简并”。它表明原子的哈密顿量具有某种对称性。因原子核的库仑势具有球对称性，故一般多电子原子态矢量由三个量子数n、l、m描述（不计自旋）。能级E（n、l）与量子数n、l有关简并度是2(l+1)；但是，对于氢原子（或类氢原子）同样情况简并度却高得多
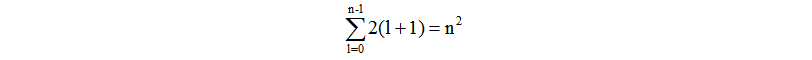
在这里插入图片描述
氢原子的简并度高于一般原子的现象，成为“偶然简并”。传统量子力学除了说明量子数的意义之外，无法解释偶然简并现象。
随着群论的引入，偶然简并现象得到正确的解释。群伦指出：多电子原子其哈密顿仅具球对称性，属于SO(3)群；氢原子（及类氢原子）哈密顿量除了几何对称性之外，还有更高的对称性（即內禀对称性），属于SO(4)群，故其简并度高于一般多电子原子。
（2）原子能级在晶体场中的分裂
群论方法可以通过找出哈密顿H的对称性，预测能量E简并情况。在单电子近似下，哈密顿H形式为：
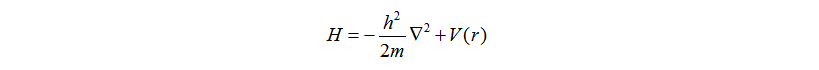
在这里插入图片描述
对于自由原子，势能项V®具有球对称性。在三维旋转群算符PR作用下具有不变性

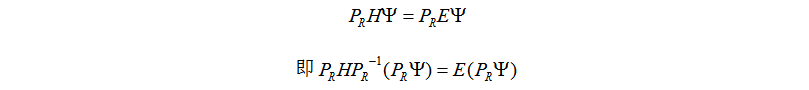
令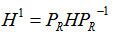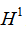，是坐标变换后的哈密顿算符。上式说明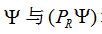均是哈密顿的本证函数，具有相同的能量本征值E0，我们称使体系保持H不变的群为体系哈密顿所属的群。即若令G={PR}。则G即是哈密顿H所属的群。
若将原子放置在具有某种对称性的晶格中，称原子处在晶体场中。由于晶格点阵对原子作用，使原子的哈密顿函数出现微扰变化。从群论观点看，自由原子的H0所属的群是G群（通常是SO(3)群），围绕能V所属的若为S群。因为晶体场的微扰作用使对称性缩小（由球对称得到某种晶体点群对称）。所以比较而言，G为大群，S为G的子群。群伦指出，大群G的不可约表示代表一条新分裂的能级。在群论中称为“分岐率”。若群G=SO(3)群，不可约表示D(L)代表能量本征值E(nl)，且是(2l+1)维简并。则D(L)对子群S，一般来说是可约化的。设D(L)被群S约化为K个不可约表示{D1(L)、D2(L)……DK(L)}，表明自由原子能级在晶体中分裂为K条。