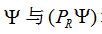1. 简述李群的定义
群论讲解步骤:群→连续群→拓扑群→李群
李群是具有某种性质的拓扑群,一句话总结就是:
若群参数连续且无限阶可微的群称为李群。
用流形的语言描述就是:
李群简单地说就是具有群结构的微分流形。
想了解李群的详细定义,需要先了解拓扑、流形、拓扑流形、微分流形的定义,目前暂时不细细展开,后面再谈。所以这章主要介绍部分经典李群
2. 几种经典李群
例1  群
群
一般线性(general lineaer)群,又称矩阵群,指对n维矩阵做线性变换。
n维矩阵的GL群,GL(n)的参数量是n^2个。
例2  群
群
所有单位复数构成的集合是一个李群,即
U(1)群就是前面提到的经典的复数旋转群(或二维旋转群)
例3  群
群
S指Special,即行列式为1;O指orthogonal,即标准正交的;2指维度为2(不是指参数个数)。

:连续,无限阶可微,
SO(2)群描述二维转动,所以又叫(定)轴转动群。
例4 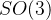 群
群
SO(3)描述三维转动,需要三个角度参数,其中两个角度参数描述旋转轴,剩下一个描述旋转角度。
例5  群
群
U指unitary,单位或归一,指矩阵乘以自身共轭转置为单位矩阵。
SU(2)由三个参数表示,具体为:

其意义我们将在后面和四元数一起讲
结论是:SO(2)和U(1)等价,SO(3)和SU(2)等价