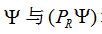离散数学中群的概念

群的定义

说起群，首先要引出一个更大的概念——代数系统（什么是代数系统就不解释了…），其中在概念上来看，代数系统>广群>半群独异点>群。

设【<G,*>】是一个代数系统，其中G是一个集合，*是一个任意的二元运算符：

• 若满足*运算在G中封闭（对于所有G中a和b，运算a.b的结果也在G中），则代数系统【<G,*>】是广群。

• 在广群的基础上，如果【<G,*>】符合以下性质，则是半群：

  结合律：对于所有G中的a和b和c，等式(a.b)·c=a·(b·c)成立。

• 在半群的基础上，如果【<G,*>】符合以下性质，则是独异点（幺半群）：

  存在单位元（幺元）：存在G中的一个元素e，使得对于所有G中的元素a，总有等式e·a=a·e=a成立(类似于乘法中的1和加法中的0)。

• 在独异点的基础上，如果【<G,*>】符合以下性质，则是群。

  存在逆元：对于每个G中的元素a，存在G中的一个元素b使得总有a·b=b·a=e，此处e为单位元（类似乘法中的6和1/6，加法中的6和-6）。

综上，若一个代数系统【<G,*>】

• 运算*是封闭的

• 运算*是可结合的

• 存在幺元e

• 对于每一个元素x存在这它的逆元

则称<G,*>是一个群。

举例

【整数乘法】就只是一个半群，而不是群，因为他不能保证每一个元素都有逆元（6和1/6，但是1/6并不是整数）

但值得一说的是【实数乘法】也不是群，仅仅是因为0没有单位元（幺元）。

几种常见的群

1. 交换群（阿贝尔群）：

   群运算的次序很重要，把元素a与元素b结合，所得到的结果不一定与把元素b与元素a结合相同（比如说矩阵乘法）；即满足交换律的群称为交换群，不满足交换律的群称为非交换群（非阿贝尔群）

2. 循环群：

   群G自身便是它的一个生成元集，是能由单个元素所生成的群。

   

   例如<2,4,8,16…>

3. 对称群：

   它的元素是所有X到X自身的双射，设X是一个集合（可以是无限集），X上的一个双射（既是单射又是满射）：a:X→X（即是置换）。集合X上的所有置换构成的族记为S(x)，S(x)关于映射的复合运算构成了一个群，当X是有限集时，设X中的元素个数为n，则称，群S(x)为n次对称群。（备注，对称群的数学定义还是没有完全弄懂，从图形上来讲，可能类似于正方形的旋转和反射操作）

4. 置换群：

   

   n元对称群的任意一个子群，都叫做一个n元置换群，简称置换群。

5. 李群

   指具有群结构的光滑微分流形，其群作用与微分结构相容。李群是连续的群，也即其元素可由几个实参数描述。因此，李群为连续对称性的概念提供了一个自然的模型，例如三维旋转对称性。李群被广泛应用于现代数学和物理学。（李群没搞懂…姑且先粘上定义吧…）

群的由来

群的概念产生自多项式方程的研究（简单说就是为了解多次方程）：

1. 古巴比伦数学和印度数学中，人们能够用根式求解一元二次方程（什么是根式解，见下面的补充）。

2. 接着古希腊人和古东方人又解决了某些特殊的三次数字方程，但没有得到三次方程的一般解法（这个问题直到文艺复兴的极盛期才由意大利人解决）。

3. 文艺复兴时期，意大利人费尔拉里又求解出一般四次方程x^4+ax^3+bx^2+cx+d=0的根是由系数的函数开四次方所得。

1. 在以后的几个世纪里，探寻五次和五次以上方程的一般公式解法却一直没有得到结果。

2. 1770年前后，法国数学家拉格朗日提出【方程根的排列与置换理论】是解代数方程的关键所在，促进了代数方程论的进步。但是这种方法却不能对一般五次方程作根式解。

3. 随后，挪威数学家阿贝尔证明了一元二次，三次和四次方程都有求根公式，但是一般的五次方程却无求根公式，并给出了【高于四次的一般代数方程没有一般形式的代数解】的证明。阿贝尔解决了构造任意次数的代数可解的方程的问题，并且在研究中已经涉及到了群的一些思想，只是阿贝尔没能意识到。

4. 法国数学家伽罗瓦在这样的背景下，提出了群的概念，用群的理论彻底解决了根式求解代数方程的问题。

补充

根式解：如果一个方程的系数经过有限次的加、减、乘、除以及开整数次方等运算表示出来，就称为这个方程存在根式解。

比如

就是二次方程的根式解。

一、二、三次代数方程都有根式解。

群能解决什么问题（行业应用）

1. 化学：

   从群论中的Burnside引理出发，得到的波利亚计数公式对组合计数非常有用，常用于分析化学上的同分异构体。

2. 材料学：

   晶粒作为陶瓷材料的单元，因此，对晶粒的研究可得到获得新的材料性能的思路。通过对这些具有一定力学性能、物理性能的材料的微观本质的分析，可以反过来利用对称群分析看看可以通过如掺杂等哪些方式来改变晶体的晶格以获得性能更佳、物理效应更显著的晶体。

3. 图论：

   求解不同构的图的数目，项链问题，染色问题等等。

4. Lie 群在机械中的应用：

   李群的概念在微分方程和流形中都有很重要的角色，其结合了群论和分析数学，能很好的描述分析数学结构中的对称性。对这类群的分析又叫调和分析。在机器人的控制，最优控制、参数优化中均有作用。

5. 基础物理：

   群论提供了特殊的表, 称为字符表,
   用来预测分子的对称性对其振动模式和其他重要性质的影响。

6. 用群论研究纠错码（通信理论，数据传输、密码学）

7. 在组合数学中，交换群和群作用常用来简化在某些集合内的元素的计算。

8. 后来群论广泛应用于各个科学领域。凡是有对称性出现的地方，就会有它的影子，例如物理学的超弦理论。

交换群和群作用常用来简化在某些集合内的元素的计算。

8. 后来群论广泛应用于各个科学领域。凡是有对称性出现的地方，就会有它的影子，例如物理学的超弦理论。