本章主要讲述如何下载和安装使用GeoServer服务器,介绍了GeoServer的管理界面,并演示了发布地理数据的简单流程。
主要从以下几个方面展开叙述:
- 下载和安装GeoServer
- GeoServer管理界面
- 发布图层数据的流程
1. 下载和安装GeoServer
GeoServer是一个共享地理空间数据的开源服务器,为提空间数据的交互性而设计,可以使用开放标准发布主流的空间数据源。GeoServer实现了行业标准的OGC协议,如Web属性服务(WFS)、Web地图服务(WMS)和Web覆盖物服务(WCS),以及可选的Web处理服务(WPS)和Web地图瓦片服务(WMTS)等。其官方网站为:
http://www.geoserver.org/,
GeoServer有两种运行方式,可以作为独立程序单独运行,也可以以war包的形式部署在Web应用服务器中运行。本文使用war包部署方式运行,所用的GeoServer版本号为2.20.1,下载地址为:
https://sourceforge.net/projects/geoserver/files/GeoServer/2.20.1/geoserver-2.20.1-war.zip
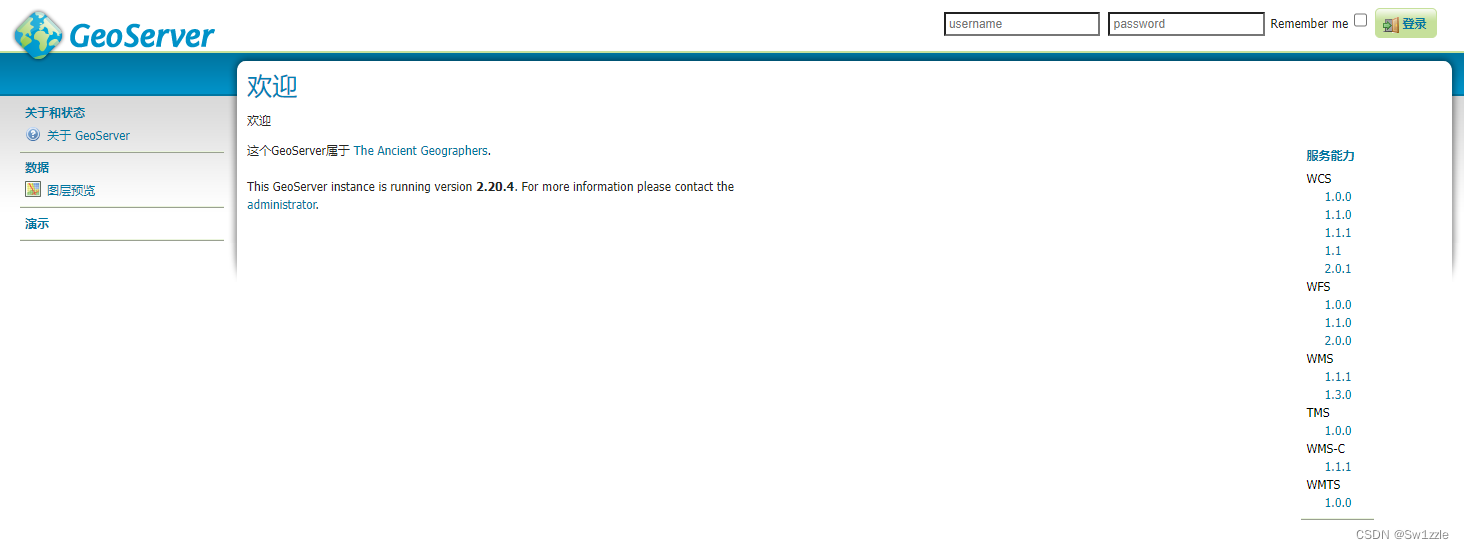
将下载回来的war包放到Tomcat服务器的Webapps文件夹下,Tomcat就会自动部署该应用,打开浏览器,输入访问地址 http://localhost:8080/geoserver,可看到如下管理界面:

2. GeoServer管理界面
输入默认的用户名admin,密码geoserver即可进入管理界面了。

每次进入管理界面都会显示欢迎界面,欢迎界面中会显示当前共有多少个工作区、数据存储和图层,并提示为了安全请及时修改master和admin的默认密码。
管理界面左侧为功能菜单,右部为工作区。功能菜单分为“数据”“服务”“设置”“瓦片缓存”“安全”等几个栏目,每个本项目中包含多个功能选项,点击每个功能选项会在右侧的工作区显示该功能的简单描述和具体内容,可挨个点击以熟悉管理界面的功能。
3.发布图层数据的流程
“数据”栏主要用来进行图层数据的发布。在GeoServer中,使用工作区、数据存储和图层共三级结构来组织管理地理空间数据,发布一个地理空间数据基本上也是按照这个顺序进行操作。准备好数据源,我们要开始了。
(1)新建工作区
工作区相当于一个命名空间,用于组织一系列数据的存储,可以为这些数据存储进行统一管理,并分配统一的安全权限。点击“新建工作区”按钮即可打开“新建工作区”界面如下:

在这个界面中给工作区起一个有意义的名字,并输入一个URI作为命名空间与这个工作区相关联,也可在“Security”标签页中进行安全设置,然后点“保存”就可以创建这个新工作区了。
(2)新建数据源
一个工作区下可以创建多个数据源,数据源是真正存储地理空间数据的地方,点击“添加新的数据存储”就可以打开“新建数据源”页面。

在“新建数据源”页面中,可以看到GeoServer可以支持矢量数据源、栅格数据源和其他数据源,每种类别下都有很多常见的主流地理空间数据格式。其中GeoTIFF(Tagged Image File Format with Geographic information)的数据源最通用也最易获得,所以这里就以GeoTIFF格式为例演示如何创建新的数据源。
在“栅格数据源”类别下点击“GeoTIFF”即可进入“添加栅格数据源”页面。

在这个页面中,首先选择前面创建的工作区,然后为数据源起一个容易识别的名字。“连接参数”处的URL为数据源文件的存储位置,此处可选择提前准备好的GeoTIFF格式的文件,一定要保证Tomcat具有读取这个文件的权限,否则会导致访问失败。最后选中“启用”并点击“保存”按钮,数据源就算创建成功了。
(3)新建和编辑图层
通常,在第(2)步点击“保存”按钮后,会自动跳转到“新图层”界面,此时直接点“发布”就可以添加新图层了。

如果没有跳转到“新图层”页面,则需要点击“添加新的资源”来进入“新建图层”页面了。
此时选择第(2)步中创建的数据源,下面会自动显示出可发布的图层名称和“发布”按钮,如果这个图层以前发布过,就会出现“再次发布”的字样,点击“发布”会打开“编辑图层”页面。

在这里简单的设置一下图层的名称,如果所选中的GeoTIFF文件中包含有坐标参考系统和边界框信息,就会自动填充在下面的输入框里,否则的话就需要手工填写相关地理信息。

检查无误后点击“保存”即可。
(4)预览图层
从左侧工具栏中进入“图层预览”页面,根据第(3)步中设置的图层名称找到新添加的图层,然后点击后面的“OpenLayers”就会打工一个新的页面预览选中的图层了,试着滚动一下鼠标滚轮,对图层进行放大缩小等操作。

通过以上4步操作,一个最简单的图层发布流程就演示完了,赶紧去试试吧!