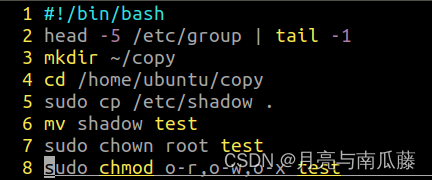
本文中,我将介绍半群,独异点,群,子群,阿贝尔群,陪集和拉格朗日定理
目录
半群,独异点,群的定义
子群判定定理
阿贝尔群
循环群
陪集与拉格朗日定理
半群,独异点,群的定义
在理解群之前,我们要先清楚什么是代数系统。其实代数系统可以简单理解成使用符号表示的某一种运算。其实和程序设计中算法的定义有点像,总的来说就可以把运算当成一个黑盒子,我们给定一个输入,那么就可以根据黑盒子的运算规则得到相应的输出。
我们举一个生活中的例子。有一台自动售货机,假设售货机只接收五元纸币和十元纸币,我们可以根据接收货币和吐出商品的情况给出这个代数系统的运算结果集,我们用*表示这个运算。
| 运算符号* | 五元纸币 | 十元纸币 |
| 五元纸币 | 橘子水 | 可乐 |
| 十元纸币 | 可乐 | 冰淇淋 |
上面的这个运算比较容易理解,就是你投入两张五元纸币,可以买到橘子水,投入一张十元纸币和一张五元纸币可以买到可乐,以此类推。
那么由于我们投入的是纸币,得到的是饮料或者食物,所以我们这个代数系统是不封闭的。
相对的,假如我们投入的是纸币,得到的也是纸币,那么我们就称这个代数系统是封闭的。
| △ | a | b |
| a | a | b |
| b | b | a |
上图的代数系统就是封闭的,下面我们来给出群的定义。
半群的定义:设<G, *>是一个代数系统,若*满足:
1)在G上的*运算是封闭的
2)G上的*运算是可结合的(如a*b*c=a*(b*c))
则<G, *>为半群。注意,这里的*不是单指乘法运算,而是广义的类似未知数的一个运算符代号,可以表示任意运算。
假设<G, *>是半群,并且:
3)G上的*运算存在幺元(或者说单位元)e
那么<G, *>是独异点。这里的幺元对于乘法运算来说就是1,对于加法运算来说就是0.
假设<G, *>是一个独异点,并且:
4)对于G中的每一个元素a,都存在元素b使得a*b=e
那么<G, *>是群,此时b为a的逆,a也为b的逆,可以记为b=a^(-1)
除了幺元之外,还有一个定义叫零元。在乘法中,幺元乘以任何一个数都是它本身,而零元乘以任何一个数都是零元。
例1: 设集合S={浅色,深色},定义在S上的二元运算*如下表所示
| * | 浅色 | 深色 |
| 浅色 | 浅色 | 浅色 |
| 深色 | 深色 | 深色 |
其中,浅色就是幺元,深色就是零元。
注:群中不可能有零元。
当代数系统<G, *>只满足*运算在G中封闭这个条件的时候,<G, *>是广群,我们用一张图描述各种群的包含关系。
设<G, *>是一个群,如果G是有限集,那么称<G, *>为有限群,G中元素的个数通常称为有限群的阶数,记为|G|;如果G是无限集,那么称<G, *>为无限群。
子群判定定理
子群判定定理1:设<G, *>是一个群,B是G的非空子集,如果B是一个有限集,那么,只要运算*在B上封闭,<B, *>必定是<G, *>的子群。
子群判定定理2:设<G, △>是群,S是G的非空子集,如果对于S的任意元素a,b有a△b^(-1)∈S,则<S, △>是<G, △>的子群。
阿贝尔群
如果群<G, *>中的*运算时可交换的,则称<G, *>为阿贝尔群,或称交换群
一个群<G, *>是阿贝尔群的充要条件是,对于任意a,b∈G,有(a*b)*(a*b)=(a*a)*(b*b)
循环群
设群<G, *>中存在一个元素a,是的G中所有的元素都是由a的幂构成的,则称群<G, *>为循环群,元素a称为群<G, *>的生成元
例如,60°就是群<{0°,60°,120°,180°,240°,360°},☆>的生成元,该群是一个循环群。
陪集与拉格朗日定理
陪集的定义:设<H, *>是<G, *>的子群,a∈G,则集合{a}H(H{a})称为由a确定的H在G中的左陪集(右陪集),简称为H关于a的左陪集(右陪集)
例如:设G=R*R,R为实数集,G上的一个二元运算+定义为
<x₁, y₁> + <x₂, y₂> = <x₁+x₂, y₁+y₂>
则,<G, +>是一个具有幺元<0, 0>的阿贝尔群
设H={<x, y>| y=2x},那么<H, +>是<G, +>的一个子群。对于<x0, y0>∈G, H关于<x0, y0>的左陪集为<x0, y0>H.
其中G为笛卡尔坐标系,H为y=2x的的直线,<x0, y0>H为与H平行的直线,因为我们可以找到一个实数b,使得y+y0=2(x+x0)+b
拉格朗日定理:设群<H, *>是群<G, *>的一个子群,则有:
a)R={<a, b>| a∈G, b∈G且a^(-1)*b∈H}是G的一个等价关系。对于a∈G,若记[a]R={x | x∈G且<a,x>∈R},则有[a]R=aH
b)如果G是有限群,|G|=n, |H|=m,则m|n(整除关系)
证明如下:
(a)对于任意a∈G,必有a^(-1)∈G,使得a*a^(-1)=e∈H,所以<a, a>∈R,满足自反性
若<a, b>∈R,则a^(-1)*b∈H,因为H是G的子群,所以有(a^(-1)*b)^(-1) = b^(-1)*a∈H,所以<b, a>∈R,满足对称性
若<a, b>∈R, <b, c>∈R,则有a^(-1)*b∈H并且b^(-1)*c∈H,由于运算的封闭性,有
a^(-1)*b*b^(-1)*c∈H,即a^(-1)*c∈H,即<a, c>∈H,满足传递性
综上所述,R是G上的一个等价关系,得证。 吧
对于a∈G,我们有:b∈[a]R,当且仅当<a, b>∈R,即当且仅当a^(-1)*b∈H,即b∈aH。因此[a]R=aH
(b)由于R是G中的一个等价关系,可以将G划分为等价类[a1]R,[a2]R,...[ak]R.
有G=∪[ai]R=∪aiH
对于H中任意两个不相等的h1和h2,a∈G,必有a*h1 ≠ a*h2,所以有|aiH|=|H|=m, i=1,2...k
所以n = |G| = (a1+a2+a3+...+ak)H = mk , 得证