AQS机制

1、什么是AQS？
AQS是抽象同步队列，基于CAS和LockSupport实现，通过资源状态state和AQS的同步队列实现线程抢占资源的管理。
2、获取资源
线程进来先获取资源，如果失败会重试一次，再次失败会将当前线程存放至同步队列，并调用park()阻塞当前线程。
3、释放资源
当线程释放资源的时候，会获取到同步队列中的头节点的next节点（因为头节点是当前线程），将next节点设置为头节点，并调用unpark()唤醒新头节点的线程去获取锁资源。
4、可重入锁
state的为2、3时，表示该资源被重入了。其原理为：当第一次获取资源失败，重试时会判断获取资源的线程是否为当前线程，如果是，则将state+1，返回ture。
5、为什么不唤醒所有阻塞的线程，而是只唤醒头节点的next节点？
　在链表中遍历唤醒所有线程效率低O(N)，而且根据链表中的存储顺序进行唤醒效率高O(1)，也比较公平。

6、为什么同步队列头节点为空节点？
头节点表示获取到锁的线程记录,为了GC回收方便,所以所有头节点都变为空。已经在aqs类中已经记录绑定获取到锁的线程，所以head结点直接设置为null，防止浪费空间内存。

一、Lock底层实现

　　Lock底层基于CAS+AQS组合实现。先CAS自旋，自旋失败使用AQS。
　　CAS：CPU底层实现，采用预值比较交换的机制。

二、使用LockSupport操作线程挂起与唤醒　　

　　LockSupport底层基于UnSafe类，调用c代码，将线程变为阻塞/唤醒。
　　线程挂起：AQS先通过CAS将没有获取到锁的线程添加到阻塞队列，再通过LockSupport.park()将线程变成阻塞，类似Synchronized锁对象的wait()方法。
　　线程唤醒：AQS先获取需要唤醒的线程节点（头节点的next节点），然后通过LockSupport.unpark(Thread thread)将线程唤醒。

三、AQS介绍

　　AQS(AbstractQueuedSynchronizer)：抽象同步队列类，底层基于CAS和LockSupport实现，通过资源变量State+AQS的同步管理队列（FIFO），实现了线程抢占资源的管理。
　　state：锁的状态；
　　ownerThread：持锁线程；
　　Node head,tail 双向链表头节点、尾节点 --prev、next、thread、awaitStatus；
　　park() 未获取到资源，将线程封装成node节点，存放在双向链表（同步队列）中，然后使用LockSupport.park()阻塞线程。awaitStatus = 0；
　　unpark() 线程释放资源，state = state-1。如果state=0，将ownerThread设为null，当前节点node设为头节点，node.prev = null，thread = null，awaitStatus = -1等；
　　await() 将当前线程存放至单向链表（阻塞队列），释放锁，使state设为0，使用LockSupport.park()将当前线程变为阻塞状态，awaitStatus = -2；
　　signal()：先采用CAS将线程线程状态awaitStatus由-2变为0，再将该线程追加到同步队列（双向链表）中。如果该线程获取到锁，修改节点状态awaitStatus=-1 。
　　AQS是一个抽象类，主要是通过继承的方式来使用，它本身没有实现任何的同步接口，仅仅是定义了同步状态的获取以及释放的方法来提供自定义的同步组件。

三、Lock锁的实现原理

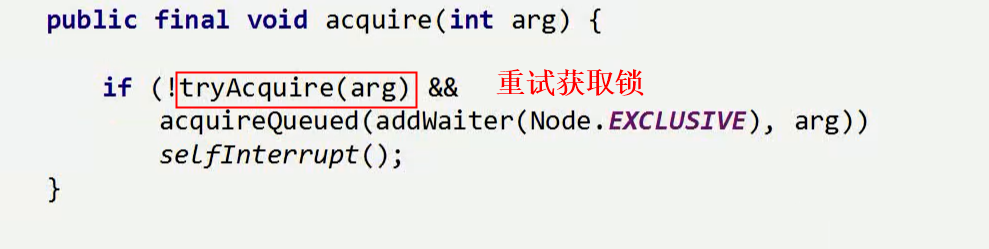
1）获取锁

2）重试获取锁&加入到阻塞队列

3）自旋重试或重入state+1

4）阻塞

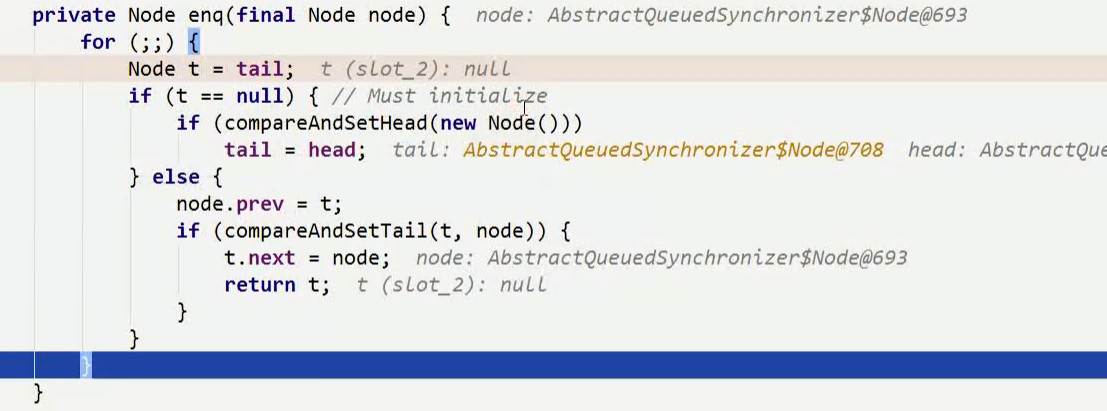
　　① 首先将未获取到锁的线程放入队列　　　

　　　　如果线程没有抢到锁，会放到阻塞链表的最后一个节点位置。该链表数据结构为FIFO队列，所以AQS队列遵循先进先出原则。
　　　　阻塞链表的头节点虽不为null，但为空值节点，不关联任何线程。

　　 ② 然后使用LockSupport.park()阻塞队列中的线程。

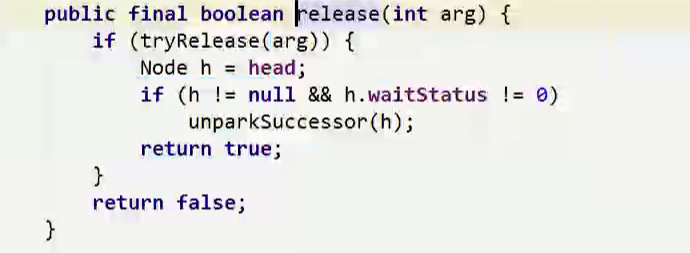
5）唤醒

　　为什么不唤醒所有阻塞的线程，而是只唤醒头节点的next节点？
　　答：在链表中遍历唤醒所有线程效率低O(N)，而且根据链表中的存储顺序进行唤醒效率高O(1)，也比较公平。

　　当唤醒的线程获取到锁，会将当前线程节点设置为head节点（thread=null，prev=null），即变为空节点，且设置原头节点.next=null，这样便于GC回收原头节点。

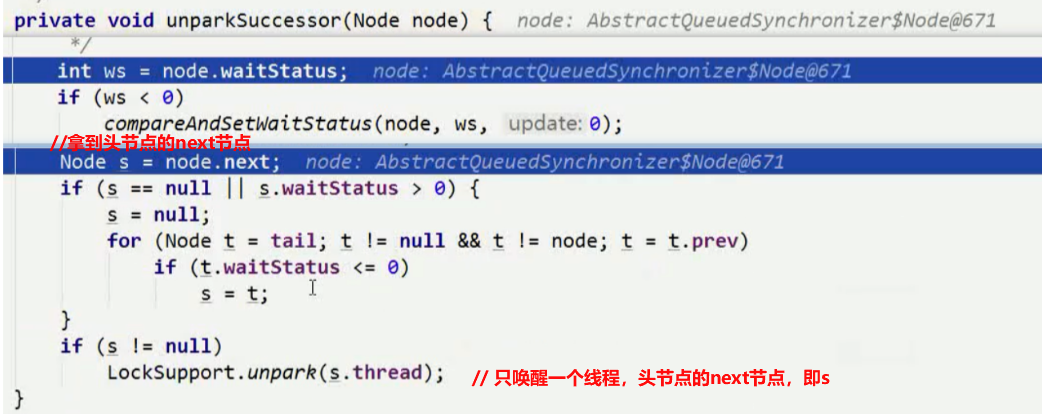
四、AQS底层如何实现公平与非公平锁

1、公平锁FairSync：严格遵守请求的

　　每一个线程获取锁的情况下，首先会判断，该线程是否为头节点的next节点，如果是，直接去获取锁；如果不是，则放入链表最后位置。
　　当持锁线程释放锁，会唤醒链表头节点的next节点，而不是唤醒所有线程，考虑因素（效率高、公平）。

2、非公平锁NonfairSync：通过竞争获取锁，效率高（唤醒锁的时候是公平的）

　　每一个线程获取锁的情况下，会进行一次重试，如果成功，即获取锁成功，执行代码；如果失败，则放入链表最后位置。
　　当持锁线程释放锁，会唤醒链表头节点的next节点，而不是唤醒所有线程，考虑因素（效率高、公平）。

　　非公平锁的效率更高，没有特殊要求的情况下使用非公平锁。
　　如：公平锁中，线程1释放锁后，需要唤醒其他线程获取锁，执行代码。如果线程1释放锁后，线程2进来，直接争抢锁，效率更高，毕竟唤醒锁的成本是比较高的。

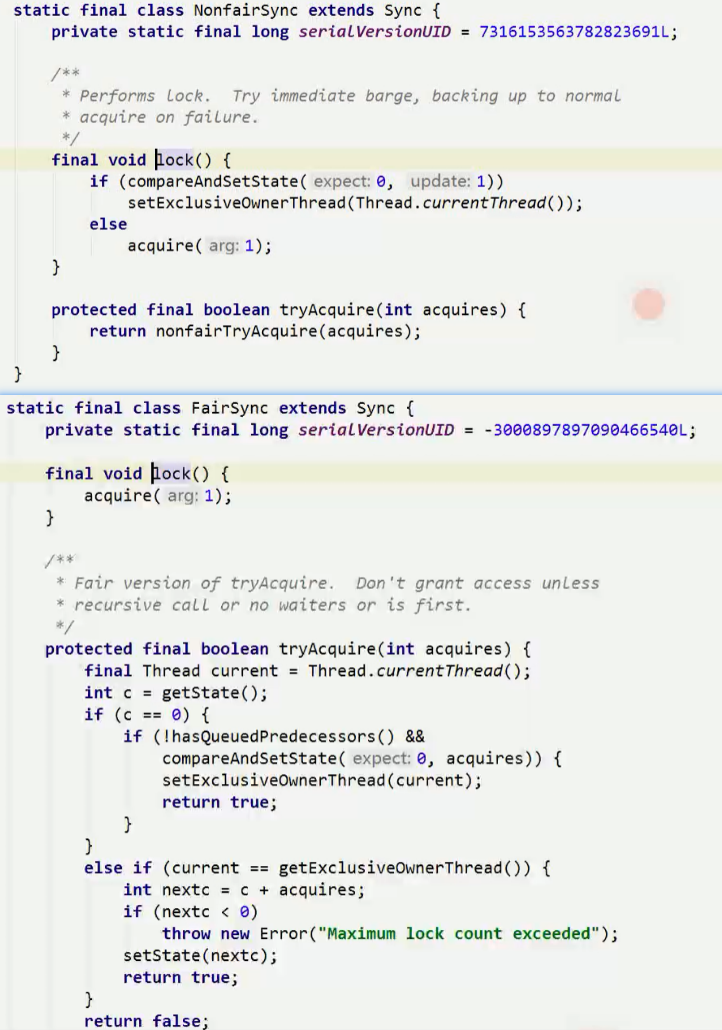
五、AQS如何唤醒正在等待的线程

　　当持锁线程释放锁，会唤醒链表头节点的next节点，而不是唤醒所有线程，考虑因素（效率高、公平）。

六、AbstractQueuedSynchronizer常用属性

1）Node head 头节点

2）Node tail 尾节点

3）Thread thread 记录没有抢到锁的线程（当前node封装的线程）

　　采用双向链表记录没有抢到锁的线程
　　在AQS中没有抢到锁的线程，放在链表中最后一个位置（头节点是空的，没有任何属性）

4）Int state 拿到锁的线程状态

　　0 没有任何线程获取到锁
　　1 已经有一个线程获取到锁
　　2、3... 说明该获取到线程可能重入了（Lock锁具有可重入性）。每调用lock锁的方法一次，state加1。调用unlock方法一次，state减1，完全释放锁的情况下state=0.

4）Int waitStatus 阻塞线程的状态

　　值为1，表示当前的线程被取消；
　　值为0，表示当前节点等待获取锁。
　　值为-1，表示等待持锁线程释放锁资源后唤醒当前节点；
　　值为-2，等待condition唤醒；
　　值为-3，工作于共享锁状态，需要向后传播，比如根据资源是否剩余，唤醒后继节点；

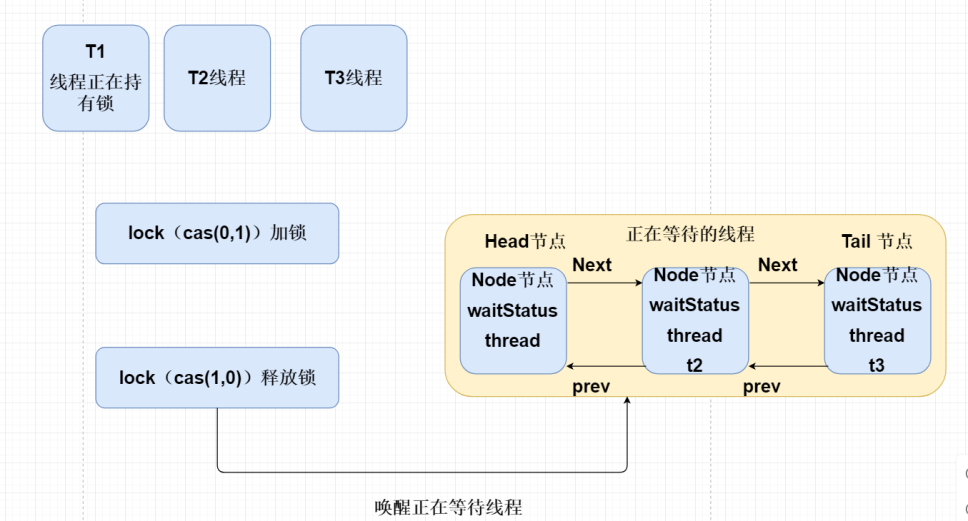
七、AQS中头节点为什么为空？

　　头节点表示获取到锁的线程记录,为了GC回收,所以所有头节点都变为空。
　　已经在aqs类中已经记录绑定获取到锁的线程，所以head结点直接设置为null，防止浪费空间内存。

八、AQS中的Condition源码解读

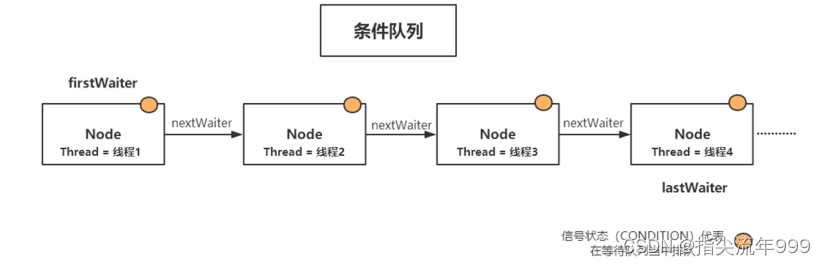
1、队列（链表）

　　等待队列：用于存放在lock锁中调用await方法,当前线程会变为阻塞状态，同时会释放锁单向链表存放
　　同步队列：用于存放没有竞争到锁，采用双向链表存放。

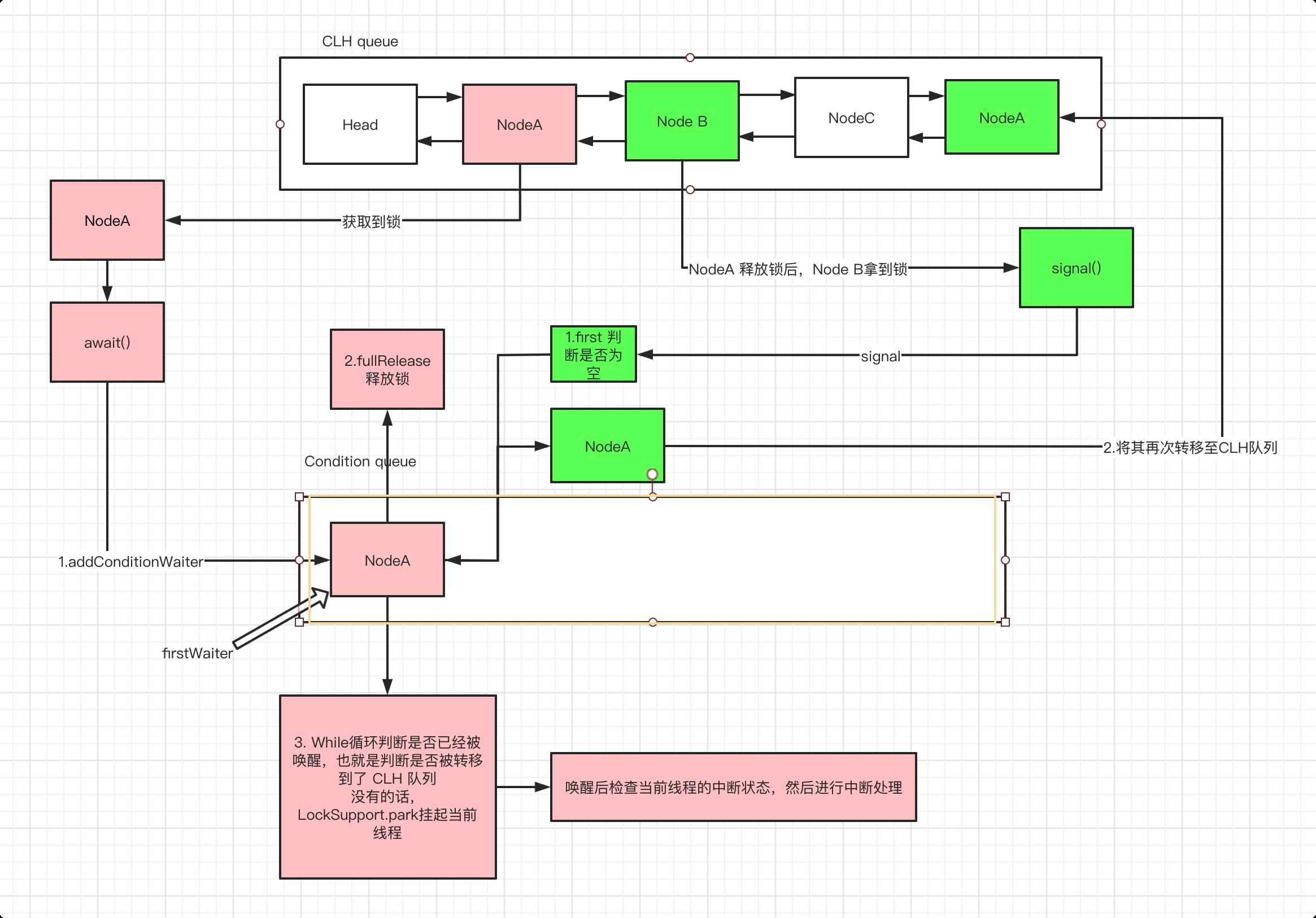
2、await方法阻塞

　　1）存放当前线程至condition单项链表
　　2）释放锁，使状态为0，唤醒其他线程获取锁。
　　3）将当前线程变为阻塞状态（waitStatus=-2）

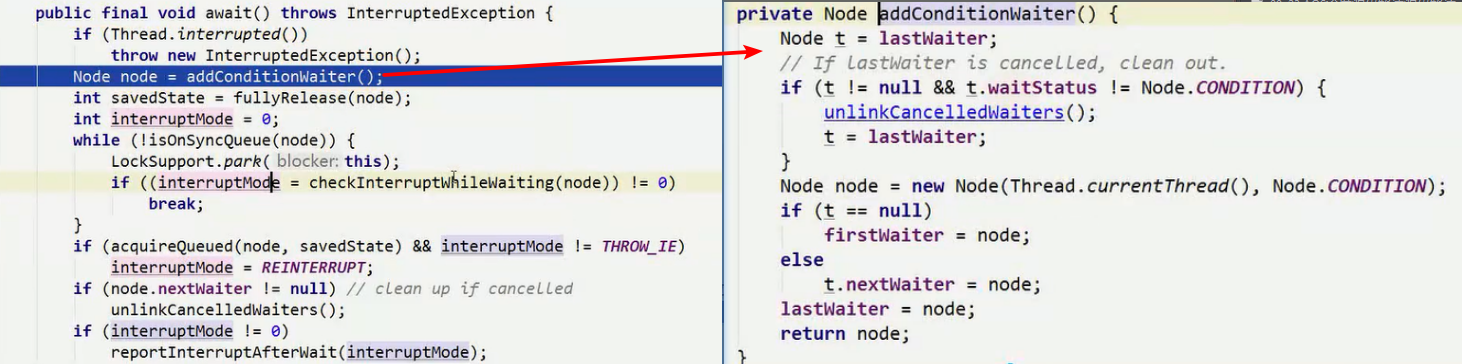
3、signal方法唤醒

　　condition.signal(); 只唤醒单项链表中第一个节点。
　　condition.signalAll(); 唤醒所有节点
　　　　获取到头节点，循环遍历并唤醒所有节点线程，去CAS参与锁的竞争，
　　1）采用CAS将线程线程状态由-2变为0
　　2）再将该线程追加到同步队列（双向链表）中，并修改状态为-1