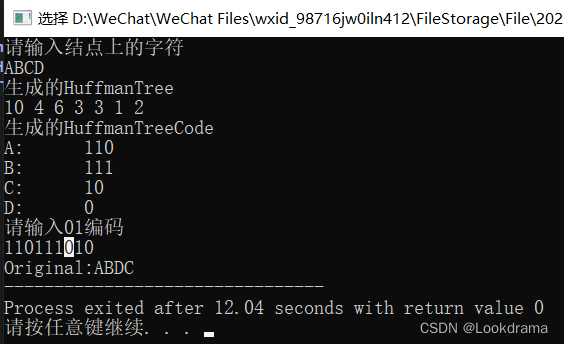
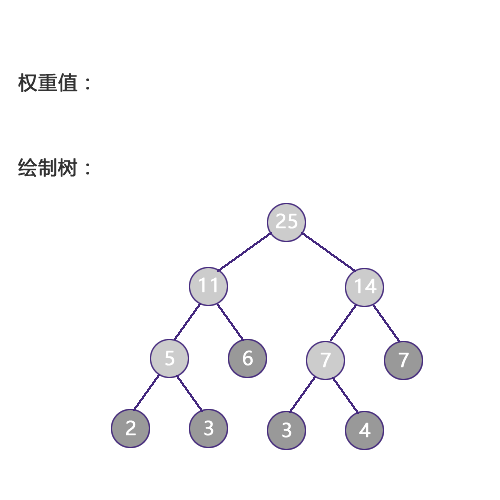
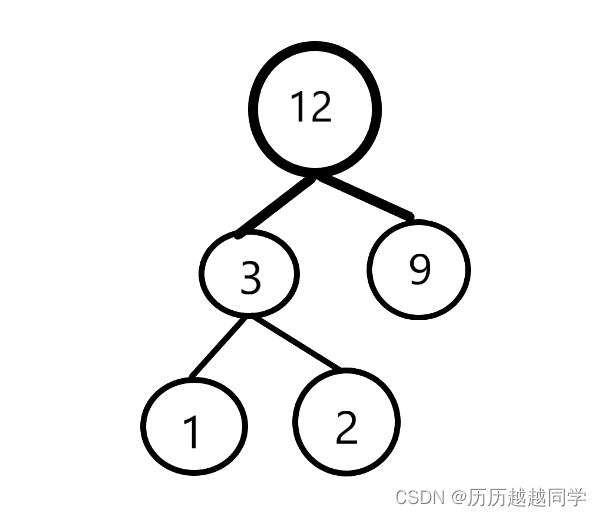
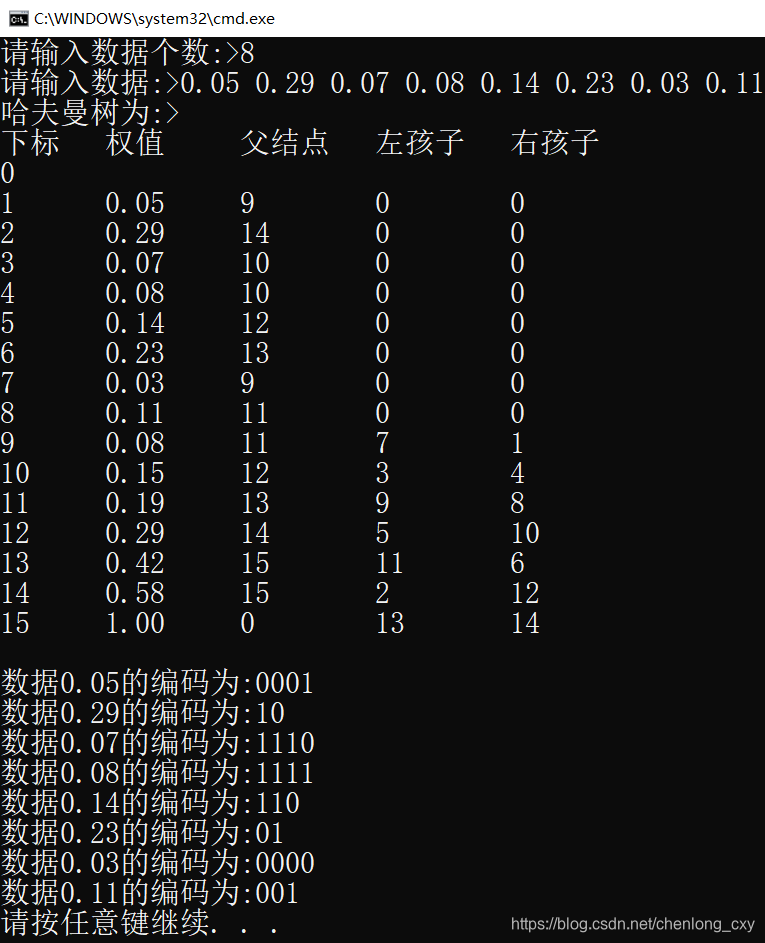
4-1 哈夫曼树 (100分)哈夫曼树
第一行输入一个数n,表示叶结点的个数。
需要用这些叶结点生成哈夫曼树,根据哈夫曼树的概念,这些结点有权值,即weight,题目需要输出哈夫曼树的带权路径长度(WPL)。
输入格式:
第一行输入一个数n,第二行输入n个叶结点(叶结点权值不超过1000,2<=n<=1000)。
输出格式:
在一行中输出WPL值。
输入样例:
5
1 2 2 5 9
输出样例:
37
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
#define OK 1
#define ERROR -1
#define OVERFLOW -2
typedef struct
{int weigth;int parent,Ichild,rchild;/* data */
}HTnode,*HuffmanTree;
void CreateHuffmantree(HuffmanTree &HT,int n);
int CountWeigth(HuffmanTree &HT,int n) ;
int Count(HuffmanTree &HT,int i) ;//求各个叶子的路径长,递归算法,
int main()
{int n;//n为叶子节点个数cin>>n;if(n<2||n>1000)return 0;HuffmanTree HT;CreateHuffmantree(HT,n);cout<<CountWeigth(HT,n);system("pause");return 0;
}
int CountWeigth(HuffmanTree &HT,int n)
{int wpl=0;for(int i=1;i<=n;i++){wpl=HT[i].weigth*Count(HT,i)+wpl;}return wpl;
}
int Count(HuffmanTree &HT,int i) //求各个叶子的路径长,递归算法,
{int j;if(HT[i].parent==0)return 0;else{j=HT[i].parent; //回溯到双亲节点下标return 1+Count(HT,j);/* code */}
}
void Select(HuffmanTree &HT,int len,int &s1,int &s2) //从形式上看,s1和s2用地址比较好,选最小,查找操作,不改变原值
{
int i,max=1000,temp,min;//j记录下标
int k=1;
while(HT[k].parent!=0)
{k++;
} //找双亲不为0的节点作为假设
for(i=2;i<=len;i++) //例如当第一次循环,前n个节点,叶子权值已知,选择最小的两个
{if(HT[i].weigth<HT[k].weigth &&HT[i].parent==0)k=i;
}
s1=k;
temp=HT[s1].weigth;HT[s1].weigth=max;//s1为最小,接下的s2的值>=s1,s1定义为一个大的数值,就不会被选中
k=1;
while(HT[k].parent!=0)
{k++;
} //找双亲不为0的节点作为假设
for(i=2;i<=len;i++) //例如当第一次循环,前n个节点,叶子权值已知,选择最小的两个
{if(HT[i].weigth<HT[k].weigth &&HT[i].parent==0)k=i;
}
s2=k;
HT[s1].weigth=temp;//将s1的原值还给s1
}
void CreateHuffmantree(HuffmanTree &HT,int n)
{if (n<1) //只有一个节点时,没有意义{return ;//函数结束}int m=n*2-1;//m为节点总数,根据哈夫曼数性质HT=new HTnode[m+1];//不要0号元素,1开始, n个节点,n-1次循环,所以总共m次,因为不用0号,所以需要m+1个;for (int i = 1; i <=m; i++){HT[i].Ichild=0;/* code */HT[i].parent=0;HT[i].rchild=0; //初始化哈夫曼表}for(int j=1;j<=n;j++)//赋予叶子节点权值 //前n个,不是后面n-1个;n-1个自动求{cin>>HT[j].weigth;}int s1=0,s2=0;for(int k=n+1;k<=m;k++)//求n之后,即是n-1轮的weigth值,即向下求数{Select(HT,k-1,s1,s2); //s1和s2都是下标,是i-1之前的已经求出和已经定义的得到的HT[s1].parent=k;HT[s2].parent=k; //合并,s1和s2的parent为iHT[k].Ichild=s1;HT[k].rchild=s2;//将i的左右孩子设置为s1,s2HT[k].weigth=HT[s1].weigth+HT[s2].weigth; //得到i的权值,通过左右孩子 }}运行结果