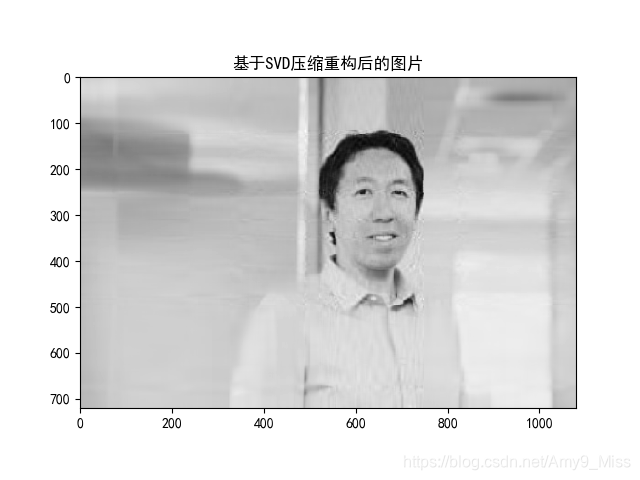
SVD奇异值分解
- 前言
- 理论推导
- 部分代码实现
前言
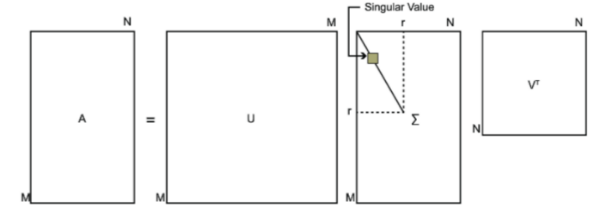
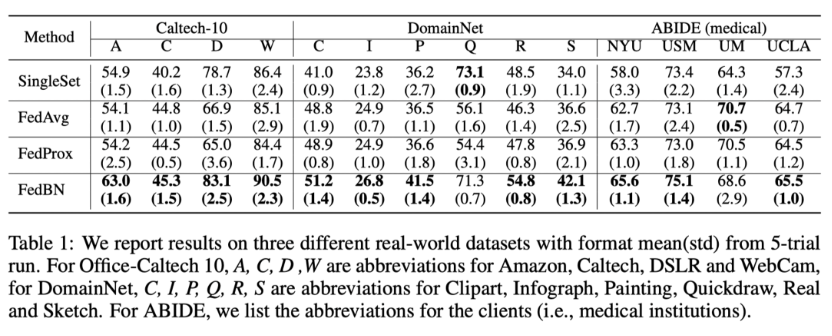
奇异值分解(singular value decomposition,以下简称SVD)是线性代数中一种重要的矩阵分解。SVD将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。SVD将矩阵 A A A分解成三个矩阵的乘积
A = U D V T A = UDV^{T} A=UDVT
设 A A A是 m × n m\times n m×n的矩阵,则 U U U是一个 m × m m\times m m×m的矩阵, D D D是一个 m × n m\times n m×n的矩阵 V V V是一个 n × n n\times n n×n的矩阵。
读者可访问以下链接获取相关代码
代码链接
理论推导

部分代码实现
/*** @brief 实现奇异值分解* @note 基于Householder变换以及变星QR算法对一般实矩阵A进行奇异值分解* step1 用豪斯荷尔德变换将A约化为双对角线矩阵* step2 用变星的QR算法进行迭代,计算所有奇异值* steo3 对奇异值按非递增次序进行排列
*/
void Matrix::SVD( const Matrix & A, Matrix& U2, Matrix& W, Matrix& V) {Matrix U = A;int m = A.rows();int n = A.cols();U2 = Matrix(m, m);V = Matrix(n, n);NAFLOAT* w = (NAFLOAT*)malloc(n * sizeof(NAFLOAT));NAFLOAT* rv1 = (NAFLOAT*)malloc(n * sizeof(NAFLOAT));int32_t flag, i, its, j, jj, k, l, nm;NAFLOAT anorm, c, f, g, h, s, scale, x, y, z;g = scale = anorm = 0.0;for (i = 0; i < n; i++) {l = i + 1;rv1[i] = scale * g;g = s = scale = 0.0;if (i < m) {for (k = i; k < m; k++) scale += fabs(U.m_val[k][i]);if (scale) {for (k = i; k < m; k++) {U.m_val[k][i] /= scale;s += U.m_val[k][i] * U.m_val[k][i];}f = U.m_val[i][i];g = -SIGN(sqrt(s), f);h = f * g - s;U.m_val[i][i] = f - g;for (j = l; j < n; j++) {for (s = 0.0, k = i; k < m; k++) s += U.m_val[k][i] * U.m_val[k][j];f = s / h;for (k = i; k < m; k++) U.m_val[k][j] += f * U.m_val[k][i];}for (k = i; k < m; k++) U.m_val[k][i] *= scale;}}w[i] = scale * g;g = s = scale = 0.0;if (i < m && i != n - 1) {for (k = l; k < n; k++) scale += fabs(U.m_val[i][k]);if (scale) {for (k = l; k < n; k++) {U.m_val[i][k] /= scale;s += U.m_val[i][k] * U.m_val[i][k];}f = U.m_val[i][l];g = -SIGN(sqrt(s), f);h = f * g - s;U.m_val[i][l] = f - g;for (k = l; k < n; k++) rv1[k] = U.m_val[i][k] / h;for (j = l; j < m; j++) {for (s = 0.0, k = l; k < n; k++) s += U.m_val[j][k] * U.m_val[i][k];for (k = l; k < n; k++) U.m_val[j][k] += s * rv1[k];}for (k = l; k < n; k++) U.m_val[i][k] *= scale;}}anorm = std::max(anorm, (std::fabs(w[i]) + std::fabs(rv1[i])));}for (i = n - 1; i >= 0; i--) { // Accumulation of right-hand transformations.if (i < n - 1) {if (g) {for (j = l; j < n; j++) // Double division to avoid possible underflow.V.m_val[j][i] = (U.m_val[i][j] / U.m_val[i][l]) / g;for (j = l; j < n; j++) {for (s = 0.0, k = l; k < n; k++) s += U.m_val[i][k] * V.m_val[k][j];for (k = l; k < n; k++) V.m_val[k][j] += s * V.m_val[k][i];}}for (j = l; j < n; j++) V.m_val[i][j] = V.m_val[j][i] = 0.0;}V.m_val[i][i] = 1.0;g = rv1[i];l = i;}for (i = std::min(m, n) - 1; i >= 0; --i) { // Accumulation of left-hand transformations.l = i + 1;g = w[i];for (j = l; j < n; j++) U.m_val[i][j] = 0.0;if (g) {g = 1.0 / g;for (j = l; j < n; j++) {for (s = 0.0, k = l; k < m; k++) s += U.m_val[k][i] * U.m_val[k][j];f = (s / U.m_val[i][i]) * g;for (k = i; k < m; k++) U.m_val[k][j] += f * U.m_val[k][i];}for (j = i; j < m; j++) U.m_val[j][i] *= g;}else for (j = i; j < m; j++) U.m_val[j][i] = 0.0;++U.m_val[i][i];}for (k = n - 1; k >= 0; k--) { // Diagonalization of the bidiagonal form: Loop over singular values,for (its = 0; its < 30; its++) { // and over allowed iterations.flag = 1;for (l = k; l >= 0; l--) { // Test for splitting.nm = l - 1;if ((NAFLOAT)(fabs(rv1[l]) + anorm) == anorm) { flag = 0; break; }if ((NAFLOAT)(fabs(w[nm]) + anorm) == anorm) { break; }}if (flag) {c = 0.0; // Cancellation of rv1[l], if l > 1.s = 1.0;for (i = l; i <= k; i++) {f = s * rv1[i];rv1[i] = c * rv1[i];if ((NAFLOAT)(fabs(f) + anorm) == anorm) break;g = w[i];h = pythag(f, g);w[i] = h;h = 1.0 / h;c = g * h;s = -f * h;for (j = 0; j < m; j++) {y = U.m_val[j][nm];z = U.m_val[j][i];U.m_val[j][nm] = y * c + z * s;U.m_val[j][i] = z * c - y * s;}}}z = w[k];if (l == k) { // Convergence.if (z < 0.0) { // Singular value is made nonnegative.w[k] = -z;for (j = 0; j < n; j++) V.m_val[j][k] = -V.m_val[j][k];}break;}NA_Assert(its != 29,"ERROR in SVD: No convergence in 30 iterations");x = w[l]; // Shift from bottom 2-by-2 minor.nm = k - 1;y = w[nm];g = rv1[nm];h = rv1[k];f = ((y - z) * (y + z) + (g - h) * (g + h)) / (2.0 * h * y);g = pythag(f, 1.0);f = ((x - z) * (x + z) + h * ((y / (f + SIGN(g, f))) - h)) / x;c = s = 1.0; // Next QR transformation:for (j = l; j <= nm; j++) {i = j + 1;g = rv1[i];y = w[i];h = s * g;g = c * g;z = pythag(f, h);rv1[j] = z;c = f / z;s = h / z;f = x * c + g * s;g = g * c - x * s;h = y * s;y *= c;for (jj = 0; jj < n; jj++) {x = V.m_val[jj][j];z = V.m_val[jj][i];V.m_val[jj][j] = x * c + z * s;V.m_val[jj][i] = z * c - x * s;}z = pythag(f, h);w[j] = z; // Rotation can be arbitrary if z = 0.if (z) {z = 1.0 / z;c = f * z;s = h * z;}f = c * g + s * y;x = c * y - s * g;for (jj = 0; jj < m; jj++) {y = U.m_val[jj][j];z = U.m_val[jj][i];U.m_val[jj][j] = y * c + z * s;U.m_val[jj][i] = z * c - y * s;}}rv1[l] = 0.0;rv1[k] = f;w[k] = x;}}// sort singular values and corresponding columns of u and v// by decreasing magnitude. Also, signs of corresponding columns are// flipped so as to maximize the number of positive elements.int32_t s2, inc = 1;NAFLOAT sw;NAFLOAT* su = (NAFLOAT*)malloc(m * sizeof(NAFLOAT));NAFLOAT* sv = (NAFLOAT*)malloc(n * sizeof(NAFLOAT));do { inc *= 3; inc++; } while (inc <= n);do {inc /= 3;for (i = inc; i < n; i++) {sw = w[i];for (k = 0; k < m; k++) su[k] = U.m_val[k][i];for (k = 0; k < n; k++) sv[k] = V.m_val[k][i];j = i;while (w[j - inc] < sw) {w[j] = w[j - inc];for (k = 0; k < m; k++) U.m_val[k][j] = U.m_val[k][j - inc];for (k = 0; k < n; k++) V.m_val[k][j] = V.m_val[k][j - inc];j -= inc;if (j < inc) break;}w[j] = sw;for (k = 0; k < m; k++) U.m_val[k][j] = su[k];for (k = 0; k < n; k++) V.m_val[k][j] = sv[k];}} while (inc > 1);for (k = 0; k < n; k++) { // flip signss2 = 0;for (i = 0; i < m; i++) if (U.m_val[i][k] < 0.0) s2++;for (j = 0; j < n; j++) if (V.m_val[j][k] < 0.0) s2++;if (s2 > (m + n) / 2) {for (i = 0; i < m; i++) U.m_val[i][k] = -U.m_val[i][k];for (j = 0; j < n; j++) V.m_val[j][k] = -V.m_val[j][k];}}// create vector and copy singular valuesW = Matrix(std::min(m, n), 1, w);// extract mxm submatrix UU2.setMat(U.getMat(0, 0, m - 1, std::min(m - 1, n - 1)), 0, 0);// release temporary memoryfree(w);free(rv1);free(su);free(sv);
}