奇异值分解
- 1.奇异值分解
- 1.1 变换(Transformations)
- 1.2 线性变换(Linear Transformations)
- 1.3 降维(Dimensionality Reduction)
- 1.4 奇异值分解(SVD)
- 1.5 图像压缩(Image Compression)
- 1.6 如何计算分解的三个矩阵?
- 1.7 联系与区别
- 1.7.1 特征值和特征向量
- 1.7.2 奇异值和奇异向量
- 1.8 矩阵估计(Matrix Approximation with SVD)
1.奇异值分解
笔记来源:Singular Value Decomposition (SVD) and Image Compression
1.1 变换(Transformations)
左侧图形先进行水平方向缩放,再进行垂直方向缩放,而后进行旋转,发现经过一系列变换后与右侧图形不符,说明缩放和旋转的操作有时是有顺序的

正确操作:先进行旋转,再进行水平方向缩放,而后进行垂直方向缩放,得到与右侧一致的图形

1.2 线性变换(Linear Transformations)




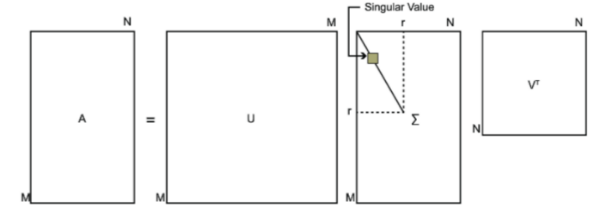
一步复杂变换 A A A(主要考虑高维)分解为了三个简单变换 V † 、 Σ 、 U V^{\dagger}、\Sigma、U V†、Σ、U

1.3 降维(Dimensionality Reduction)
我们将上述矩阵 Σ \Sigma Σ中的 σ 2 = 0.44 \sigma_2=0.44 σ2=0.44 修改为 σ 2 = 0 \sigma_2=0 σ2=0 ,二维图形直接被压缩成了一维

降维的好处:存储数据减少


1.4 奇异值分解(SVD)
1.4.1 如果矩阵 A A A是方阵(Square Matrix)


例子:

1.4.2 如果矩阵 A A A是非方阵(Non-Square Matrix)

1.5 图像压缩(Image Compression)

1.6 如何计算分解的三个矩阵?

U = [ u 1 u 2 ⋯ ] Σ = d i a g [ σ 1 σ 2 ⋯ ] V T = [ v 1 T v 2 T ⋮ ] U=\begin{bmatrix}\boldsymbol{u}_1 & \boldsymbol{u}_2 & \cdots \end{bmatrix}\\ ~\\ \Sigma=diag\begin{bmatrix}\sigma_1 & \sigma_2 & \cdots \end{bmatrix}\\ ~\\ V^{T}=\begin{bmatrix}v_1^T \\ v_2^T\\ \vdots\end{bmatrix} U=[u1u2⋯] Σ=diag[σ1σ2⋯] VT=⎣⎢⎡v1Tv2T⋮⎦⎥⎤

计算矩阵 A A A的特征值
d e t A = λ 1 λ 2 = 15 t r A = λ 1 + λ 2 = 8 λ 1 = 3 、 λ 2 = 5 det\ A=\lambda_1\lambda_2=15\\ ~\\ tr\ A=\lambda_1+\lambda_2=8\\ ~\\ \lambda_1=3、\lambda_2=5 det A=λ1λ2=15 tr A=λ1+λ2=8 λ1=3、λ2=5
计算 A A T AA^T AAT
A A T u i = σ i 2 u i A A T = [ 3 0 4 5 ] [ 3 4 0 5 ] = [ 25 20 20 25 ] AA^T\boldsymbol{u}_i=\sigma^2_i\boldsymbol{u}_i\\ ~\\ AA^T= \begin{bmatrix}3 & 0\\ 4 & 5\end{bmatrix} \begin{bmatrix}3 & 4\\ 0 & 5\end{bmatrix}= \begin{bmatrix}25 & 20\\ 20 & 25\end{bmatrix} AATui=σi2ui AAT=[3405][3045]=[25202025]
计算 A A T AA^T AAT的特征值 σ 2 \sigma^2 σ2【这里的 σ \sigma σ 叫做矩阵 A A A的奇异值】
法一: d e t ( A A T − σ I ) = 0 det(AA^T-\sigma I)=0 det(AAT−σI)=0
法二:
d e t A A T = 225 = σ 1 2 σ 2 2 t r A A T = 50 = σ 1 2 + σ 2 2 σ 1 2 = 45 、 σ 2 2 = 5 σ 1 = 45 、 σ 2 = 5 σ 1 σ 2 = 15 = d e t A det\ AA^T=225=\sigma_1^2\sigma_2^2\\ tr\ AA^T=50=\sigma_1^2+\sigma_2^2\\ \sigma_1^2=45、\sigma_2^2=5\\ \sigma_1=\sqrt{45}、\sigma_2=\sqrt{5}\\ \sigma_1\sigma_2=15=det\ A det AAT=225=σ12σ22tr AAT=50=σ12+σ22σ12=45、σ22=5σ1=45、σ2=5σ1σ2=15=det A
计算 A T A A^TA ATA
A T A v i = σ i 2 v i A T A = [ 3 4 0 5 ] [ 3 0 4 5 ] = [ 9 12 12 41 ] A^TA\boldsymbol{v}_i=\sigma^2_i\boldsymbol{v}_i\\ ~\\ A^TA=\begin{bmatrix}3 & 4\\ 0 & 5\end{bmatrix} \begin{bmatrix}3 & 0\\ 4 & 5\end{bmatrix}= \begin{bmatrix}9 & 12\\ 12 & 41\end{bmatrix} ATAvi=σi2vi ATA=[3045][3405]=[9121241]
计算 A T A A^TA ATA的特征向量 v 1 \boldsymbol{v}_1 v1【这里的 v 1 \boldsymbol{v}_1 v1 是矩阵 A A A 的右奇异向量】
A T A v 1 = σ 1 2 v 1 [ 9 12 12 41 ] [ a 1 a 2 ] = 45 [ a 1 a 2 ] a 1 = a 2 [ 9 12 12 41 ] [ 1 1 ] = 45 [ 1 1 ] A^TA\boldsymbol{v}_1=\sigma_1^2\boldsymbol{v}_1\\ ~\\ \begin{bmatrix}9 & 12\\ 12 & 41\end{bmatrix} \begin{bmatrix}a_1 \\ a_2\end{bmatrix}=45 \begin{bmatrix}a_1 \\ a_2\end{bmatrix}\\ ~\\ a_1=a_2\\ ~\\ \begin{bmatrix}9 & 12\\ 12 & 41\end{bmatrix} \begin{bmatrix}1 \\ 1\end{bmatrix}=45 \begin{bmatrix}1 \\ 1\end{bmatrix} ATAv1=σ12v1 [9121241][a1a2]=45[a1a2] a1=a2 [9121241][11]=45[11]
计算 A T A A^TA ATA的特征向量 v 2 \boldsymbol{v}_2 v2【这里的 v 2 \boldsymbol{v}_2 v2 是矩阵 A A A 的右奇异向量】
A T A v 2 = σ 2 2 v 2 [ 9 12 12 41 ] [ a 3 a 4 ] = 5 [ a 3 a 4 ] a 3 = − a 4 [ 9 12 12 41 ] [ − 1 1 ] = 5 [ − 1 1 ] A^TA\boldsymbol{v}_2=\sigma_2^2\boldsymbol{v}_2\\ ~\\ \begin{bmatrix}9 & 12\\ 12 & 41\end{bmatrix} \begin{bmatrix}a_3 \\ a_4\end{bmatrix}=5 \begin{bmatrix}a_3 \\ a_4\end{bmatrix}\\ ~\\ a_3=-a_4\\ ~\\ \begin{bmatrix}9 & 12\\ 12 & 41\end{bmatrix} \begin{bmatrix}-1 \\ 1\end{bmatrix}=5 \begin{bmatrix}-1 \\ 1\end{bmatrix} ATAv2=σ22v2 [9121241][a3a4]=5[a3a4] a3=−a4 [9121241][−11]=5[−11]
单位化后的矩阵 A A A的右奇异向量 v 1 、 v 2 \boldsymbol{v}_1、\boldsymbol{v}_2 v1、v2
v 1 = 1 2 [ 1 1 ] 、 v 2 = 1 2 [ − 1 1 ] \boldsymbol{v}_1=\frac{1}{\sqrt{2}}\begin{bmatrix}1 \\ 1\end{bmatrix}、\boldsymbol{v}_2=\frac{1}{\sqrt{2}}\begin{bmatrix}-1 \\ 1\end{bmatrix} v1=21[11]、v2=21[−11]
计算矩阵 A A A的左奇异向量 u 1 、 u 2 \boldsymbol{u}_1、\boldsymbol{u}_2 u1、u2
A v 1 = σ 1 u 1 u 1 = A v 1 σ 1 = [ 1 3 ] A v 2 = σ 2 u 2 u 2 = A v 2 σ 2 = [ − 3 1 ] A\boldsymbol{v}_1=\sigma_1\boldsymbol{u}_1\\ ~\\ \boldsymbol{u}_1=\frac{A\boldsymbol{v}_1}{\sigma_1}=\begin{bmatrix}1 \\ 3\end{bmatrix}\\ ~\\ A\boldsymbol{v}_2=\sigma_2\boldsymbol{u}_2\\ ~\\ \boldsymbol{u}_2=\frac{A\boldsymbol{v}_2}{\sigma_2}=\begin{bmatrix}-3 \\ 1\end{bmatrix} Av1=σ1u1 u1=σ1Av1=[13] Av2=σ2u2 u2=σ2Av2=[−31]
单位化矩阵 A A A的左奇异向量 u 1 、 u 2 \boldsymbol{u}_1、\boldsymbol{u}_2 u1、u2
u 1 = 1 10 [ 1 3 ] 、 u 2 = 1 10 [ − 3 1 ] \boldsymbol{u}_1=\frac{1}{\sqrt{10}}\begin{bmatrix}1 \\ 3\end{bmatrix}、\boldsymbol{u}_2=\frac{1}{\sqrt{10}}\begin{bmatrix}-3 \\ 1\end{bmatrix} u1=101[13]、u2=101[−31]
分解成的三个矩阵


1.7 联系与区别
笔记来源:Understanding Eigenvalues and Singular Values
联系:特征值和奇异值都描述了线性变换的量级或者说是变换幅度
They (eigenvalues and singular values) both describe the behavior of a matrix on a certain set of vectors.
And the corresponding eigen- and singular values describe the magnitude of that action.
1.7.1 特征值和特征向量
本人相关博客:特征值、特征向量、迹
笔记来源:Understanding Eigenvalues and Singular Values
The eigenvectors of a matrix describe the directions of its invariant action.(不变作用方向)
That eigenvectors give the directions of invariant action is obvious from the definition. The definition says that when A acts on an eigenvector, it just multiplies it by a constant, the corresponding eigenvalue. In other words, when a linear transformation acts on one of its eigenvectors, it shrinks the vector or stretches it and reverses its direction if λ is negative, but never changes the direction otherwise. The action is invariant.
A v = λ v A\boldsymbol{v}=\lambda\boldsymbol{v} Av=λv
the vector v \boldsymbol{v} v is called eigenvector
A scalar λ \lambda λ is called eigenvalue of A A A


1.7.2 奇异值和奇异向量
笔记来源:Understanding Eigenvalues and Singular Values
A v = σ u A ∗ u = σ v A\boldsymbol{v}=\sigma\boldsymbol{u}\\ A^*\boldsymbol{u}=\sigma\boldsymbol{v} Av=σuA∗u=σv
where A ∗ A^* A∗ is the conjugate transpose of A A A



A v 1 = σ 1 u 1 A v 2 = σ 2 u 2 A\boldsymbol{v}_1=\sigma_1\boldsymbol{u}_1\\ A\boldsymbol{v}_2=\sigma_2\boldsymbol{u}_2 Av1=σ1u1Av2=σ2u2
A scalar σ \sigma σ is a singular value of A A A
σ 1 \sigma_1 σ1 is the largest singular value of A A A with right singular vector v \boldsymbol{v} v
σ 2 \sigma_2 σ2 is the least singular value of A A A with left singular vector u \boldsymbol{u} u
the vectors u 、 v \boldsymbol{u}、\boldsymbol{v} u、v are singular vectors
the vector u \boldsymbol{u} u is called a left singular vectors
the vector v \boldsymbol{v} v is called a right singular vectors
The singular vectors of a matrix describe the directions of its maximum action. (最大作用方向)
矩阵 A A A对原空间中的任一单位向量 x \boldsymbol{x} x进行变换
arg max x , ∣ ∣ x ∣ ∣ = 1 ∣ ∣ A x ∣ ∣ = ∣ ∣ A v ∣ ∣ = σ 1 \argmax\limits_{\boldsymbol{x},||\boldsymbol{x}||=1}||A\boldsymbol{x}||=||A\boldsymbol{v}||=\sigma_1 x,∣∣x∣∣=1argmax∣∣Ax∣∣=∣∣Av∣∣=σ1
所有单位向量 x \boldsymbol{x} x中某一个向量长度变换最大,它就是右奇异向量 v \boldsymbol{v} v
其在矩阵 A A A的作用下,长度 ∣ ∣ A v ∣ ∣ = σ 1 ||A\boldsymbol{v}||=\sigma_1 ∣∣Av∣∣=σ1
单位圆经过线性变换 A A A得到椭圆
右奇异向量 v \boldsymbol{v} v在椭圆的半长轴上
左奇异向量 u \boldsymbol{u} u在椭圆的半短轴上
拓展到三维空间



1.8 矩阵估计(Matrix Approximation with SVD)

将当前最大奇异值 3 3 3 改写为 0 0 0

改写后矩阵 A 1 A_1 A1 对应的线性变换如下图

将矩阵 A 1 A_1 A1中的当前最大奇异值 2 2 2 改写为 0 0 0

改写后矩阵 A 2 A_2 A2 对应的线性变换如下图


重点:每一个奇异向量都会产生一个线性子空间中的标准正交基
在所有方向正交于有最大奇异向量(最大奇异值对应的向量)中,一个奇异值和其奇异向量将给出最大作用的方向
重要应用:
1.在一些统计学、机器学习中要求找到某个矩阵的低秩估计(Low-rank approximation)
2.主成分分析(PCA)也是这一类问题,即用一些最大方差的不相关分量近似某个观测矩阵X
具体做法:
计算SVD并将最小的奇异值改为0