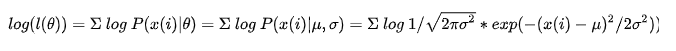转载来源:
作者:Xinyu Chen
链接:https://zhuanlan.zhihu.com/p/26306568
来源:知乎
矩阵的奇异值分解(singular value decomposition,简称SVD)是线性代数中很重要的内容,并且奇异值分解过程也是线性代数中相似对角化分解(也被称为特征值分解,eigenvalue decomposition,简称EVD)的延伸。因此,以下将从线性代数中最基础的矩阵分解开始讲起,引出奇异值分解的定义,并最终给出奇异值分解的低秩逼近问题相关的证明过程。
1 线性代数中的矩阵分解
我们在学习线性代数时,就已经接触了线性代数中的两个重要定理,即对角化定理和相似对角化定理,在这里,我们先简单地回顾一下这两个定理。另外,在接下来的篇幅里,我们所提到的矩阵都是指由实数构成的矩阵,即实矩阵。
给定一个大小为的矩阵
(是方阵),其对角化分解可以写成
其中,的每一列都是特征向量,
对角线上的元素是从大到小排列的特征值,若将
记作
,则
更为特殊的是,当矩阵是一个对称矩阵时,则存在一个对称对角化分解,即
其中,的每一列都是相互正交的特征向量,且是单位向量,
对角线上的元素是从大到小排列的特征值。
当然,将矩阵记作
,则矩阵
也可以写成如下形式:
举一个简单的例子,如给定一个大小为的矩阵
,根据
求得特征值为
,
,相应地,
,
,则
.
这样,我们就很容易地得到了矩阵的对称对角化分解。
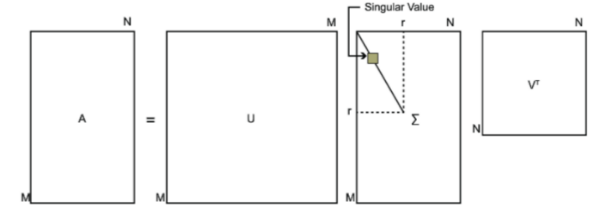
2 奇异值分解的定义
在上面,对于对称的方阵而言,我们能够进行对称对角化分解,试想:对称对角化分解与奇异值分解有什么本质关系呢?
当给定一个大小为的矩阵
,虽然矩阵
不一定是方阵,但大小为
的
和
的
却是对称矩阵,若
,
,则矩阵
的奇异值分解为
其中,矩阵的大小为
,列向量
是
的特征向量,也被称为矩阵
的左奇异向量(left singular vector);矩阵
的大小为
,列向量
是
的特征向量,也被称为矩阵
的右奇异向量(right singular vector);矩阵
大小为
,矩阵
大小为
,两个矩阵对角线上的非零元素相同(即矩阵
和矩阵
的非零特征值相同,推导过程见附录1);矩阵
的大小为
,位于对角线上的元素被称为奇异值(singular value)。
接下来,我们来看看矩阵与矩阵
和矩阵
的关系。令常数
是矩阵
的秩,则
,当
时,很明显,矩阵
和矩阵
的大小不同,但矩阵
和矩阵
对角线上的非零元素却是相同的,若将矩阵
(或矩阵
)对角线上的非零元素分别为
,其中,这些特征值也都是非负的,再令矩阵
对角线上的非零元素分别为
,则
即非零奇异值的平方对应着矩阵(或矩阵
)的非零特征值,到这里,我们就不难看出奇异值分解与对称对角化分解的关系了,即我们可以由对称对角化分解得到我们想要的奇异值分解。
为了便于理解,在这里,给定一个大小为的矩阵
,虽然这个矩阵是方阵,但却不是对称矩阵,我们来看看它的奇异值分解是怎样的。
由进行对称对角化分解,得到特征值为
,
,相应地,特征向量为
,
;由
进行对称对角化分解,得到特征值为
,
,相应地,特征向量为
,
。取
,则矩阵
的奇异值分解为
.
若矩阵不再是一个方阵,而是一个大小为
的
,由
得到特征值为
,
,特征向量为
,
,
;由
得到特征值为
,
,特征向量为
,
,令
(注意:矩阵
大小为
),此时,矩阵
的奇异值分解为
.
比较有趣的是,假设给定一个对称矩阵,它是对称矩阵,则其奇异值分解是怎么样的呢?
分别计算和
,我们会发现,
,左奇异向量和右奇异向量构成的矩阵也是相等的,即
,更为神奇的是,该矩阵的奇异值分解和对称对角化分解相同,都是
。这是由于对于正定对称矩阵而言,奇异值分解和对称对角化分解结果相同。
3 奇异值分解的低秩逼近
在对称对角化分解中,若给定一个大小为的矩阵
,很显然,矩阵
的秩为
,特征值为
,
,
,对应的特征向量分别为
,
,
,考虑任意一个向量
,则
在这里,我们会发现,即使是一个任意向量,用矩阵
去乘以
的效果取决于
较大的特征值及其特征向量,类似地,在奇异值分解中,较大的奇异值会决定原矩阵的“主要特征”,下面我们来看看奇异值分解的低秩逼近(有时也被称为截断奇异值分解)。需要说明的是,接下来的部分是从文献《A Singularly Valuable Decomposition: The SVD of a Matrix》整理而来的。
给定一个大小为的矩阵
,由于
可以写成
其中,向量之间相互正交,向量
之间也相互正交,由内积
(有兴趣的读者可以自行推算)得到矩阵
的F-范数的平方为
知道了矩阵的F-范数的平方等于其所有奇异值的平方和之后,假设
是矩阵
的一个秩一逼近(rank one approximation),那么,它所带来的误差则是
(
是矩阵
的秩),不过如何证明
是最好的秩一逼近呢?
由于(证明过程见附录2),令
,其中,
是一个正常数,向量
和
分别是大小为
和
的单位向量,则
单独看大小为的矩阵
和
的内积
,我们会发现,
其中,需要注意的是,分别是向量
和
的第
个元素;向量
的大小为
,向量
的大小也为
,另外,以
为例,
是向量的模,则
(残差矩阵的平方和)为
当且仅当时,
取得最小值
,此时,矩阵
的秩一逼近恰好是
.
当然,我们也可以证明是矩阵
的最佳秩一逼近,以此类推,
是矩阵
的最佳秩一逼近。由于矩阵
的秩为
,这样,我们可以得到矩阵
的最佳秩
逼近(rank-
approximation),即
.
这里得到的矩阵的大小为
,矩阵
的大小为
,矩阵
的大小为
,矩阵
可以用
来做近似。
用低秩逼近去近似矩阵有什么价值呢?给定一个很大的矩阵,大小为
,我们需要存储的元素数量是
个,当矩阵
的秩
远小于
和
,我们只需要存储
个元素就能得到原矩阵
,即
个奇异值、
个左奇异向量的元素和
个右奇异向量的元素;若采用一个秩
矩阵
去逼近,我们则只需要存储更少的
个元素。因此,奇异值分解是一种重要的数据压缩方法。
另外,关于奇异值分解的应用将在该系列后续文章中进行详述。
---------------------------------------------------------------
附录1:相关链接:Largest eigenvalues of AA' equals to A'A,截图如下:
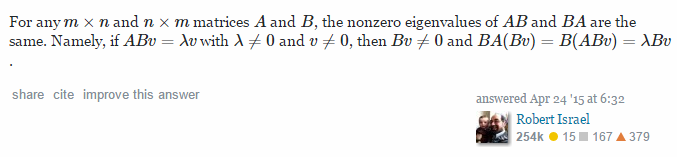
附录2:求证:,其中,
,
.
证明: