在这篇blog中我们一起来阅读一下 On the convergence of FedAvg on non-iid data 这篇 ICLR 2020 的paper.

主要目的

本文的主要目的是证明联邦学习算法的收敛性。与之前其他工作中的证明不同，本文的证明更贴近于实际联邦学习的场景。特别的，

1. 所有用户的数据non-iid分布；
2. 每次只有一部分用户参与FedAvg.

系统模型

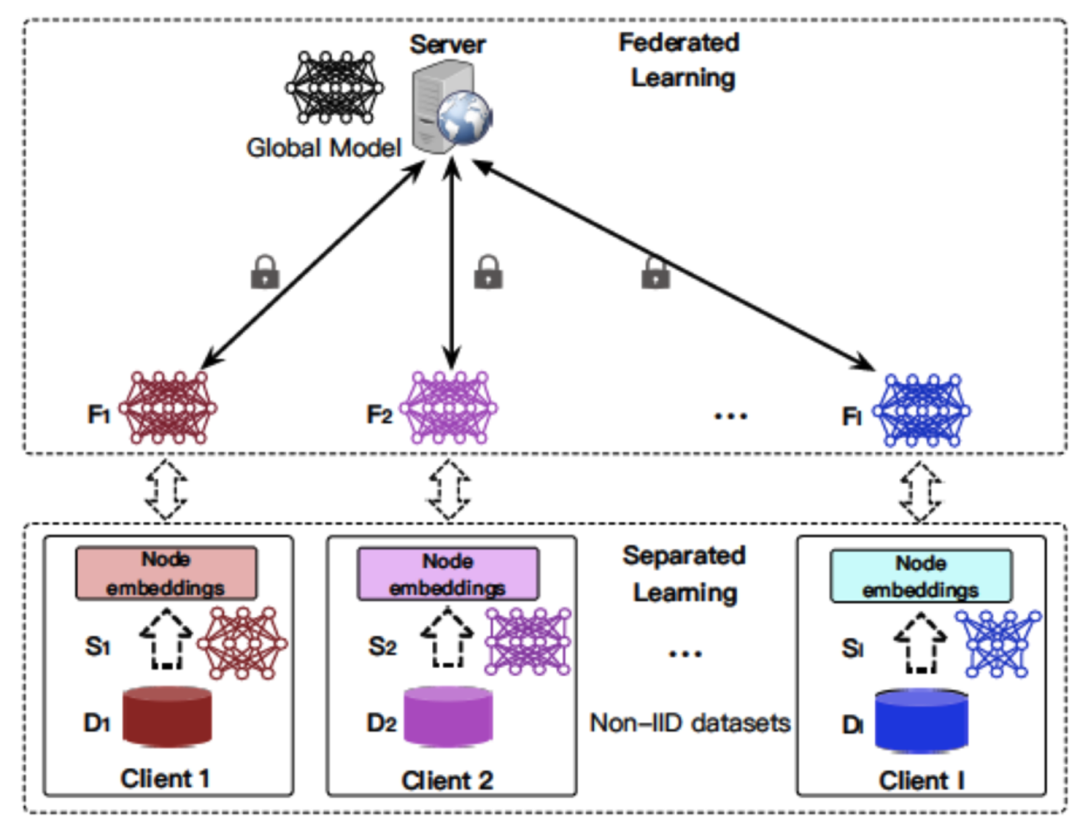
考虑一个联邦学习系统 with $N$ 用户和一个PS. 每用户有一些local data，训练发生在用户处，每隔一段时间用户上传自己学习的模型来做FedAvg.

将第 $k$ 个用户的数据记为 x = { x k , 1 , x k , 2 , x k , 3 , . . . , x k , n k } \bm{x}=\{x_{k,1},x_{k,2},x_{k,3},...,x_{k,n_k}\} x={xk,1​,xk,2​,xk,3​,...,xk,nk​​}, 每个人都有一个学习目标，即最小化 loss 函数
$$F_k(\mathbf{w})=\sum _{j=1}^{n_k}{\ell }_k(\mathbf{w},x_{k,j})\text{\hspace{1em}(1)}$$

其中 ${\ell }_k(\mathbf{w},x_{k,j})$ 是每个训练数据的 loss. $F_k(\mathbf{w})$ 相当于是每个人所有数据上的loss，如果仅仅做local training, 那最终每个用户会 arrive at
$$\text{Local minimum}:F_k^{\ast }=\underset{\mathbf{w}}{\min }{F}_k$$

而FL考虑的是一种分布式的优化，即我们要minimize的目标函数
$$\text{Global minimum}:F^{\ast }=\underset{\mathbf{w}}{\min }\sum _{k=1}^N{p}_k{F}_k(\mathbf{w})$$

其中 $p_k$ 是一个distribution用来表示每个用户所占的权重。换句话说，我们最终想找到一个共同的 $\mathbf{w}$ 来最小化每个用户 loss 的一个加权和。

To this end, 本文考虑FedAvg, 并证明其能收敛到 global optimum.

FedAvg 的具体步骤描述如下：首先，我们按单次SGD为一个时间刻度把时间轴分为离散的slot $t=1,2,3,...,T$, 即总共进行 $T$ 次 local SGD, 每次 SGD每个用户从自己的数据集中随机均匀的采样出一个数据来进行训练。特别的，每隔 $E$ slots, 所有 active users 把自己的本地参数发送给PS进行 FedAvg，之后PS会把avg后的参数发还给各个用户。以上模型用数学语言可以写为以下两步：

Local training

每个用户在第 $t$ 个时刻基于 ${\mathbf{w}}_t^k$ 进行 SGD, 得到
$${\mathbf{v}}_{t+1}^k={\mathbf{w}}_t^k-{\eta }_t\nabla {\ell }_k({\mathbf{w}}_t^k,{\xi }_t^k)\text{\hspace{1em}(2)}$$

其中 ${\xi }_t^k$ 是从本地数据中随机采样出的一个sample。注意，这样单步SGD得到的${\mathbf{v}}_{t+1}^k$ 只是一个中间变量而不是下一时刻的 ${\mathbf{w}}_{t+1}^k$，因为我们还有可能做 FedAvg。 更具体地说，在 $E$ 的非整数倍slot上，
w t + 1 k = v t + 1 k , if   t + 1 ∉ J E = { n E : n = 1 , 2 , . . . } . \bm{w}^k_{t+1}=\bm{v}^k_{t+1},~~~~\text{if}~~t+1\notin\mathcal{J}_E=\{nE:n=1,2,...\}. wt+1k​=vt+1k​,    if  t+1∈/​JE​={nE:n=1,2,...}.

而在 $E$ 的整数倍slot上，我们还得额外做 FedAvg.

FedAvg

若下一时刻是$E$的整数倍周期，即 t + 1 ∈ J E = { n E : n = 1 , 2 , . . . } t+1\in\mathcal{J}_E=\{nE:n=1,2,...\} t+1∈JE​={nE:n=1,2,...}，我们进行FedAvg，此时
$${\mathbf{w}}_{t+1}^k=\sum _{k=1}^N{p}_k{\mathbf{v}}_{t+1}^k\text{\hspace{1em}(3)}$$

注意，这里面我们假设每个人都参与更新，稍后我们会release这个条件允许PS按照某种分布采样一部分人进行更新。

小结

如果我们从每个用户的角度看，它的参数变化可以用下图归纳 ($E=3$)。

几个假设

本文的推导基于以下假设。

Assumption 1 ($L$-smoothness). 所有用户的 loss 函数 { F k : k = 1 , 2 , . . . , N } \{F^k:k=1,2,...,N\} {Fk:k=1,2,...,N} 都是 L-smooth.
$$F^k({\mathbf{x}}_2)-F^k({\mathbf{x}}_1)\le \nabla f({\mathbf{x}}_1{)}^{\top }({\mathbf{x}}_2-{\mathbf{x}}_1)+\frac{L}{2}\Vert {\mathbf{x}}_2-{\mathbf{x}}_1{\Vert }^2$$

Assumption 2 ($\mu$-strongly convex). 所有用户的 loss 函数 { F k : k = 1 , 2 , . . . , N } \{F^k:k=1,2,...,N\} {Fk:k=1,2,...,N} 都是 $\mu$-strongly convex.
$$F^k({\mathbf{x}}_2)-F^k({\mathbf{x}}_1)\ge \nabla f({\mathbf{x}}_1{)}^{\top }({\mathbf{x}}_2-{\mathbf{x}}_1)+\frac{\mu }{2}\Vert {\mathbf{x}}_2-{\mathbf{x}}_1{\Vert }^2$$

以上两个假设对 loss 函数的基本性质做了一些要求。即，函数变化的速度不会太快 ($L$-smooth) 也不会太慢 ($\mu$-strongly convex). 这两个假设下函数更详细的属性可参考 [1]. 等下证明时用到了哪个定义或者属性我们会再提及。

一般文献用这两个定义的原因是，我们可以把 bound "$F$ 和最优 $F^{\ast }$ 之间距离" 的问题转化为 bound "$w$ 和最优 ${\mathbf{w}}^{\ast }$ 之间距离" 的问题。即，只要明确了 $w$ 和 ${\mathbf{w}}^{\ast }$ 之间距离，就可以相应的把 $F$ 和 $F^{\ast }$ 之间的距离大概确定。

Assumption 3 (bounded variance of the stochastic gradients). 每个用户进行 SGD 时，其均匀采样的sample的随机梯度的 variance is bounded by ${\sigma }_k^2$:
$$\mathbb{E}\Vert \nabla {\ell }_k({\mathbf{w}}^k,{\xi }^k)-\nabla F^k(\mathbf{w}){\Vert }^2\le {\sigma }_k^2$$

Assumption 4 (bounded stochastic gradient). 每个用户的随机梯度的模值也是bounded:
$$\mathbb{E}\Vert \nabla {\ell }_k({\mathbf{w}}^k,{\xi }^k){\Vert }^2\le G^2$$

Full device participation

一些定义

作者首先证明了 FedAvg 在所有用户共同参与下的收敛性。

首先，基于上图 ${\mathbf{v}}^k$ 和 ${\mathbf{w}}^k$ 两个序列，我们定义两个虚拟序列
$${\bar{\mathbf{v}}}_t=\sum _{k=1}^N{p}_k{\mathbf{v}}_t^k,{\bar{\mathbf{w}}}_t=\sum _{k=1}^N{p}_k{\mathbf{w}}_t^k.$$

实际上这两个序列是 ${\mathbf{v}}^k$ 和 ${\mathbf{w}}^k$ 自身在所有用户上的加权和。特别的，${\bar{\mathbf{v}}}_t={\bar{\mathbf{w}}}_t$, 因为在非 $nE$ slot他们完全相等，在 $nE$ slot, 所有人的 ${\mathbf{w}}_{nE}^k$ 都是相等的且等于 ${\bar{\mathbf{v}}}_{nE}$, 即
$${\mathbf{w}}_{nE}^1={\mathbf{w}}_{nE}^2=...={\mathbf{w}}_{nE}^N={\bar{\mathbf{w}}}_{nE}={\bar{\mathbf{v}}}_{nE}$$.

而且，我们还可以把连续的两个 slots $t$ 和 $t+1$ 联系起来，因为我们知道
$${\mathbf{v}}_{t+1}^k={\mathbf{w}}_t^k-{\eta }_t\nabla \ell ({\mathbf{w}}_{\mathbf{t}}^{\mathbf{k}},{\xi }_t^k)\text{\hspace{1em}(4)}$$

定义单次SGD每个用户 gradient 的加权和
$${\mathbf{g}}_t=\sum _{k=1}^N{p}_k\nabla \ell ({\mathbf{w}}_{\mathbf{t}}^{\mathbf{k}},{\xi }_t^k)\text{\hspace{1em}(5)}$$

和单次steepest gradient descent (使用所有data) 每个用户 gradient 的加权和
$${\bar{\mathbf{g}}}_t=\sum _{k=1}^N{p}_k\nabla F^k({\mathbf{w}}_{\mathbf{t}})=\sum _{k=1}^N{p}_k\frac{1}{n_k}\sum _{j=1}^{n_k}\nabla \ell ({\mathbf{w}}_{\mathbf{t}}^{\mathbf{k}},x_{k,j})=\mathbb{E}[{\mathbf{g}}_t]\text{\hspace{1em}(6)}$$

其中 $\mathbb{E}$ averages over 所有用户选择的sample。

给定 ${\mathbf{g}}_t$, 我们可以把 (4) 两边用 $p_k$ 加权和
$${\bar{\mathbf{v}}}_{t+1}={\bar{\mathbf{w}}}_t-{\eta }_t{\mathbf{g}}_t\text{\hspace{1em}(7)}$$

Lemmas

我们跟随作者的思路，先证明一些 lemmas.

Lemma 1 (Results of one-step SGD). Assuming assumptions 1 and 2. If ${\eta }_t\le \frac{1}{4L}$, we have
$$\mathbb{E}\Vert {\bar{\mathbf{v}}}_{t+1}-{\mathbf{w}}^{\ast }{\Vert }^2\le (1-{\eta }_t\mu )\mathbb{E}\Vert {\bar{\mathbf{w}}}_t-{\mathbf{w}}^{\ast }{\Vert }^2+{\eta }_t^2\mathbb{E}\Vert {\mathbf{g}}_t-{\bar{\mathbf{g}}}_t{\Vert }^2+6L{\eta }_t^2\Gamma +2\mathbb{E}\sum _{k=1}^N{p}_k\Vert {\bar{\mathbf{w}}}_t-{\mathbf{w}}_k^t{\Vert }^2\text{\hspace{1em}(8)}$$

where $\Gamma =F^{\ast }-{\sum }_{k=1}^N{p}_k{F}_k^{\ast }\ge 0$.

Lemma 1 显然是很重要的，理解它对于后面的证明大有帮助。我们首先来看看其中的变量. 在某个slot $t$,

1. 每个用户的参数为 ${\mathbf{w}}_t^k$, 平均参数为 ${\bar{\mathbf{w}}}_t$ (averaged over all users).
2. 每个用户SGD更新的方向是 $\nabla \ell ({\mathbf{w}}_{\mathbf{t}}^{\mathbf{k}},{\xi }_t^k)$, 平均方向是 ${\mathbf{g}}_t^k$ (averaged over all users), 再 average over all data 的平均方向是 ${\bar{\mathbf{g}}}_t$.
3. 每个用户更新完后得到 ${\mathbf{v}}_{t+1}^k$, 平均参数是 ${\bar{v}}_{t+1}$ (averaged over all users).

因此，如果 $E=1$ 即每个时刻都做 FedAvg 的话，global 参数的演变历程其实就是 ${\bar{\mathbf{w}}}_t$ 沿着 ${\mathbf{g}}_t$ 的方向演变成 ${\bar{v}}_{t+1}$ 的过程：
$${\bar{\mathbf{w}}}_{t+1}={\bar{\mathbf{v}}}_{t+1}=\sum _{k=1}^N{p}_k{\mathbf{v}}_{t+1}^k=\sum _{k=1}^N{p}_k({\mathbf{w}}_t^k-{\eta }_t\nabla {\ell }_k)=\sum _{k=1}^N{p}_k{\mathbf{w}}_t^k-{\eta }_t\sum _{k=1}^N{p}_k\nabla {\ell }_k={\bar{\mathbf{w}}}_t-{\eta }_t{\mathbf{g}}_t$$

当 $E>1$ 时, 虽然我们并不是在每个时刻 averaging, 但是想象中这个平均的更新轨迹依然存在。而Lemma就是在bound这个平均运动轨迹每次更新后的 $\bar{\mathbf{v}}$ 与最优参数 ${\mathbf{w}}^{\ast }$ 的距离。

基于以上的定义，Lemma 1在干什么尼？显然，作者想基于 $t$ 时刻的所有信息预测经过一步SGD之后 ${\bar{\mathbf{v}}}_{t+1}$ 与 ${\mathbf{w}}^{\ast }$ 的距离。这个距离可以用以下4项来bound (分别对应Lemma 1中的4项):

1. $t$ 时刻，即SGD之前， ${\bar{\mathbf{w}}}_t$ 与 ${\mathbf{w}}^{\ast }$ 的距离；
2. 单步SGD的更新方向的variance；
3. heterogeneity $\Gamma$;
4. $t$ 时刻所有用户参数的variance。

Proof. 整个证明比较tedious，建议理解为重。

为了证明这个bound，我们从 (8) 式左侧开始推:

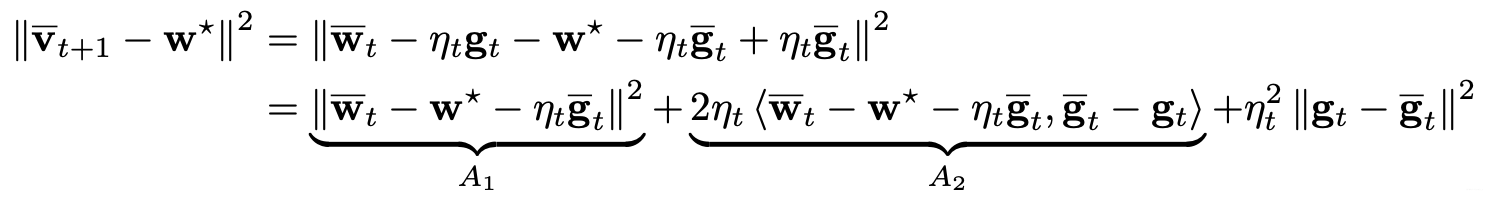
其中第一步直接由定义得出。特别的，作者引入了真实梯度 ${\bar{\mathbf{g}}}_t$ (gradient averaged over users and all data) 来替换掉随机梯度 ${\mathbf{g}}_t$ (stochastic gradient averaged only over users)，因为 ${\bar{\mathbf{g}}}_t$更好处理。第二步由向量模的基本运算得到 (想回顾的同学 [2] 中有)。特别的，因为$\mathbb{E}({\mathbf{g}}_t-{\bar{\mathbf{g}}}_t)=0$， 所以中间项 $A_2$ 的均值为0.

Bound $A_1$: $A_1$ 可以进一步写为

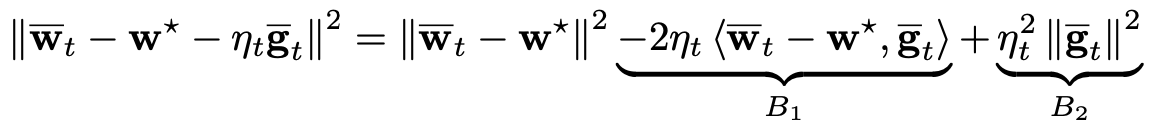
好，我们现在已经成功剥离出上一时刻的 ${\bar{\mathbf{w}}}_t$ 与 ${\mathbf{w}}^{\ast }$ 的距离了 (即第一项)。接下来继续 bound $B_1$ and $B_2$.

Bound $B_2$: $B_2$ 可以写为
$${\eta }_t^2\Vert {\bar{\mathbf{g}}}_t{\Vert }^2={\eta }_t^2{\Vert \sum _{k=1}^N{p}_k\nabla F_k({\mathbf{w}}_t^k)\Vert }^2\le {\eta }_t^2\sum _{k=1}^N{p}_k{\Vert \nabla F_k({\mathbf{w}}_t^k)\Vert }^2$$

因此我们需要 bound ${\Vert \nabla F^k({\mathbf{w}}_t^k)\Vert }^2$, 即任意一个用户 loss 函数 (所有数据的loss) 的梯度. 假设1和2中，我们用俩二次函数bound了每个用户loss的梯度 (即 $\mu$ strongly convex 和 $L$ smooth), 这里我们可以用 $L$ smoothness 来bound ${\Vert \nabla F^k({\mathbf{w}}_t^k)\Vert }^2$.
此式成立原因见 Definition 4.1 in [1]. 因此，$B_2$ 可以被 bound 为

Bound $B_1$: $B_1$ 可以写为

这里作者引入一个中间变量 ${\mathbf{w}}_t^k$。这样一来, 我们便可以从分析 ${\bar{\mathbf{w}}}_t-{\mathbf{w}}^{\ast }$ 转变为分析 ${\bar{\mathbf{w}}}_t-{\mathbf{w}}_t^k$ 和 ${\mathbf{w}}_t^k-{\mathbf{w}}^{\ast }$.

TBD.

Lemma 2. Assuming assumption 3, we have
$$\mathbb{E}\Vert {\mathbf{g}}_t-{\bar{\mathbf{g}}}_t{\Vert }^2\le \sum _{k=1}^N{p}_k^2{\sigma }_k^2$$

Lemma 3. Assume assumption 4. If ${\eta }_t$ is non-increasing and ${\eta }_t\le 2{\eta }_{t+E}$, then
$$\mathbb{E}\sum _{k=1}^N{p}_k\Vert {\bar{\mathbf{w}}}_t-{\mathbf{w}}_k^t{\Vert }^2\le 4{\eta }_t^2(E-1{)}^2{G}^2$$

Theorem 1: Convergence

将 Lemmas 2, 3 的结果代入 Lemma 1，我们即可得到
$$\mathbb{E}\Vert {\bar{\mathbf{w}}}_{t+1}-{\mathbf{w}}^{\ast }{\Vert }^2\le (1-{\eta }_t\mu )\mathbb{E}\Vert {\bar{\mathbf{w}}}_t-{\mathbf{w}}^{\ast }{\Vert }^2+{\eta }_t^{2}B\text{\hspace{1em}(9)}$$

其中
$$B=\sum _{k=1}^N{p}_k^2{\sigma }_k^2+6L\Gamma +8(E-1{)}^2{G}^2$$

换句话说，如果我们看 ${\bar{\mathbf{w}}}_t$ 这个虚拟序列，它距离最优 ${\mathbf{w}}^{\ast }$ 的距离可以由 (9) 式 recursively 刻画。那么下面我们唯一需要做的，就是证明这个距离序列是逐渐减小的即可。

令 ${\Delta }_t=\mathbb{E}\Vert {\bar{\mathbf{w}}}_t-{\mathbf{w}}^{\ast }{\Vert }^2$, (9) 式可简写为
$${\Delta }_{t+1}\le (1-{\eta }_t\mu ){\Delta }_t+{\eta }_t^{2}B$$

此式成立的两个条件: 1) ${\eta }_t\le \frac{1}{4L}$; 2) ${\eta }_t$ is non-increasing and ${\eta }_t\le 2{\eta }_{t+E}$. 下面，我们来选取一组符合这两个条件的 ${\eta }_t$ 来证明 ${\Delta }_t$ 是随时间逐渐减小的。

首先，选取 ${\eta }_t=\frac{\beta }{t+\gamma }$. 它是decreasing的，所以额外两个参数 $\beta ,\gamma$ 需要确保 ${\eta }_1=\frac{\beta }{1+\gamma }\le \frac{1}{4L}$ 和 $\frac{\beta }{t+\gamma }<2\frac{\beta }{t+E+\gamma }$ 才行。我们额外还希望 $0<{\eta }_1\mu <1$ 这样 ${\Delta }_t$ 前的系数就小于 $1$ 了.

先不给出$\beta ,\gamma$ 的具体取值，作者先用归纳法证明
Δ t ≤ v t + γ , v = max ⁡ { β 2 B β μ − 1 , ( γ + 1 ) Δ 1 } \Delta_t\leq\frac{v}{t+\gamma}, ~~~~v=\max\{\frac{\beta^2 B}{\beta\mu-1},(\gamma+1)\Delta_1\} Δt​≤t+γv​,    v=max{βμ−1β2B​,(γ+1)Δ1​}

1. $t=1$时，自然成立；
2. 假设任意时刻 $t$ 成立，则 $t+1$ 时刻
   $${\Delta }_{t+1}\le (1-{\eta }_t\mu ){\Delta }_t+{\eta }_t^{2}B$$

Reference

[1] https://blog.csdn.net/Lyn_S/article/details/119706754
[2] https://blog.csdn.net/Lyn_S/article/details/119744549