(1)基本组成

1.输入过程

• 顾客总体数量：有限or无限。
• 到达时间间隔：一般服从某一概率分布。
• 顾客行为假定：在未服务之前不会离开。

2.服务规则

• 服务台的数量，一个或多个。

3.数量指标

• 平均队长：排队系统中顾客数的平均值，$L_s$。
• 平均队列长：排队系统中等待服务的顾客数的平均值，$L_q$。
• 平均逗留时间：一个顾客在系统中停留的时间的平均值，$W_s$。
• 平均等待时间：一个顾客在系统中排队等待的时间的平均值，$W_q$。
• 稳态顾客数：$P_n$,表示当稳定时有$n$位顾客的概率。
• 平均到达率：单位时间内到达顾客的平均数$\lambda$。
• 平均服务率：单位时间内被服务顾客的平均数$\mu$。
• 服务强度：单位时间内的服务强度，$\rho =\frac{\lambda }{\mu }$。

(2)常见的分布

1.泊松分布

• 需要满足的条件：
  • 在$\Delta t$时间内，有一个顾客到达的概率为$\lambda \Delta t$ 。
  • 没有一个顾客到达的概率 $1-\lambda \Delta t$
  • 不可能多于一个顾客到达。
  • 注意这里直接将$\Delta t$视为无穷小量
• 顾客到达服从参数为$\lambda$的泊松流。

2.负指数分布

• 需要满足的条件：
  • 在$\Delta t$时间内，有一个顾客被服务完的概率为$\mu \Delta t$ 。
  • 没有一个顾客被服务完的概率 $1-\mu \Delta t$
  • 不可能多于一个顾客被服务完。
  • 注意这里直接将$\Delta t$视为无穷小量
• 服务时间服从参数为$\mu$。

(4)排队模型记号

• 一般形式：X/Y/Z/A/B/X
  • X顾客到达时间间隔分布。
  • Y服务时间分布。
  • Z服务台数目。
  • A排队系统允许的最大顾客容量。
  • B顾客总体数量。
  • C排队规则(一般情况为先到先服务)。

(5)单服务台模型

0.Little公式

• 运行指标之间的关系：
  • $L_s=\lambda W_s$
  • $L_q=\lambda W_q$
  • $L_s=L_q+\frac{\lambda }{\mu }$
  • $W_s=W_q+\frac{1}{\mu }$

1.标准型M/M/1/$\infty$/$\infty$

• 特点：
  • 顾客源为无限的，顾客的到达相互独立，到达规律服从参数为$\lambda$的泊松分布。
  • 单服务台、队长无限、先到先服务。
  • 各顾客的服务时间相互独立，且同服从于参数为$\mu$的负指数分布。
• 首先计算出来对应的P值：
  $$\begin{gathered} P_0=1-\rho \\ {P}_n=(1-\rho ){\rho }^n \end{gathered}$$
• 计算出的参数结果：
  $$\begin{gathered} 平均队长：L_s=\frac{\lambda }{\mu -\lambda } \\ 平均队列长：L_q=\frac{\rho \lambda }{\mu -\lambda } \\ 平均逗留时间：W_s=\frac{1}{\mu -\lambda } \\ 平均等待时间：W_q=\frac{\rho }{\mu -\lambda } \end{gathered}$$

2.系统容量有限型M/M/1/N/$\infty$

• 损失制:当顾客到达时，所有的服务台均被占用，顾客随即离去。
• 首先计算出来对应的P值：

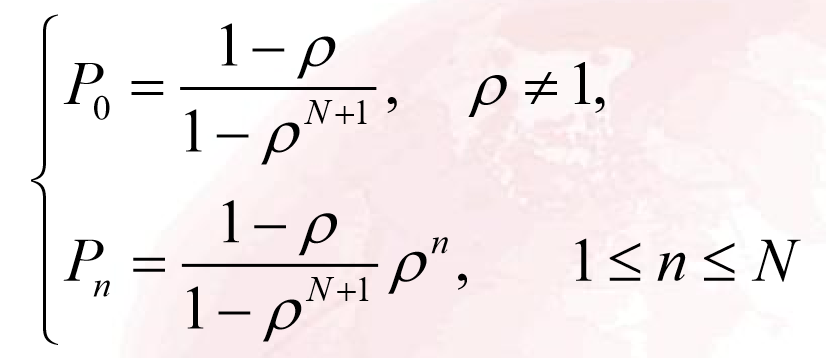
• 计算出的参数结果：
  $$\begin{gathered} 有效到达率：{\lambda }_e=\lambda (1-P_N) \\ 有效服务强度：\frac{{\lambda }_e}{\mu }=1-P_0 \\ 平均队长：L_s=\frac{1}{1-\rho }-\frac{(N+1){\rho }^{N+1}}{1-{\rho }^{N+1}}(\rho \ne 1,当\rho =1时说明流入和流出相等，没有排队现象产生) \\ 平均队列长：L_q=L_s-(1-P_0) \\ 平均逗留时间：W_s=\frac{L_s}{{\lambda }_e}=\frac{L_s}{\lambda (1-P_N)}=\frac{L_q}{\lambda (1-P_N)}+\frac{1}{\mu } \\ 平均等待时间：W_q=\frac{L_q}{{\lambda }_e}=\frac{L_q}{\lambda (1-P_N)}=W_s-\frac{1}{\mu } \end{gathered}$$

3.顾客源有限型M/M/1/$\infty$/m

• 首先说明一下，因为顾客源只有m，所以最多的情况就是来m个顾客，因此这个模型和 M/M/1/m/m 其实是完全一样的。
• 注意这里的$\lambda$的定义和前面有一些区别，这里的$\lambda$定义为单位时间内该顾客来到系统请求服务的次数。
• 首先计算出来对应的P值：

• 计算出的参数结果：
  $$\begin{gathered} 平均队长：L_s=m-\frac{\mu }{\lambda }(1-P_0) \\ 平均队列长：L_q=m-\frac{(\lambda +\mu )(1-P_0)}{\lambda }=L_s-(1-P_0) \\ 平均逗留时间：W_s=\frac{m}{\mu (1-P_0)}-\frac{1}{\lambda } \\ 平均等待时间：W_q=W_s-\frac{1}{\mu } \end{gathered}$$

(6)多服务台模型

1.多服务台标准型M/M/c/

• 顾客流为泊松流，平均到达率为$\lambda$,各个服务台的平均服务率是$\mu$。

• 整个服务机构的平均服务率为 $n\mu (n<c)$ 或 $c\mu (n\ge c)$。

• 系统服务强度为（当$\rho >1$时会产生排队现象）$$\rho =\frac{\lambda }{c\mu }$$

• 首先计算出来对应的P值：

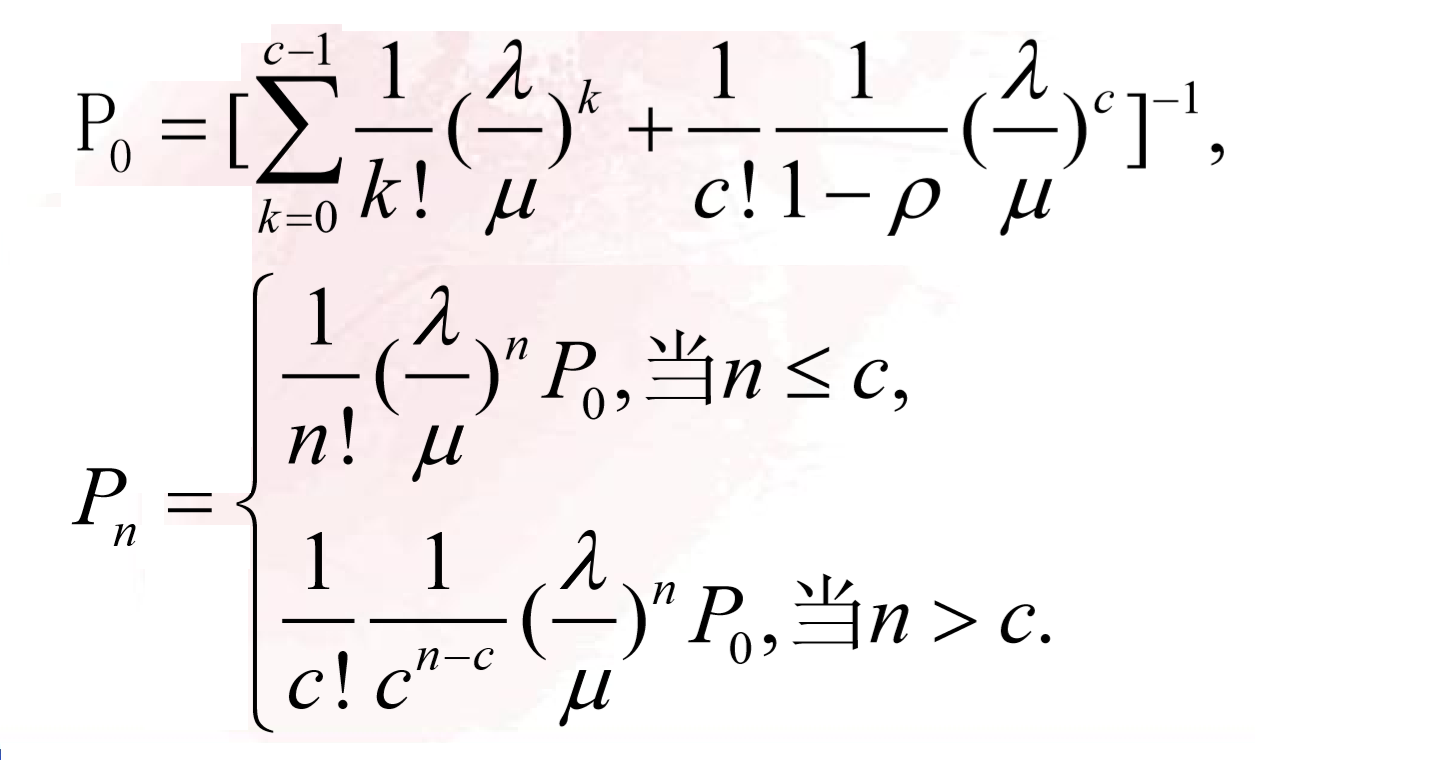
• 计算出系统的运行指标：

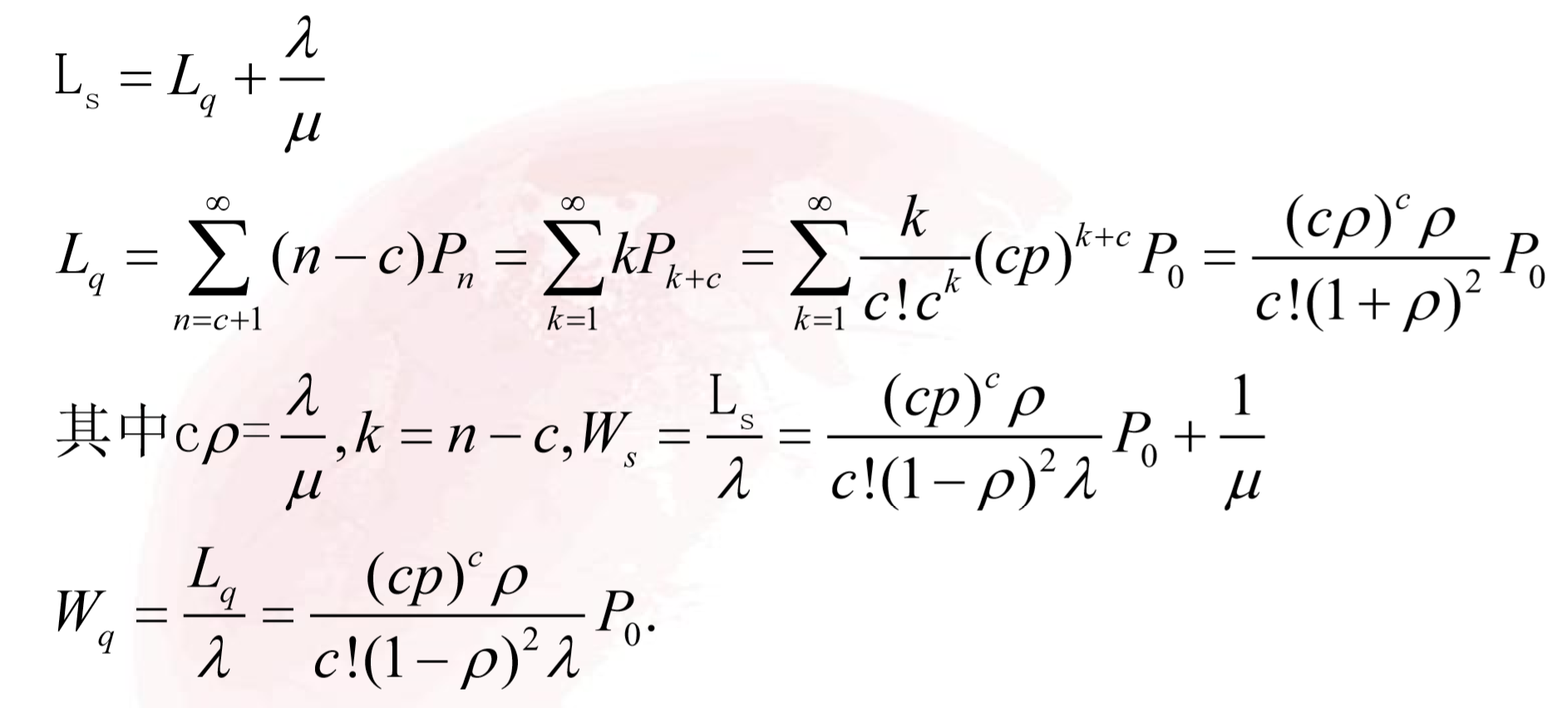
• 一个有用的结论：
  顾客逗留时间服从 $\mu -\lambda$ 的指数分布(参考平均逗留时间$W_s$)。

2.多服务台M/M/c/N/$\infty$

• 首先计算出来对应的P值：

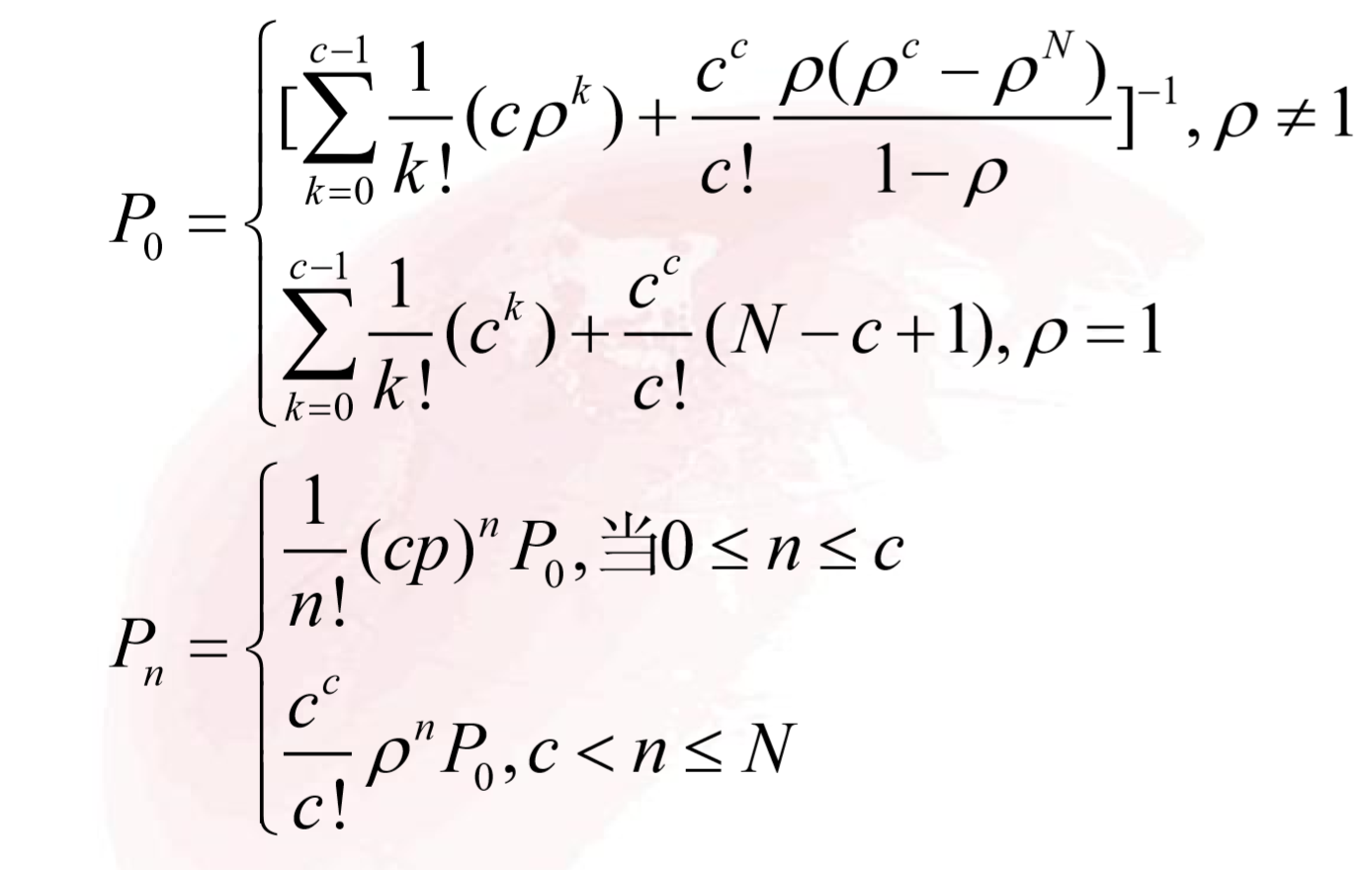
• 计算出系统的运行指标：

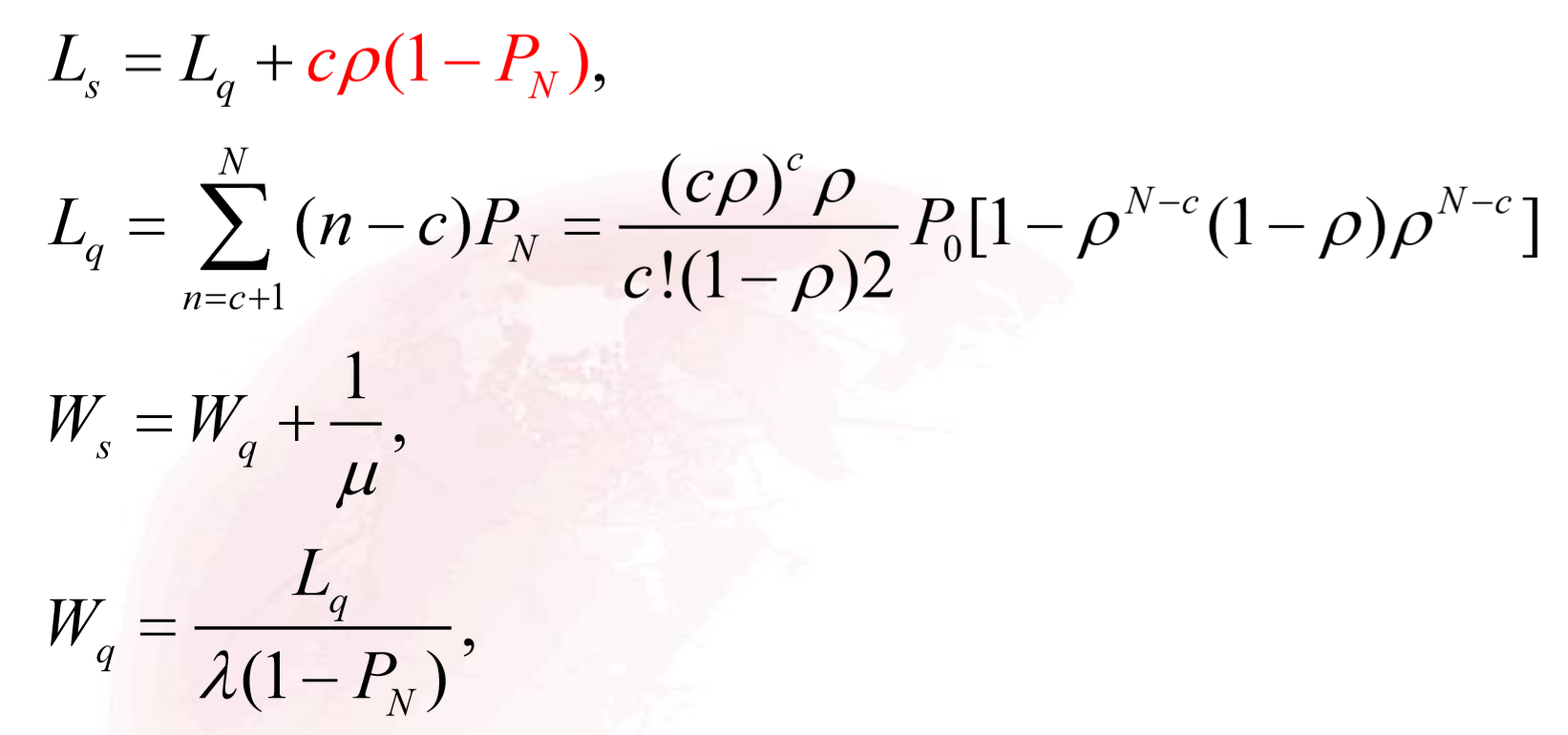
3.多服务台M/M/c/$\infty$/m

• 首先计算出来对应的P值：

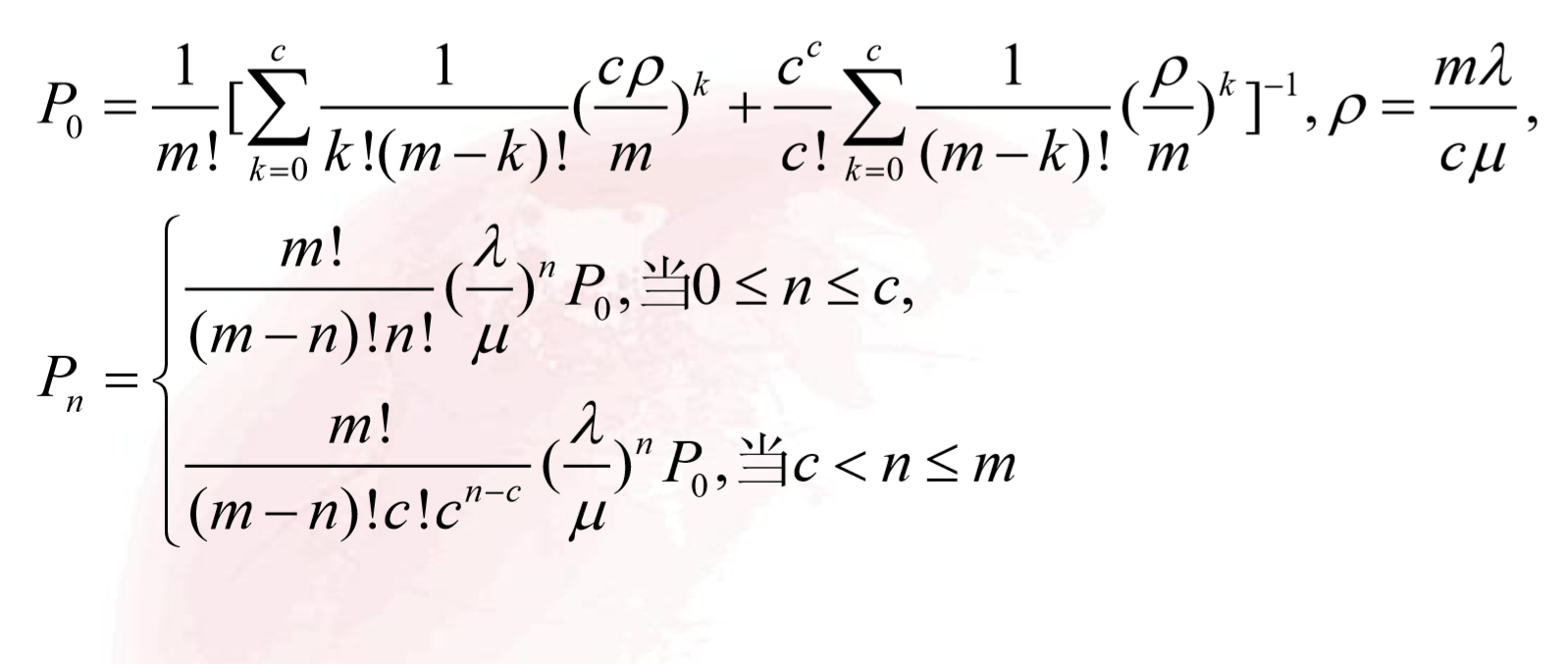
• 计算出系统的运行指标：

(7)排队系统最优化

1.标准M/M/1系统的最优服务率

• 参数引入：
  • $C_s$:对每个顾客的单位时间服务费。
  • $C_w$:为每个顾客在系统停留单位时间的损失费。
  • $G$:单位时间对每位顾客服务的收入。
  • $z$:总费用。
• 优化目标(单位时间费用最小)：$\min z=C_s\mu +C_w{L}_s$
• 求得最优取值：$${\mu }^{\ast }=\lambda +\sqrt{\frac{C_w}{C_s}\lambda }$$
• 优化目标(服务利润最大)：$\max z=\mu (1-P_0)G-C_s\mu$ ($1-P_0$表示排除没有人的情况)

2.系统容量有限M/M/1/N/$\infty$的最优服务率

• 与标准情况的差别：这里相当于如果系统中已经有$N$个顾客了，那么后来的都会被拒绝，所以说这里实际进入(稳定状态下服务完)的客户多一个$(1-P_N)$的系数，为$\lambda (1-P_N)$。
• 优化目标为：$$\min z=\lambda (1-P_N)G-C_s\mu =\lambda G\frac{1-{\rho }^N}{1-{\rho }^{N+1}}-C_s\mu$$
• 求得结果：
  $${\rho }^{N+1}\frac{N-(N+1)\rho +{\rho }^{N+1}}{(1-{\rho }^{N+1}{)}^2}=\frac{C_s}{G}$$
  注意这里面$\rho =\frac{\lambda }{\mu }$，其他的参量也都知道，因此最后只需要通过数值方法求解${\mu }^{\ast }$。

3.顾客源有限M/M/1/m/m的最优服务率

• 根据之前的模型可知，单位时间服务完的顾客数为$\lambda (m-L_s)$。
• 优化目标(服务利润最大)：$\max z=\lambda (m-L_s)G-C_s\mu$ ($1-P_0$表示排除没有人的情况)
• 优化结果为：

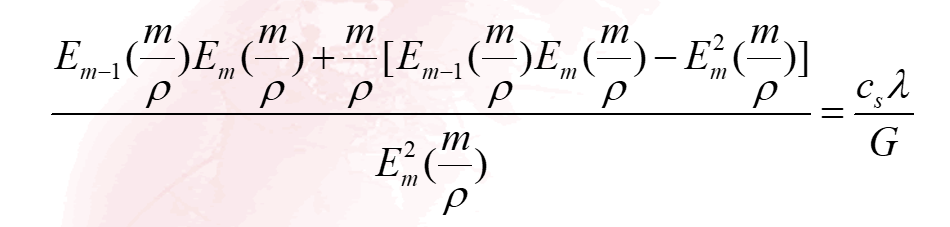
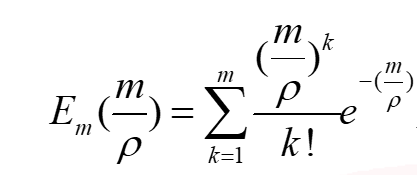
4.标准M/M/c的最优服务台数

• 优化目标(单位时间费用最小)：$\min z=C_s\mu +C_w{L}_s$，注意这里因为$L_s=L_s(c)$所以个服务台的个数有关。
• 由于$c$是离散的取值，因此采用边际分析法求解，假定$c$的最优值为$c^{\ast }$，此时$z(c^{\ast })$为最少费用。
• 根据最小值的特性可以得到如下的不等式：
  $$\begin{gathered} z(c^{\ast })\le z(c^{\ast }-1) \\ z(c^{\ast })\le z(c^{\ast }+1) \end{gathered}$$
• 化简得到结果：

现在已经转移到知乎，之后的文章会在知乎更新。