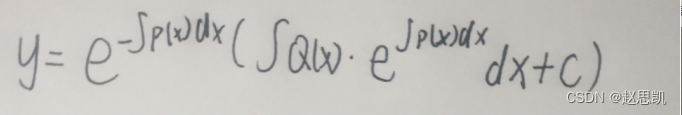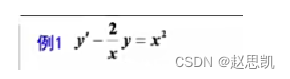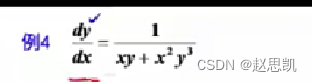目录
线性方程
例题:
伯努利方程
例题:
编辑
线性方程

我们先对齐次方程进行求解:
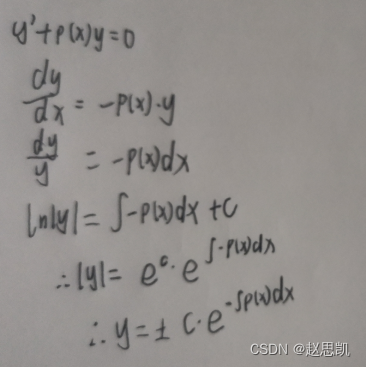
所以一阶线性微分齐次方程的公式:

那么对于非齐次的方程,我们该怎么求解呢?
我们可以把这里的任意数c换成一个函数,用这个函数来代替Q(x)
这就叫做常数变易法。

所以一阶非齐次线性微分方程的通解是:
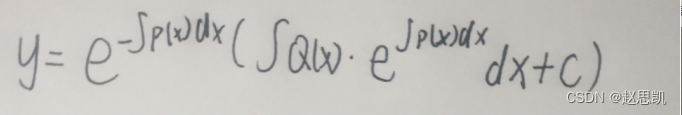
例题:
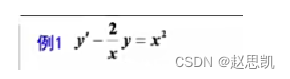


伯努利方程


例题:

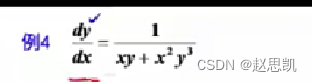

目录
线性方程
例题:
伯努利方程
例题:
编辑

我们先对齐次方程进行求解:
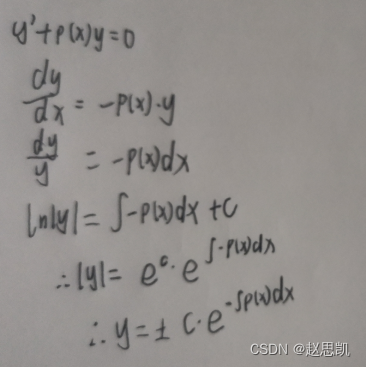
所以一阶线性微分齐次方程的公式:

那么对于非齐次的方程,我们该怎么求解呢?
我们可以把这里的任意数c换成一个函数,用这个函数来代替Q(x)
这就叫做常数变易法。

所以一阶非齐次线性微分方程的通解是: