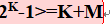海明校验码
视频链接地址:
https://www.bilibili.com/video/BV1BE411D7ii?from=search&seid=6420326887479343502
前言
在本篇中,你将掌握
海明码的基本思想
海明码的求解步骤和全校验码

在计算机内部进行存储、计算的数据都是以二进制形式传送,由于计算机元器件或环境噪音干扰有可能导致计算机内部二进制数据发生错误,所以我们必须考虑这种错误
1 海明码的基本思想
奇偶校验码:1位奇偶校验位 + n位有效信息位
对于上篇的奇偶校验码有这样的问题:如偶校验码只能校验奇数位错误,但无法确定是哪一位出错。
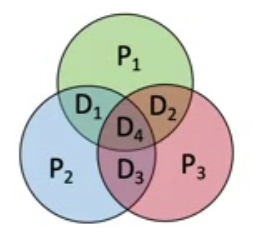
而海明码设计思路:将信息位分组进行偶校验 得到 多个校验位,多个校验位标注出出错位置。
1.1 需要多少个校验位
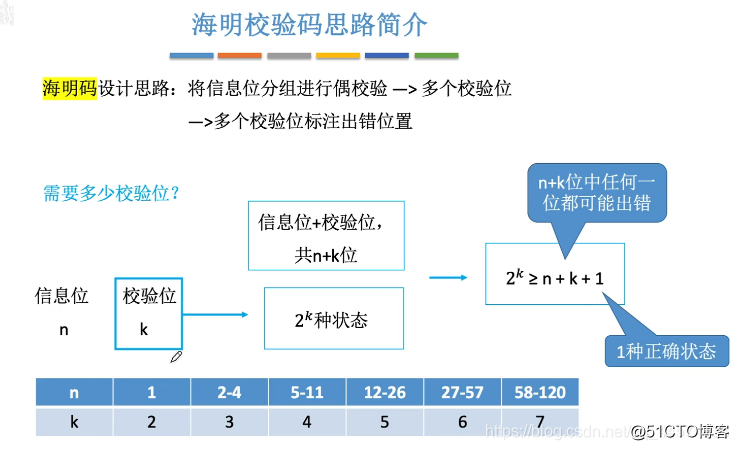
海明校验码的组成是 n位信息位 + k位校验位,那我们需要多少个校验位呢?
首先,k个校验位能够校验表示2
k
2^k2k种状态;而信息位+校验位共有n+k位,这n+k个位都有可能出错,所以这2
k
2^k2k种状态中显然需要包括n+k +1种情况(正确状态),即
2
k
>
=
n
+
k
+
1
2^k >= n+k+12k>=n+k+1
对于n,k的对应关系如上图表格,当然也可以手动计算找出k的最小值。
1.2 海明码求解步骤

对于信息位:1010,让我们来一下它的海明码该怎么求?
根据不等式2
k
>
=
n
+
k
+
1
2^k >= n+k+12k>=n+k+1确定海明码的校验位个数k,并用D
4
,
D
3
,
D
2
,
D
1
D_4,D_3,D_2,D_1D4,D3,D2,D1表示信息位,用P
3
,
P
2
,
P
1
P_3,P_2,P_1P3,P2,P1表示校验位,其海明码应为H
7
,
H
6
,
H
5
,
H
4
,
H
3
,
H
2
,
H
1
H_7,H_6,H_5,H_4,H_3,H_2,H_1H7,H6,H5,H4,H3,H2,H1
确定校验位的分布,根据校验位P
i
P_iPi放在海明码号为2
i
−
1
2_{i-1}2i−1的位置上,信息位按顺序放到其他位置
就比如P
2
P_2P2就会被放到2
2
−
1
=
2
2^{2-1} = 222−1=2的H
2
H_2H2位置上
求校验位的值
将信息位的D
4
,
D
3
,
D
2
,
D
1
D_4,D_3,D_2,D_1D4,D3,D2,D1所在位置用二进制数表示
如D
1
=
H
3
=
3
=
011
D_1 = H_3 = 3 = 011D1=H3=3=011
和D
2
=
H
5
=
5
=
101
D_2 = H_5 = 5 = 101D2=H5=5=101
和D
3
=
H
6
=
6
=
110
D_3 = H_6 = 6 = 110D3=H6=6=110
和D
4
=
H
7
=
7
=
111
D_4 = H_7 = 7 = 111D4=H7=7=111
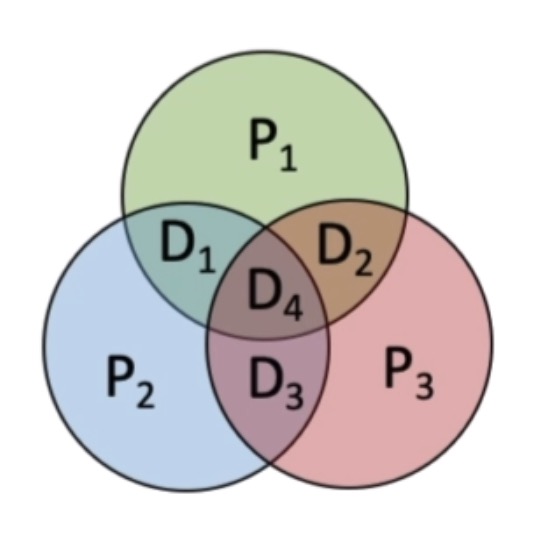
则各个分组的P
i
P_iPi便是对应二进制位的i位为1的信息位的异或和
如P
1
=
D
1
异
或
D
2
异
或
D
4
=
0
异
或
1
异
或
1
=
0
P_1 = D_1 异或 D_2 异或 D_4 = 0 异或 1 异或1 = 0P1=D1异或D2异或D4=0异或1异或1=0
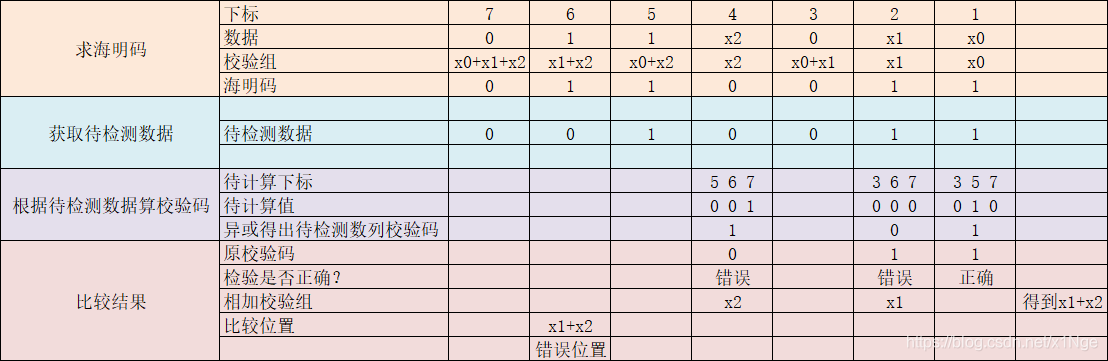
4.纠错
纠错的方法便是校验每一组的异或值是否为1,若为1则海明码出错,且出错位置为S
1
,
S
2
,
S
3
S_1,S_2,S_3S1,S2,S3这三组表示的二进制数转成十进制的位置,如接收到的1010010计算得到的S
1
,
S
2
,
S
3
S_1,S_2,S_3S1,S2,S3 = 010 = 2,代表第2个位置出错
注意!:要注意给出的信息位是D
4
,
D
3
,
D
2
,
D
1
D_4,D_3,D_2,D_1D4,D3,D2,D1还是D
1
,
D
2
,
D
3
,
D
4
D_1,D_2,D_3,D_4D1,D2,D3,D4,上述例子是从大到小的信息位排列,但原理上是一样的
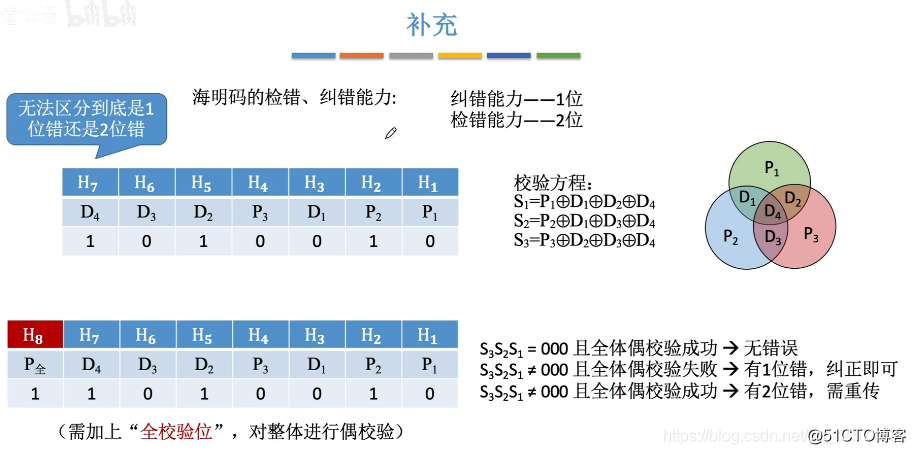
补充:海明码的检错、纠错能力
检错能力——2位
纠错能力——1位
为了避免两位错误导致无法区分,因此一般海明码还会加上“全校验位”,对整体进行偶校验,方法如上图,根据分组校验的S
3
,
S
2
,
S
1
S_3,S_2,S_1S3,S2,S1结果与全体偶校验来判断出错个数
2 小结
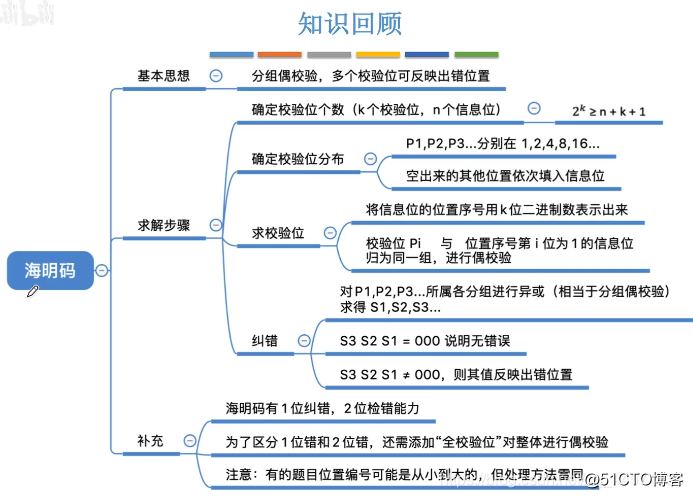
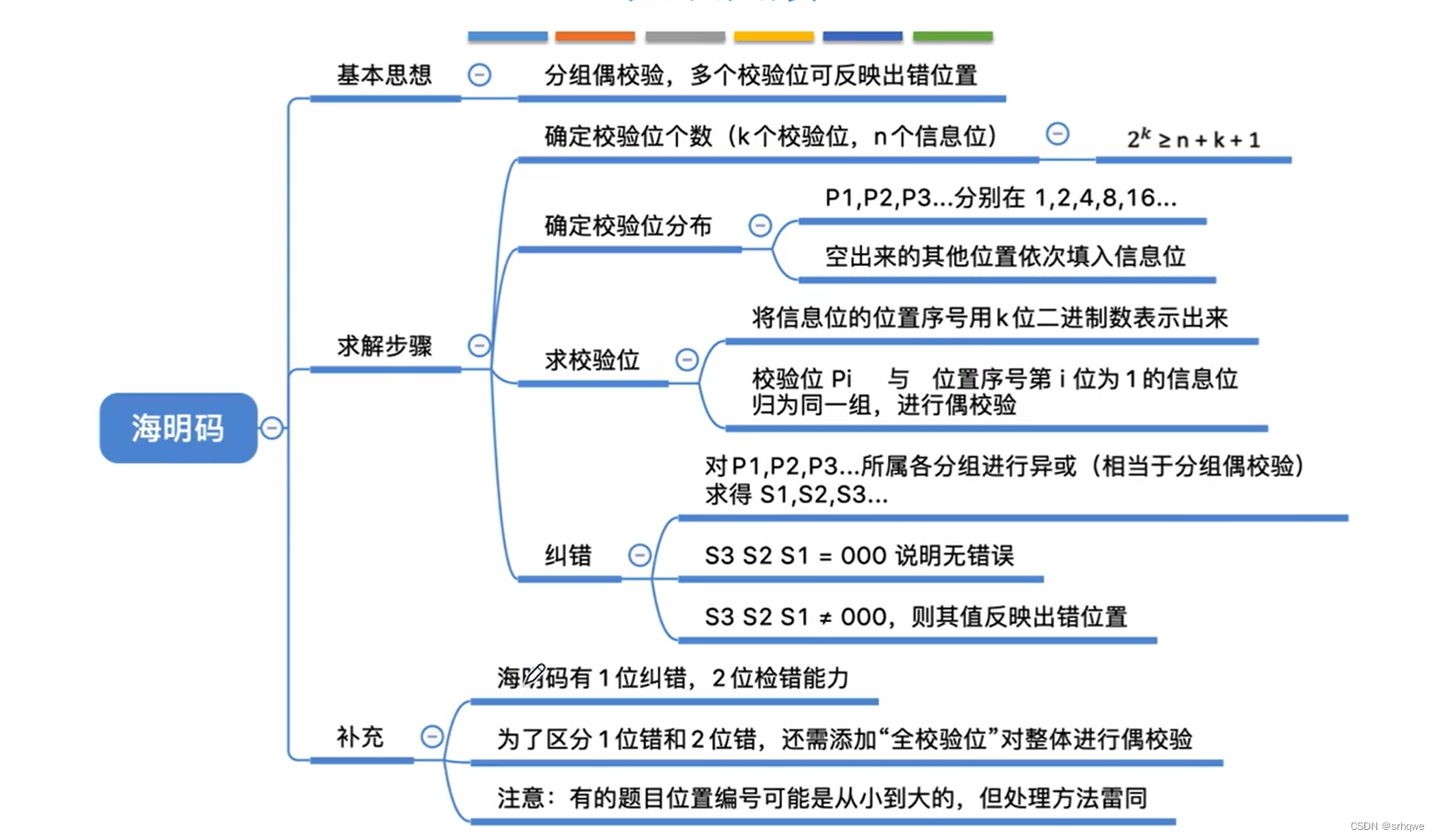
本篇重点,海明码的求解过程:确定校验位个数——确定校验位分布——求校验位——纠错,全校验位如何区分错1位还是2位。
海明码既是计算机组成原理的重点,又是计算机网络的重点,请仔细理解。