海明校验码原理以及作用机制的介绍

什么是海明校验码？

由Richard Hamming于1950年提出、还被广泛采用的一种很有效的校验方法，是只要增加少数几个校验位，就能检测出二位同时出错、亦能检测出一位出错并能自动恢复该出错位的正确值的有效手段，后者被称为自动纠错。

它的实现原理，是在k个数据位之外加上r个校验位，从而形成一个k+r位的新的码字，使新的码字的码距比较均匀地拉大。把数据的每一个二进制位分配在几个不同的偶校验位的组合中，当某一位出错后，就会引起相关的几个校验位的值发生变化，这不但可以发现出错，还能指出是哪一位出错，为进一步自动纠错提供了依据。（来源百度百科）

简单地说：海明校验码是一种能够纠正一位错误，检测两位错误并且能够自动恢复出错位的校验码。

编码原则：

假设数据位的位数为 k 位，校验位数为 r 位，在编制海明码的时候，需要满足海明不等式： $2^{r}\geqslant k+r+1$ 。也可以理解为信息位为k位，增加r位冗余位，构成一个n＝k＋r位的码字，则海明不等式又可以表达为： $2^{r}\geqslant n+1$ 。

在海明不等式—— $2^{r}\geqslant k+r+1$ 中，1是表示用其中的一个状态信息表示没有发生错误，其余的状态信息用于指出错误并且发生在哪一位，又因为检验位也可能发生错误，所以是 k+r 个。（在这里讲明一下，因为海明校验码在设计之初就是能够发现并纠正一位错误，所以你在看这个不等式时要带着发生一位错误的角度去看待！）

数据位和校验位的对应关系表：

信息码位数	1	2~4	5~11	12~26	27~57	58~120
校验码位数	2	3	4	5	6	7

但是在实际运用中应该是 $2^{r-1}\geqslant k+r+1$ ，详情请看评论区的解释！再次感谢—猫猫官人—提出的问题！(*^_^*)

信息码位数	1-3	4-10	11-25	26-56	57-119
校验码位数	4	5	6	7	8

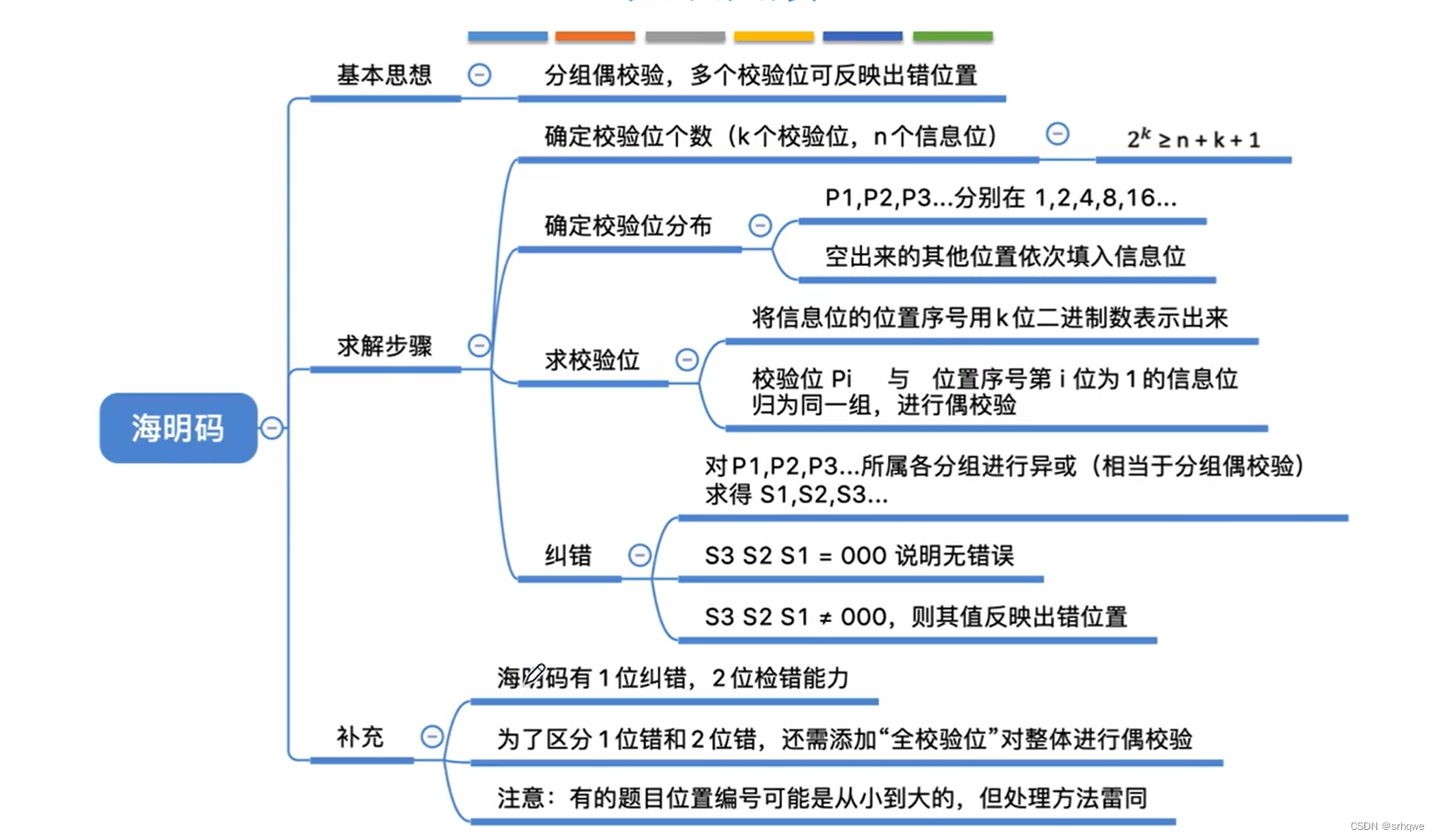
海明码编制的基本规则：

假设海明码的最高位的位号为m，最低位号为1，海明码为Hm Hm-1 ··· H1。海明码的编码规则如下：

（1）校验位与数据位个数之和为m，每个校验位Pi在海明码中被分在位号为 $2^{i-1}$ 的位置上，其余各位为数据位Di，并按照从低到高逐位依次安排各个数据位。

（2）海明码的每一位码（包括数据位和校验位本身）由多个校验位进行校验，其关系是被校验的每一位位号要等于校验它的各校验位的位号之和。

（3）在增大合法码的码距时，使得所有的码距尽量均匀的增大，以保证对所有码的验错能力平衡提高。

那么什么是码距呢？

码距：任何一种编码都是由码字构成的，任何两个码字之间最少变化的二进制位数，被称为“数据校验码的码距”。

——码距大于等于二的数据校验码，才开始具有检错能力。码距越大，检错纠错能力就越强，但是无论怎么变化，检错能力总是大于等于纠错能力的。

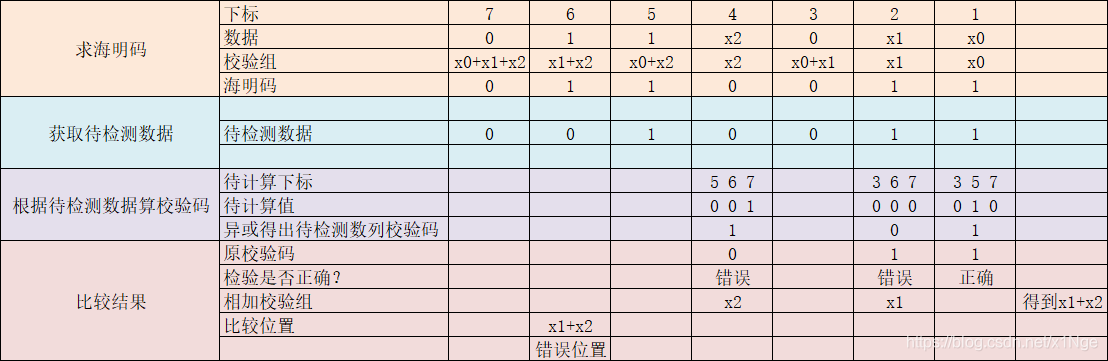
举例说明：为一个8位的二进制数编海明码。

解：根据海明码不等式 $2^{r-1}\geqslant k+r+1$ ，在这个题目中数据位数k=8，所以校验位数r=5，所以海明码的位数为k+r=13。

海明码： $H_{13}H_{12}H_{11}H_{10}H_{9}H_{8}H_{7}H_{6}H_{5}H_{4}H_{3}H_{2}H_{1}$

根据规则一：校验位与数据位个数之和为m，每个校验位Pi在海明码中被分在位号为 $2^{i-1}$ 的位置上，其余各位为数据位Di，并按照从低到高逐位依次安排各个数据位。

根据该规则可知，校验位Pi应当放置在1，2，4，8，16的位置上，但是由于海明码一共才13位，所以本应该放置在第16位置上的校验位实际放置在第13位上。

$H_{13}H_{12}H_{11}H_{10}H_{9}H_{8}H_{7}H_{6}H_{5}H_{4}H_{3}H_{2}H_{1}$ 各位对应为——> $P_{5}D_{8}D_{7}D_{6}D_{5}P_{4}D_{4}D_{3}D_{2}P_{3}D_{1}P_{2}P_{1}$

根据规则二：海明码的每一位码（包括数据位和校验位本身）由多个校验位进行校验，其关系是被校验的每一位位号要等于校验它的各校验位的位号之和。

出错的海明码号和校验位位号的关系：

海明码位号	数据位校验位	参与校验的校验位位号	被校验位的海明码位号=校验位位号之和
H1	P1	1	1=1
H2	P2	2	2=2
H3	D1	1,2	3=1+2
H4	P3	4	4=4
H5	D2	1,4	5=1+4
H6	D3	2,4	6=2+4
H7	D4	1,2,4	7=1+2+4
H8	P4	8	8=8
H9	D5	1,8	9=1+8
H10	D6	2,8	10=2+8
H11	D7	1,2,8	11=1+2+8
H12	D8	4,8	12=4+8
H13	P5	13	13=13

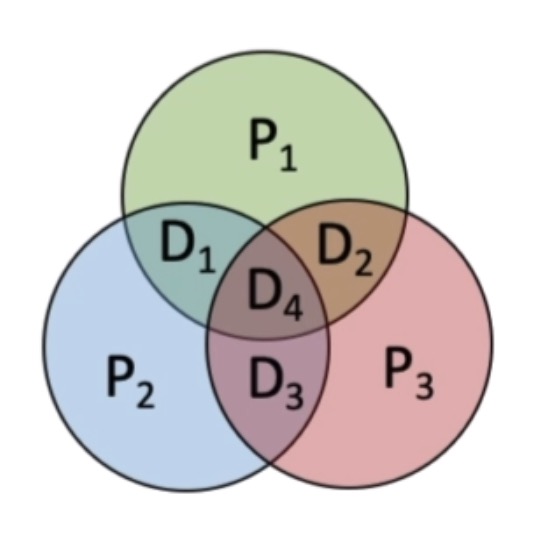
通过观察上面的表格，我们可以发现，5个校验位只与本身有关，数据位则与多个校验位有关。D1由P1和P2校验、D3由P2和P4校验... ...

P1校验D1、D2、D4、D5、D7
P2校验D1、D3、D4、D6、D7
P3校验D2、D3、D4、D8
P4校验D5、D6、D7、D8

其中D4和D7都出现了三次，其余的数据位置出现了两次，这就说明对于每一个数据位的校验能力是不均衡的（不符合规则三的要求），为了平衡一下，因此我们增添P5。

P5校验D1、D2、D3、D5、D6、D8

就此我们可以得出一个结论：当一位数据位Di发生变化时，必将引起三个校验位Pi的变化，即合法的海明码的码距都为4。

根据上面的校验关系，我们写出校验位的偶校验方程：

那么什么是偶校验呢？

奇偶校验码：

——发送方：附加1位冗余位，使码字中“1”的个数保持为奇数或偶数。

——接收方：根据所收到的码字中“1”的个数是奇数或偶数判别是否有传输差错。

所以偶校验就是附加1位冗余位，使得码字中“1”的个数保持偶数个。奇校验就是附加一位冗余位，使得码字中“1”的个数保持奇数个。

（来源自我的之后的博客！）

偶校验方程：（⊕为异或符号）（其实这里取巧了，因为当“1”的个数是偶数个时，经过异或运算之后结果就为0了。）

P1=D1⊕D2⊕D4⊕D5⊕D7

P2=D1⊕D3⊕D4⊕D6⊕D7

P3=D2⊕D3⊕D4⊕D8

P4=D5⊕D6⊕D7⊕D8

P5=D1⊕D2⊕D3⊕D5⊕D6⊕D8

那么我要是进行奇校验，那怎么书写奇校验方程呢？

在原方程的基础上加上一个⊕1就好了，譬如上面的P1就变成了P1=D1⊕D2⊕D4⊕D5⊕D7⊕1。

你要是觉得这个花里胡哨，那来一点实在一点的，直接按照奇偶校验的原理来求解校验位的取值！

假设要传送的数据为：10110110，那么：

P1校验D1、D2、D4、D5、D7
P2校验D1、D3、D4、D6、D7
P3校验D2、D3、D4、D8
P4校验D5、D6、D7、D8

P1对应的校验数据为01010（75421），如果是偶校验，01010中“1”的数目为偶数个，所以P1=0；如果是奇校验，01010中“1”的数目为偶数个，所以为了凑足奇数个，所以P1=1。

P3对应的校验数据为1011（8432），如果是偶校验，1011中“1”的数目为奇数个，所以为了凑足偶数个，所以P3=1；如果是奇校验，1011中“1”的数目为奇数个，所以P3=0。

接下来看看海明码如何进行检错和纠错的！

检错和纠错机制：

假设发送端发送的数据为D8~D1，海明校验位的取值就是P1、P2、P3、P4、P5,；在数据接收端，接收到的海明校验码为 $P_{1}^{`}$ 、 $P_{2}^{`}$ 、 $P_{3}^{`}$ 、 $P_{4}^{`}$ 、 $P_{5}^{`}$ 。

令：S1= $P_{1}^{`}$ ⊕P1、S2= $P_{2}^{`}$ ⊕P2、S3= $P_{3}^{`}$ ⊕P3、S4= $P_{4}^{`}$ ⊕P4、S5= $P_{5}^{`}$ ⊕P5。

当S1~S5全为零时，表示无错。（因为S1~S5都为零，表示 $P_{1}^{`}$ ~ $P_{5}^{`}$ 和P1~P5完全相同；说明接收端和发送端的数据完全一样，没有发生错误。）
当S1~S5中仅有一位不为0时，说明有一个校验位出错。
当两位不为零时，表示两位海明码出错。
当三位不为零时，表明一个数据位出错。出错的海明码位号由S4~S1四位的编码值得出。（因为一个数据位的变化必将引起三个校验位的变化，所以当三位不为零时，就表明一定有一个数据位出错了。）
当中有4位或5位不为0时，表明出错情况严重，系统可能出现故障，应该检查系统硬件的正确性。

举例说明：如果要传送的数据为：10110110，请编写海明码。

根据校验方程求得：P1=0，P2=0，P3=1，P4=1，P5=1；所以，海明码为1101110111000。

假设在传送过程中发生了错误，接收方接收到得数据为10111110，D4位由0变成了1，发生了错误，根据校验方程，求得：

$P_{1}^{`}$ =1、 $P_{2}^{`}$ =1、 $P_{3}^{`}$ =0、 $P_{4}^{`}$ =1、 $P_{5}^{`}$ =1；因此求得S1=1、S2=1、S3=1、S4=0、S5=0。

由于S1~S5中有3个不为零，由此可以判断有一个数据位出现了错误；又因为S4~S1的编码为0111，说明第7位海明码出错，也就是D4出错了。

Ending... ...