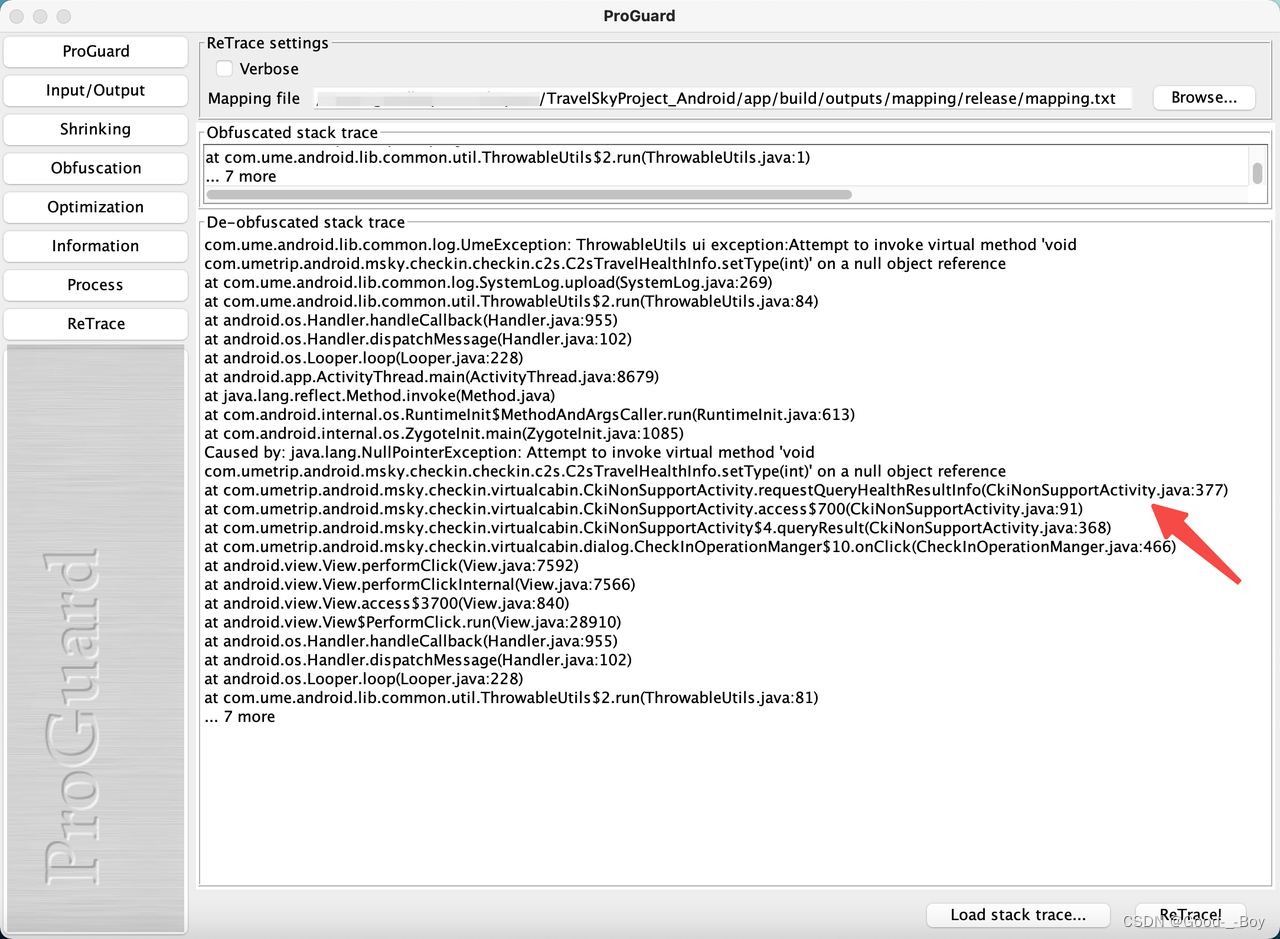
1. 海明码的特点：

 

其中m表示数据位的位数，k表示海明校验码的位数

k位海明校验码一共可以表示种校验信息结果，其中有一种要用来表示没有出错的情况，则其余还剩-1种结果，为了使校验结果可以指出任一位出错的位置，则需要满足以上不等式。

2. 举例说明：

设要传输的数据为101101100

（1）可知m=9，由公式，可知k最小值为4，所以总共要传输的数据位数为9+4=13；

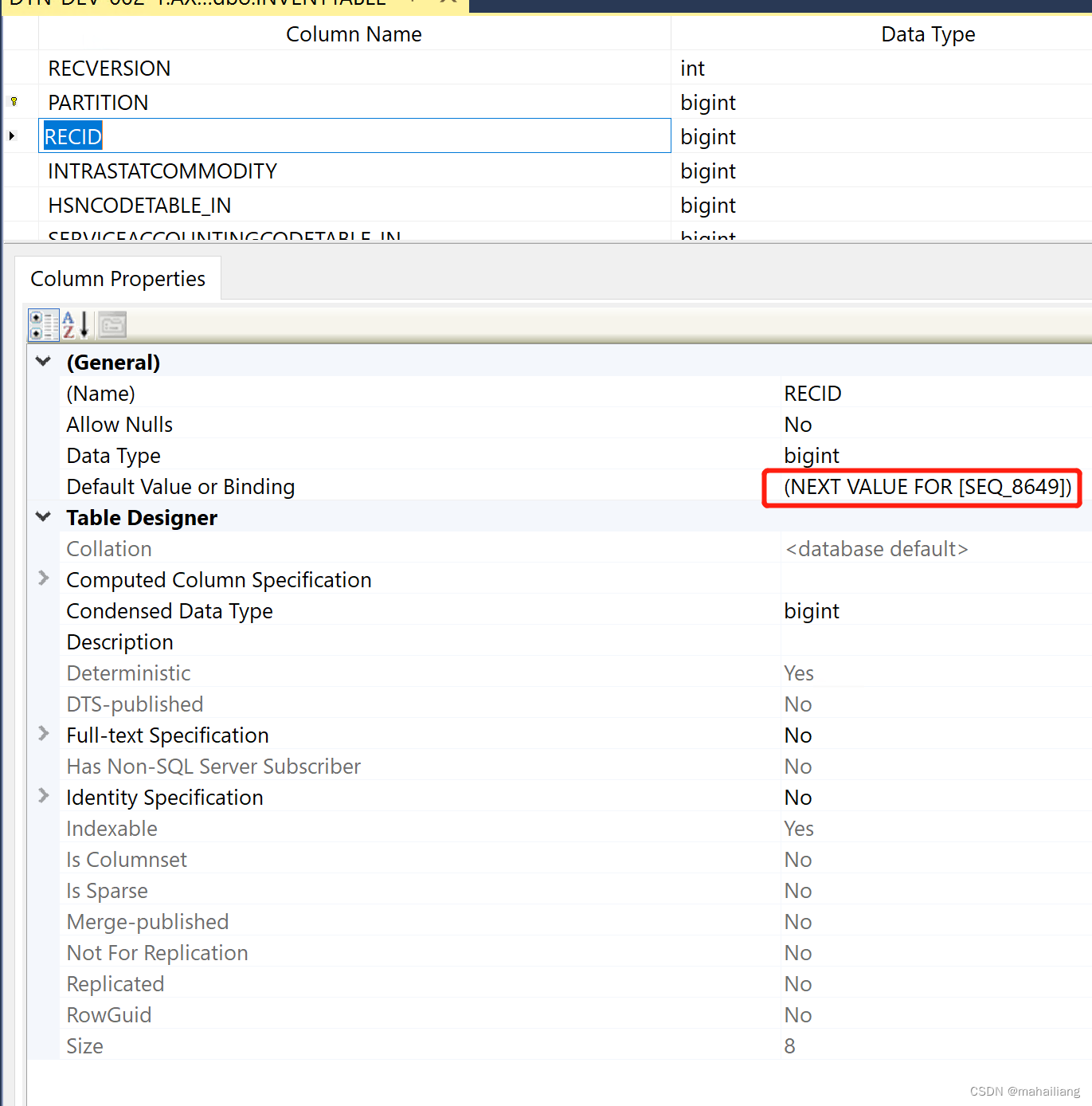
（2）海明校验码放在索引号为的位（n=0,1,2,...,k-1）上，本例中k=4，所以校验位的索引为第1，2，4，8位，于是在下表中把这几位空出来

3.对应表

上表中，先说每一行的内容：从第二行开始，每一行的第一列代表索引号，这个索引号是除去了海明校验位之外的其他所有位。后面几列为该索引号对应的二进制表示，其位数取决于第（1）步计算得出的海明校验码的位数，比如第二行，索引号是3，十进制3对应的二进制就是0011，之所以用4位表示是因为这段信息码需要4个海明校验位。

再看列信息：第一行最右边数字1所对应的列里，出现1的，就表示可以用第H1位完成校验，出现数字0则表示不能用H1位进行校验，因此，由上表可知：

校验位H1负责校验：第3，5，7，9，11，13位（上表黄色高亮显示部分），对应位置上的值进行异或得：1⊕0⊕1⊕0⊕1⊕0=1，由于海明校验做的是偶校验，则H1=1；

校验位H2负责校验：第3，6，7，10，11位（上表蓝色高亮显示部分），对应位置上的值进行异或得：1⊕1⊕1⊕1⊕1=1；
校验位H4负责校验：第5，6，7，12，13位，对应位置上的值进行异或得：0⊕1⊕1⊕0⊕0=0；
校验位H8负责校验：第9，10，11，12，13位，对应位置上的值进行异或得：0⊕1⊕1⊕0⊕0=0。
（4）得到最终要传输的数据串为

 

1. 算校验位

原数据1011, 有4位数据位， 需满足4+r≤2r-1这个公式， 求得r=3，表明有3个检验位，以下用a、b、c、...来代替

得到ab1c011

2. 算校验位值

令发送方和接受方都采用偶检验的方法，也就是保证1的个数为偶数。采用奇检验结果也一样，但收发双方一定要用相同的检验方法。

a b 1 c 0 1 1

第一位检验位a的计算方法：从a开始检验一位，跳过一位，即20位，利用偶检验确定a。

第二位检验位b的计算方法：从b开始检验两位，跳过两位，即21位，利用偶检验确定b。

第三位检验位c的计算方法：从c开始检验四位，跳过四位，即22位，利用偶检验确定c。

---

a b 1 c 0 1 1

a 1 0 1 偶检验确定a=0

---

 a b 1 c 0 1 1

b 1 1 1 偶检验确定b=1

---

 a b 1 c 0 1 1

后面没有了，所以就是c 0 1 偶检验确定c=0

---

 代入abc得海明码0110 011

3. 检验

传输海明码，若在信道上受到干扰，导致一位编码出现异常由0110 011→0111 011

根据确定检验位的值来检验，第n组 检验2n位，跳过2n位，分别把每组的数据异或，得出错位置。这里的异或也就是相当于偶检验的过程，1的个数为偶数G就为0。

---

 0 1 1 1 0 1 1

G1=0⊕1⊕0⊕1=0

---

0 1 1 1 0 1 1

G2=1⊕1⊕1⊕1=0

---

0 1 1 1 0 1 1

G3=1⊕0⊕1⊕1=1

---

由于发送端采用的是偶检验那么G3G2G1=000可说明传送中没有出错，G3G2G1=100转化为十进制说明海明码第4位出错，将第四位纠错后变成0110 011

原文地址：一文看懂海明校验码及其计算方法（详细总结）_被bug卡的寨庭的博客-CSDN博客_海明校验码校验位怎么计算出来的