作为一个新手,写这个强化学习-基础知识专栏是想和大家分享一下自己学习强化学习的学习历程,希望对大家能有所帮助。这个系列后面会不断更新,希望自己在2021年能保证平均每日一更的更新速度,主要是介绍强化学习的基础知识,后面也会更新强化学习的论文阅读专栏。本来是想每一篇多更新一点内容的,后面发现大家上CSDN主要是来提问的,就把很多拆分开来了(而且这样每天任务量也小一点哈哈哈哈偷懒大法)。但是我还是希望知识点能成系统,所以我在目录里面都好按章节系统地写的,而且在github上写成了书籍的形式,如果大家觉得有帮助,希望从头看的话欢迎关注我的github啊,谢谢大家!另外我还会分享深度学习-基础知识专栏以及深度学习-论文阅读专栏,很早以前就和小伙伴们花了很多精力写的,如果有对深度学习感兴趣的小伙伴也欢迎大家关注啊。大家一起互相学习啊!可能会有很多错漏,希望大家批评指正!不要高估一年的努力,也不要低估十年的积累,与君共勉!
Retrace
从本节开始,我们要开始介绍off-policy的策略梯度法,我们首先来介绍一下Retrace,Retrace来自DeepMind在NIPS2016发表的论文Safe and efficient off-policy reinforcement learning。它主要有以下四个特点:
- 低方差。
- 不管有什么样的动作策略进行采样,总是能“安全”地利用这些动作策略采样得到的样本,这里的“安全”我理解是当behavior policy和target policy差很多的时候,依然能保障策略最终的收敛性?
- 对样本的高效使用。
- 第一个不需要GLIE(Greedy in the limit with infinite exploration)假设就能保证收敛的returned-based off-policy control algorithm,其中return-based是之折扣奖励的累积和,它的重点在于一条轨迹或者一段时间,而不是一般的一个点。
然后我们来具体地介绍以下Retrace方法。一般基于 Off-Policy 的价值估计方法主要使用重要性采样的方法实现,我们可以用一个
R \mathrm{R} R 表示这一类计算方法的基本形式:
R Q π ( x , a ) = Q π ( x , a ) + E μ [ ∑ t ⩾ 0 γ t ( ∏ s = 1 t c s ) ( r t + γ Q π ( x t + 1 , ⋅ ) − Q μ ( x t , a t ) ) ] \mathrm{R} Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})=Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})+E_{\mu}\left[\sum_{t \geqslant 0} \gamma^{t}\left(\prod_{s=1}^{t} c_{s}\right)\left(\boldsymbol{r}_{t}+\gamma Q_{\pi}\left(\boldsymbol{x}_{t+1}, \cdot\right)-Q_{\mu}\left(\boldsymbol{x}_{t}, \boldsymbol{a}_{t}\right)\right)\right] RQπ(x,a)=Qπ(x,a)+Eμ[t⩾0∑γt(s=1∏tcs)(rt+γQπ(xt+1,⋅)−Qμ(xt,at))]
其中:
- R被称为operator
- Q ( x , a ) Q(\boldsymbol{x}, \boldsymbol{a}) Q(x,a) 表示值函数估计值
- μ \mu μ 表示参与交互的策略
- π \pi π 表示待学习的策略
- γ \gamma γ 表示回报的打折率
- c s c_{s} cs 是非负的系数,被称为trace of the operator
我们接下来就来讨论当 c s c_{s} cs不同时得到的不同的算法。
-
当target policy π \pi π 和 behaviour policy μ \mu μ完全相同时:
此时 ∏ s = 1 t c s = 1 \prod_{s=1}^{t} c_{s}=1 ∏s=1tcs=1 ,当t=0时,上面的公式就变成了 Actor Critic 中 TD-Error 的计算公式:
R Q π ( x , a ) = r t + γ Q π ( x t + 1 , ⋅ ) \mathrm{R} Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})=\boldsymbol{r}_{t}+\gamma Q_{\pi}\left(\boldsymbol{x}_{t+1}, \cdot\right) RQπ(x,a)=rt+γQπ(xt+1,⋅)
如果时间长度进一步拉长,我们可以得到
R t = 1 Q π ( x , a ) = Q π ( x , a ) + E π [ r t + γ Q π ( x t + 1 ∣ ⋅ ) − Q μ ( x t , a t ) + γ ( r t + 1 + γ Q π ( x t + 2 ∣ ⋅ ) − Q μ ( x t + 1 , a t + 1 ) ) ] = Q π ( x , a ) + E π [ ∑ d = 0 1 γ d ( r t + d + γ Q π ( x t + d + 1 ∣ ⋅ ) − Q μ ( x t + d , a t + d ) ) \begin{aligned} \mathrm{R}_{t=1} Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})=& Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})+E_{\pi}\left[\boldsymbol{r}_{t}+\gamma Q_{\pi}\left(\boldsymbol{x}_{t+1} \mid \cdot\right)-Q_{\mu}\left(\boldsymbol{x}_{t}, \boldsymbol{a}_{t}\right)+\gamma\left(\boldsymbol{r}_{t+1}+\gamma Q_{\pi}\left(\boldsymbol{x}_{t+2} \mid \cdot\right)\right.\right.\\ &\left.\left.-Q_{\mu}\left(\boldsymbol{x}_{t+1}, \boldsymbol{a}_{t+1}\right)\right)\right] \\ =& Q_{\pi}(\boldsymbol{x}, \boldsymbol{a})+E_{\pi}\left[\sum_{d=0}^{1} \gamma^{d}\left(\boldsymbol{r}_{t+d}+\gamma Q_{\pi}\left(\boldsymbol{x}_{t+d+1} \mid \cdot\right)-Q_{\mu}\left(\boldsymbol{x}_{t+d}, \boldsymbol{a}_{t+d}\right)\right)\right. \end{aligned} Rt=1Qπ(x,a)==Qπ(x,a)+Eπ[rt+γQπ(xt+1∣⋅)−Qμ(xt,at)+γ(rt+1+γQπ(xt+2∣⋅)−Qμ(xt+1,at+1))]Qπ(x,a)+Eπ[d=0∑1γd(rt+d+γQπ(xt+d+1∣⋅)−Qμ(xt+d,at+d))
此时的公式形式和 GAE 的计算公式比较接近。 -
当 c s = π ( a s ∣ x s ) / μ ( a s ∣ x s ) c_{s}=\pi\left(a_{s} \mid x_{s}\right) / \mu\left(a_{s} \mid x_{s}\right) cs=π(as∣xs)/μ(as∣xs),上面的式子其实就是重要性采样(Importance Sampling),重要性采样是当target policy π \pi π 和 behaviour policy μ \mu μ 不同时去修正偏差的最简单的一种方式,主要时通过 π \pi π和 μ \mu μ之间的似然率的内积(也可以理解为修正的时sample path的概率)来修正 π \pi π和 μ \mu μ不同时带来的问题。但是重要性采样即使在path有限的情况下也会存在很大的方差,这主要是因为 π ( a 1 ∣ x 1 ) μ ( a 1 ∣ x 1 ) ⋯ π ( a t ∣ x t ) μ ( a t ∣ x t ) \frac{\pi\left(a_{1} \mid x_{1}\right)}{\mu\left(a_{1} \mid x_{1}\right)} \cdots \frac{\pi\left(a_{t} \mid x_{t}\right)}{\mu\left(a_{t} \mid x_{t}\right)} μ(a1∣x1)π(a1∣x1)⋯μ(at∣xt)π(at∣xt)的方差造成的。
-
当 c s = λ c_{s}=\lambda cs=λ时,这是另外一种off-policy correction的方法。由 于 λ \lambda λ 是一个稳定的数值, 所以不会出现IS中的那种连积后有可能会很大的情况。但是一方面这个 数值比较难定, 要有一定的实际经验; 另一方面这种方法并不能保证对任意的 π \pi π 和 μ \mu μ 安全, 这个方法比较适用于 π \pi π 和 μ \mu μ 区别不大的时候。

-
当 c s = λ π ( a s ∣ x s ) c_{s}=\lambda \pi\left(a_{s} \mid x_{s}\right) cs=λπ(as∣xs),这里用上了target policy π ∘ \pi_{\circ} π∘ 保障了算法的安全性, 但是对于两种策略相近时 (称为near on-policy) 的样本利用效率下降了。因为它同样会将一些比较远的轨迹切掉。而在near on-policy的情况下,通常是不希望这样去做的。
-
Retrace ( λ ) : c s = λ min ( 1 , π ( a s ∣ x s ) / μ ( a s ∣ x s ) ) \operatorname{Retrace}(\lambda): c_{s}=\lambda \min \left(1, \pi\left(a_{s} \mid x_{s}\right) / \mu\left(a_{s} \mid x_{s}\right)\right) Retrace(λ):cs=λmin(1,π(as∣xs)/μ(as∣xs)) 。Retrace算是前面提到的算法的优点整合的一个算法,它不仅在 π \pi π 和 μ \mu μ 相差比较大时保障了算法的安全性,而且当 π \pi π 和 μ \mu μ 比较接近时也不会出现切掉较远轨迹,造成效率低的问题。而且由于 c s c_s cs由于最大值是1,所以也不会出现 Π s = 1 t c s \Pi_{s=1}^{t} c_{s} Πs=1tcs 数值很大的情况。
在Retrace的原始论文中,作者对上面提到的几种情况做了总结:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hSP1ntXw-1617629753250)(https://raw.githubusercontent.com/Yunhui1998/markdown_image/main/RL/image-20210329230702993.png)]
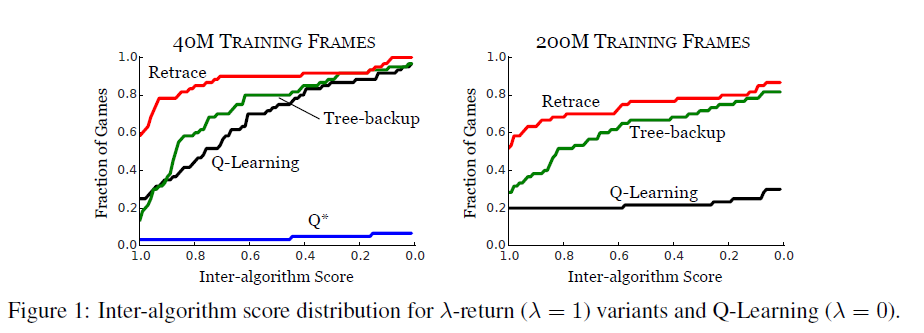
下面是论文中提到的Retrace在60种Artri游戏上的表现,可见Retrace的方法相对于原始的Q-Learning领先非常明显。
上一篇:强化学习的学习之路(五十)2021-02-19 PPO实现策略上的单调提升(Monotonic Improvement with PPO )
下一篇:强化学习的学习之路(五十二)2021-02-21 ACER