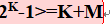
一、检错、纠错和码距
1.1 检错
从接收的报文中,检查出错误。
1.2 纠错
从接收的报文中检查出错误,并改正错误。
一般通过加冗余信息(增大码距)来实现。
1.3 码距
码距是整个编码系统中任意两个码字的最小距离。
也就是说,一个编码 A到和 A 任意不一样的编码 B,最少需要变更的位数。
如果从一个合法编码 A 编导另外一个合法编码 B,最少要变动两位,则码距就是 2。

码距越大,排错能力越好。
1.4 例题
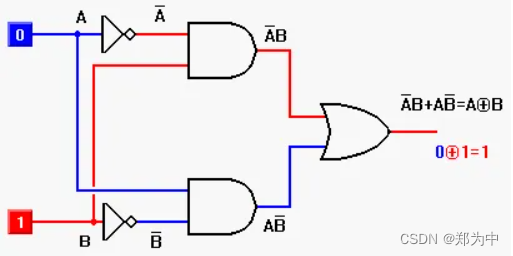
举个例子,若采用 1 位长度的二进制编码,设 A = 0,B = 1,那么 A、B 之间的码距是 1,因为从 0 变到 1 最少需要变 1 位。
如果张三给李四发送了一串编码 0,但李四接收到的编码是 1,那么李四无法识别接收到的编码是否正确,因为张三发送的 0 和李四接收到的 1,都是合法的编码。
若采用 2 位长度的二进制编码,设 A = 00,B = 11,那么 A、B 之间的码距是 2,因为从 00 变到 11 最少需要变 2 位。
如果张三给李四发送了一串编码 00,但李四接收到的编码是 01,那么李四可以确定接受的编码错了,因为只有 00 和 11 是合法的字符,而 01 不合法,但李四无法确定张三发送的到底是 00 还是 11 ,所以只知道错误,但不能纠错。
若采用 3 位长度的二进制编码,设 A = 000,B = 111,那么 A、B 之间的码距是 3,因为从 000 变到 111 最少需要变 3 位。
如果张三给李四发送了一串编码 000,但李四接收到的编码是 001,那么李四可以确定接受的编码错了,因为只有 000 和 111 是合法的字符,而 001 不合法,但李四可以认为接收到的编码就是 000 ,因为李四潜移默化的认为计算机出错概率很小,所以这种情况下知道错误,也能纠错。
二、CRC 循环校验码
CRC 循环校验码是一个只能检错但不能纠错的校验码。
2.1 基本原理
在进行信息编码时,在数据尾部添加一串校验位,让编码后的数据和生成多项式相除且余数为零。
如果接收方校验时,发现余数不为零,则代表传输过程中出现了错误。
CRC 在计算中采用模二除法,即为异或除法。
2.2 例题
原始报文为 11001010101,生成多项式为 X^4+x^3+x+1,对原始报文的编码结果为什么?
首先由生成多项式得出,除数为 11011,其中由于 X 的 2次方没有 1,别的次方位都有 1,所以得出这个结果。
接下来对原始报文的编码进行计算,如下图所示。

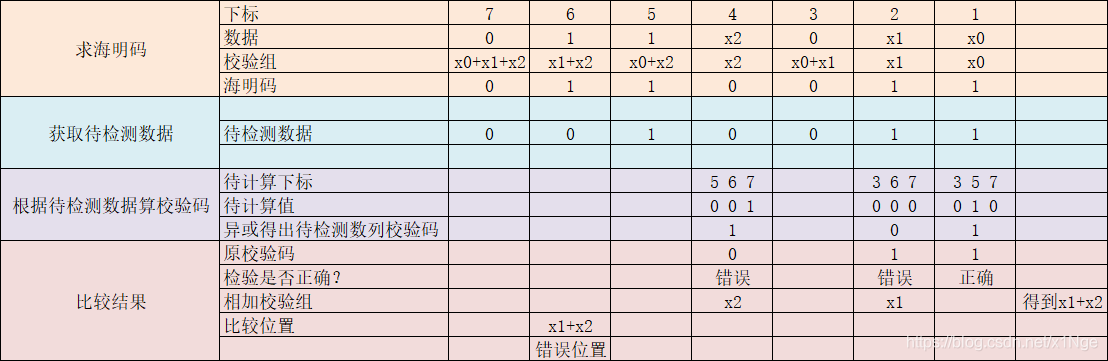
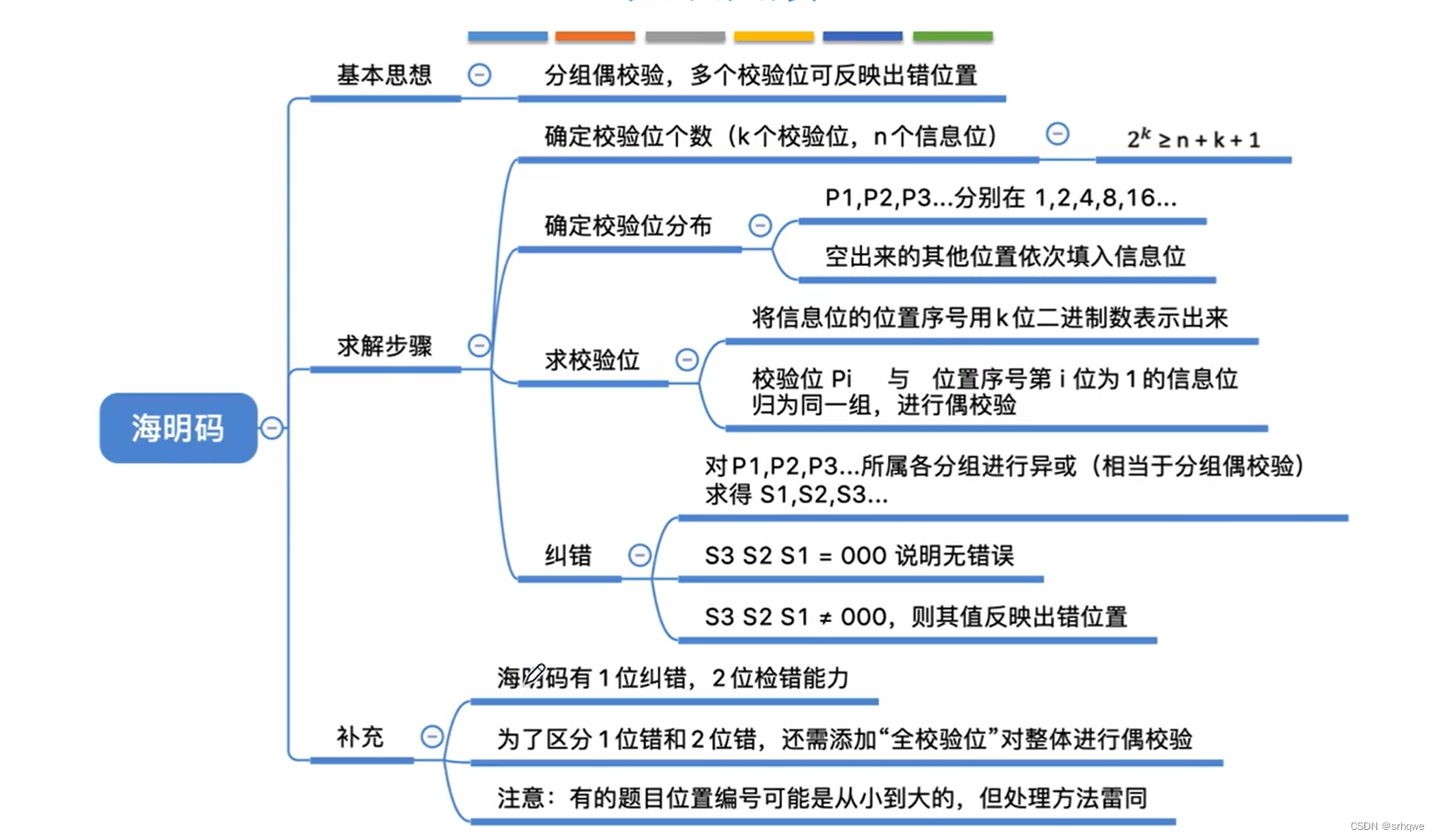
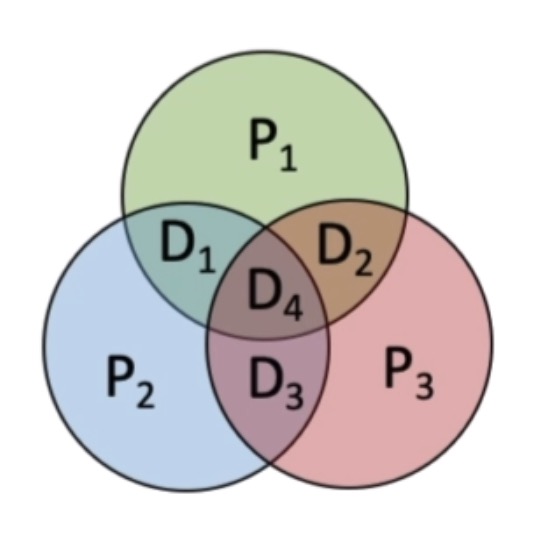
三、海明校验码【重点】
3.1 编码规则
海明校验码的编码规则:
下标为 2 的次方的,为校验位,其余位置为数值位,如下表所示。
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|---|---|---|
| I6 | I5 | I4 | I3 | I2 | I1 | 信息位 | ||||
| r3 | r2 | r1 | r0 | 校验位 |
首先整理下 10 以内的二进制表示。
10 = 2^3 + 2^1
9 = 2^3 + 2^0
8 = 2^3 (校验位 3)
7 = 2^2 + 2^1 + 2^0
6 = 2^2 + 2^1
5 = 2^2 + 2^0
4 = 2^2(校验位 2)
3 = 2^1 + 2^0
2 = 2^1(校验位 1)
1 = 2^0(校验位 0)
整理发现,包含 2 的 3 次方的非校验位数字有 10、9。
包含 2 的 2 次方的非校验位数字有 7、6、5。
包含 2 的 1 次方的非校验位数字有 10、7、6、3。
包含 2 的 0 次方的非校验位数字有 9、7、5、3。
所以 r3 = 表格中下标为 10、9 的数字的异或,即 I6 异或 I5。
所以 r2 = 表格中下标为 7、6、5 的数字的异或,即 I4 异或 I3 异或 I2。
所以 r1 = 表格中下标为 10、7、6、3 的数字的异或,即 I6 异或 I5 异或 I3 异或 I1。
所以 r0 = 表格中下标为 9、7、5、3 的数字的异或,即 I5 异或 I4 异或 I2 异或 I1。
3.2 例题1
若原始报文为 1011,则对原始报文的海明校验编码结果为?
原始报文为 4 位,首先根据公式 4+k+1<2^k ,即 k=3 (校验位为3位),完整码字为7位。
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 信息位 | |||
| r2 | r1 | r0 | 校验位 |
根据二进制拆分可得,包含 2 的 2 次方的非校验位数字有 7、6、5。
所以 R2 = 1 异或 0 异或 1 = 0。
同理,包含 2 的 1 次方的非校验位数字有 7、6、3。
所以 R1 = 1 异或 0 异或 1 = 0。
同理,包含 2 的 0 次方的非校验位数字有 7、5、3。
所以 R1 = 1 异或 1 异或 1 = 1。
所以可得:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 信息位 | |||
| 0 | 0 | 1 | 校验位 |
所以原始报文的海明校验编码结果为 1010101。
3.3 例题2
如果接收方收到的数据为 1011101,即第四位校验位接收错误,如何纠错呢?
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 信息位 | |||
| 1 | 0 | 1 | 校验位 |
分别计算校验位和对应匹配的数据位的异或值即可。
和 R2 匹配的数据位是 7 6 5,所以计算 1 异或 1 异或 0 异或 1 = 1。
和 R1 匹配的数据位是 7 6 3,所以计算 0 异或 1 异或 0 异或 1 = 0。
和 R0 匹配的数据位是 7 5 3,所以计算 1 异或 1 异或 1 异或 1 = 0。
只要有一个校验位不为 0,则说明接收数据错误,如果当且仅当只有一个校验位不为 0,说明只是校验位接收错误,数据位正确,无需更改。
因为 R2 = 1,且 R1 和 R0 都为 0,所以可得 R2 位接收错误,直接取反即可,可得正确数据为 1010101。
3.4 例题 3
如果接收方收到的数据为 1010001,即第五位数据位接收错误,如何纠错呢?
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 信息位 | |||
| 0 | 0 | 1 | 校验位 |
和 R2 匹配的数据位是 7 6 5,所以计算 0 异或 1 异或 0 异或 1 = 0。
和 R1 匹配的数据位是 7 6 3,所以计算 0 异或 1 异或 0 异或 0 = 1。
和 R0 匹配的数据位是 7 5 3,所以计算 1 异或 1 异或 1 异或 0 = 1。
只要有一个校验位不为 0,则说明接收数据错误,如果当且仅当只有一个校验位不为 0,说明只是校验位接收错误,数据位正确,无需更改。
因为 R2 = 0,且 R1 和 R0 都为 1,所以可得上表中下标为 3 的地方接收错误,直接取反即可,可得正确数据为 1010101。
提示:下标 3 的计算方式:2^1 + 2^0 = 3,1 和 0 代表 R1 和 R0。
四、奇偶校验码
奇偶校验码可分为奇校验码和偶校验码。
简单来说在原始报文的尾部(或头部)加一位校验位,奇校验码的校验位等于原始报文中 1 个数对 2 取余,偶校验码 的校验位等于原始报文中 0 个数对 2 取余,如下图所示。

如果原始报文为 011001,那么对于奇校验码,校验位就是 1,因为 原始报文中 1 的个数为 3,3 是奇数,所以校验位是1。
对于偶校验码,校验位是 0,因为 原始报文中 1 的个数为 3,不是偶数,所以校验位是0。
还是举个例子:
| 原始报文 | 奇校验(奇数个 1) | 偶校验(偶数个 1) |
|---|---|---|
| 1111010 | 1111010 1 | 1111010 |
| 1011010 | 1111010 0 | 1111011 |
| 1011000 | 1111010 1 | 1111010 |
| 0011000 | 1111010 0 | 1111011 |
相信聪明的小伙伴已经明白了。
五、总结
本文学习了计算机数据校验的流程,学习了常见的校验方法,比如海明校验码、循环校验码、奇偶校验码,其中海明校验码不但可以检错,还可以纠错,另外两种只能检错不能纠错。