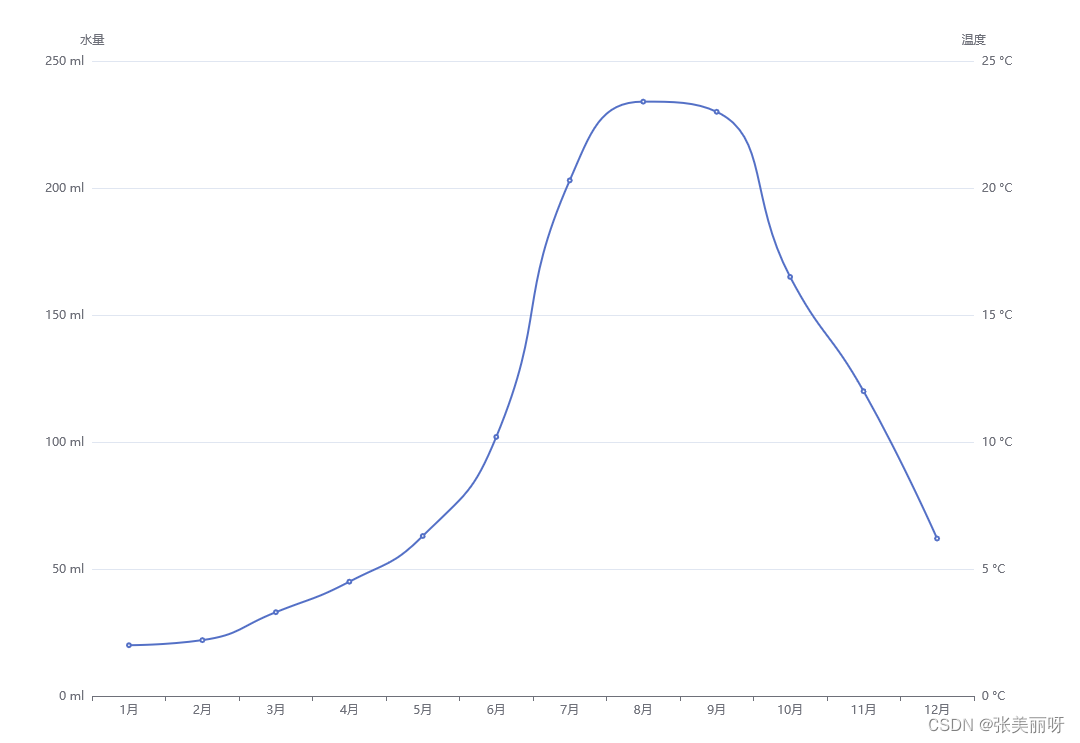
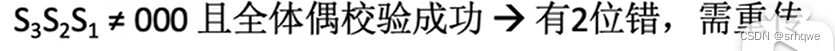计算机底层：海明校验码。

        海明校验码是由奇偶校验码中的偶校验延申出来的：

计算机底层：奇偶校验码_srhqwe的博客-CSDN博客

                了解海明校验码之前需要先了解奇偶校验码。

海明校验码设计思路：

        需要知道：多个校验位就能携带多种状态信息，那么就能够拥有检错和纠错能力。比如：传递1101这串信息，发生了转变，用两种方式进行校验(下面作为初步理解)：

                ①如果使用偶校验码传输时1101变成11101，在传输时，变成10101，发生了改变。但是在一整个二进制中想找到错误，肯定是不能的。

                ②如果使用另一种校验方式1101变成分成2个组A和B组，A是前面两位11，B是后面两位01，此时将通过偶校验码将A中11变成011,B中01变成101，最后变成011101如果在传输时，变成011100，在B组发生了改变。计算机通过异或发现A组没问题，B组中101变成100，那么通过异或后发现有问题，就可以锁定在B组范围出现了问题，缩小了范围，这里使用了两个校验位，那么如果再多一点校验位呢呢？就能实现纠错了。

       

海明校验码的功能：

        ①拥有1bit位的纠错能力，如果数据只有1位出错，海明可以纠正这个错误。

        ②拥有2bit位的查错能力，如果数据2位出错，海明校验码可以发现这个错误，然后叫数据源程序发送数据。

        海明校验码是将信息（二进制序列）进行分组，在将每一组进行添加偶校验位，多个校验位，就可以标记出多个位置。

        既然如此，就需要了解海明校验码是如何进行分组的，又需要用到多少个校验位。

校验位的个数：

        设数据有n位，校验码有x位。则校验码一共有2^x种取值方式。其中需要一种取值方式表示数据正确，剩下2^x-1种取值方式表示有一位数据出错。因为编码后的二进制串有n+x位，因此x应该满足2^x-1 ≥ n+x

        用比较好理解的意思就是：用校验位的一种状态表示一串校验码中一个bit位是否发生了错误。

        因此，2^x种取值方式用来表示n+x位数据的错误状态，那么2^x≥n+x才能够表示，因为还要表示一种正确状态，因此需要2^x≥n+x+1

        这里校验码并不是海明校验码直接判断的依据，因此这里很难理解。但是不用担心，下面会提到这里的，届时你会完全明白这里的意思。

        

校验码个数的对应关系（可以记公式，这张表格也是通过公式推出的）：

        n是数据位数；k是校验位数

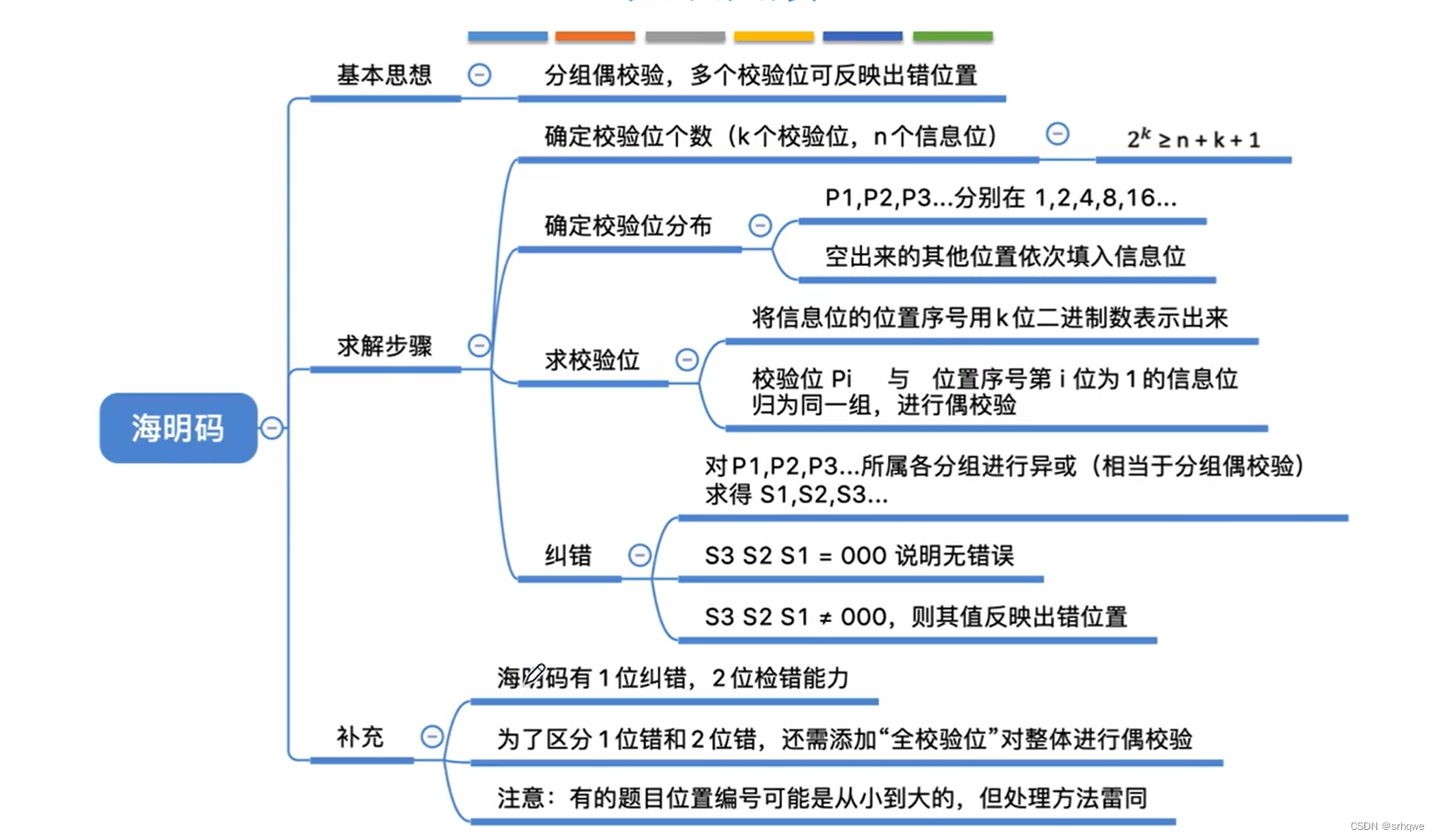
海明码的求解步骤:

实例：

        假设有一串信息：1010

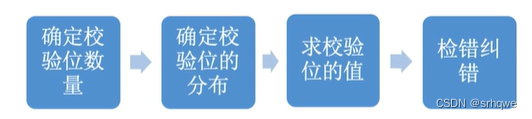
1.确定校验位数量：

        2^k≥n+k+1，其中n是信息位数 n=4

        带入后可以得到k是校验位数 k=3

2.确定校验位的分布

        

        海明校验码规定：将校验位对应放在从H1开始整段海明码第2^i-1的位置上。 

                        

        也就是放在第1，2，4，8，16，32这些位置上(对应了2^x)。

        将Pi放入后，再将其余的信息位Di，从H2开始往后，将空着的位置依次填入Di。

        最后将信息位1010填入：

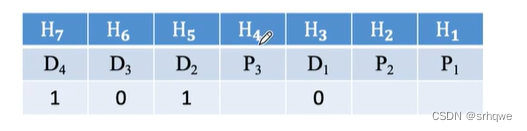
         可以看到图中填入信息的方向，H/D/P下标都是从大到小写入，信息1010是从高位填入低位。其中方向也可以反过来：H1H2H3...反过来后其余的也应该需要反过来。D1D2...P1P2...,信息位方向就是0101。

        校验位有3个，因此可以将信息分成三组，每个分组进行偶校验，就可以实现纠错和检错了。

那么就需要知道海明校验码是如何分组的:

        需要先找到信息位Di的位置：3，5，6，7（对应了H3，H5，H6，H7）

        再将这几个数字转换成二进制：

                

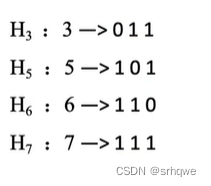
        P3P2P1实际上是一串二进制，所对应的的权值是：P3-2^2,P2-2^1,P1-2^0

        而上图每个H所分解的二进制也有权重，海明校验码就是将与Pi所对应权重的信息位上的信息放入Pi中,形成一个分组：

                

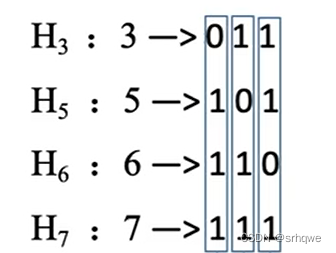
        右边一列表示的权重：2^2

        中间一列表示的权重：2^1

        右边一列表示的权重：2^0

        P1: 1101

        P2: 1011

        p3: 0111

        最后将这些组添加偶校验位（再奇偶校验码中我们知道，将Pi进行异或）,其中是将Hi所对应Di的信息提出来进行异或：

     

       

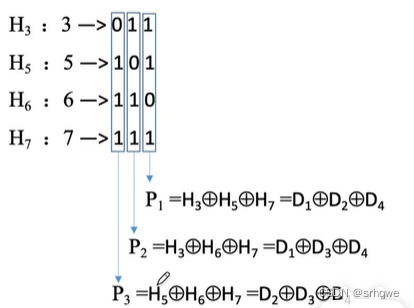
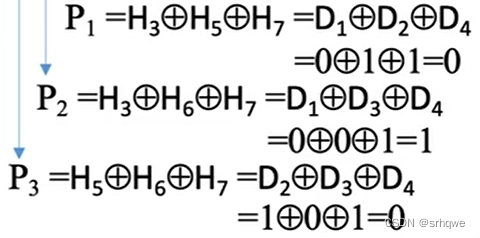
 海明校验码的纠错：

        通过校验位的添加，可以得到三组Si：

        

                 需要注意方向！

        信息位是：1010

        校验位是：P3 P2 P1 == 0 1 0

        对方实际收到的是：校验位和信息为的组合，组合起来的一整串校验码:1010010

                

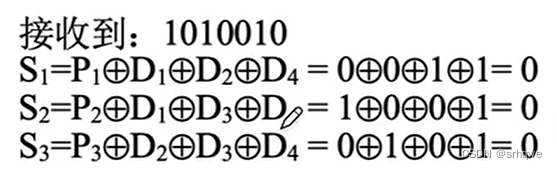
        当接收到1010010时，对方发现1010010分组后的每组异或后都满足偶校验码(异或得0)

                 

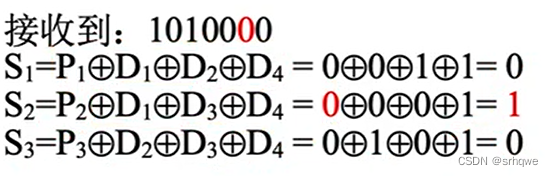
          当接收到1010000时，对方发现1010000分组后的每组异或后S2不满足偶校验码(异或得1)，这就说明出错了。

海明校验码没有两位的纠错能力。但是海明校验码拥有2位的检错能力。

海明校验码纠错：

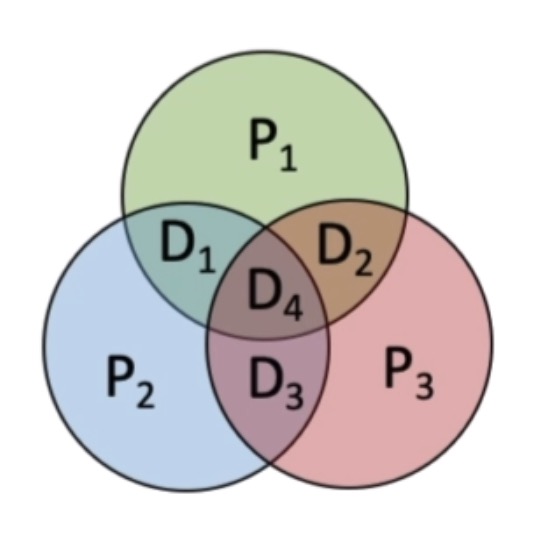
        可以发现Si的三个组是有交集的：

                 

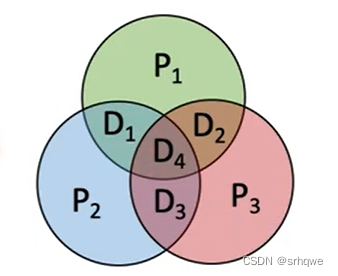
         实际上海明校验码有着一个很神奇的地方：接收方通过对S3S2S1每组的异或可以得到3种不同的数字，如果数据没改变：1010010，那么每组异或后S3=0,S2=0,S1=0,组合后可以得到二进制是000，这是正常状态，如果P2数据改变了，成了：1010001，那么每组异或后S3=0,S2=1,S1=0,组合后可以得到二进制是010，010所对应的十进制就是错误出现的位置：

        因此就能够对应上了上面的校验码设置个数所说的：用校验位的一种状态表示一串校验码中一个bit位是否发生了错误。

         010十进制———2那么就是第二个位置(H2)对应的就是P2，那么错误也就是P2了.

      如果是D4改变了，成了：0010010，那么每组异或后S3=1,S2=1,S1=1,111对应十进制是7,说明D4错误了。

海明校验码的检错：   

        上面是是发生了1个bit位是转变，如果发生了2个bit位的转变呢？：

        如果D1和D2同时发生改变,成了：1000110，会发现S3S2S1都变成111计算机就知道发生了错误，那么111对应的十进制是7，对应的位置H7是D4，显然不是D4发生了改变，但是既然Si是111，那么计算机一定就会将D4改成0，那么这完全就是乱改。为了能够防止这种情况的发生，就需要用到海明校验码的全校验。     

海明校验码的全校验：

        

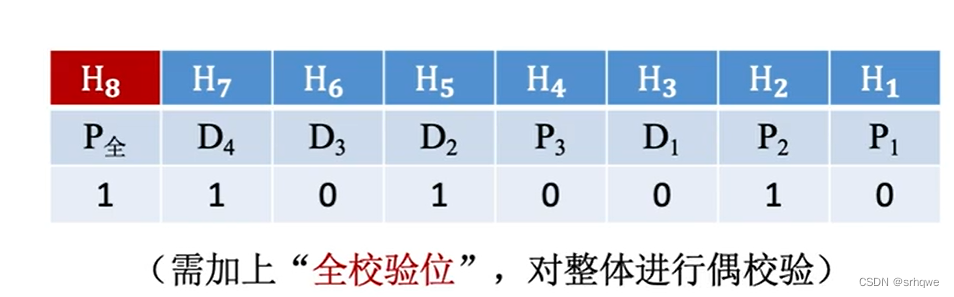
        为什么能够解决呢？

        假设没有发生错误，整串海明校验码11010010符合偶校验码(有偶数个1)，再看Si发现是000，那么海明校验码就知道这串信息没有发生改变：

        

        假设只发生了1bit错误P1发生了错误，那么整串海明校验码11010011不符合偶校验(有奇数个1)，Si是001那么就计算机就知道是001这个位置发生了错误，计算机就会将1改成0：

        

        假设发生了2bit错误P1和P2发生了错误，信息位从变成了11010001 整串海明校验码符合偶校验码(有偶数个1)，但是Si是011,计算机就知道了，这里发生了偶数个bit位的改变。这种改变我解决不了，计算机就会要求对方重传。