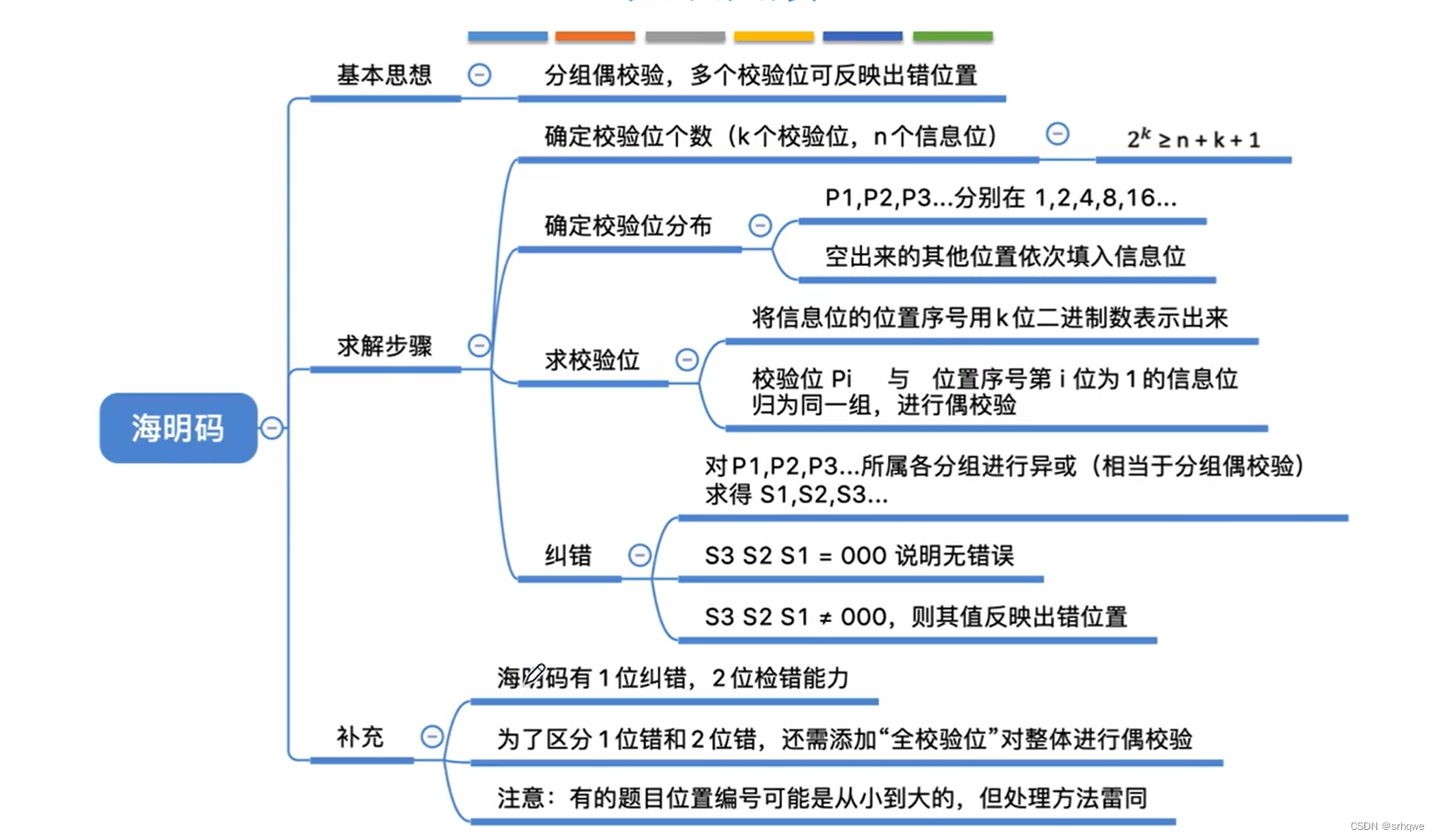
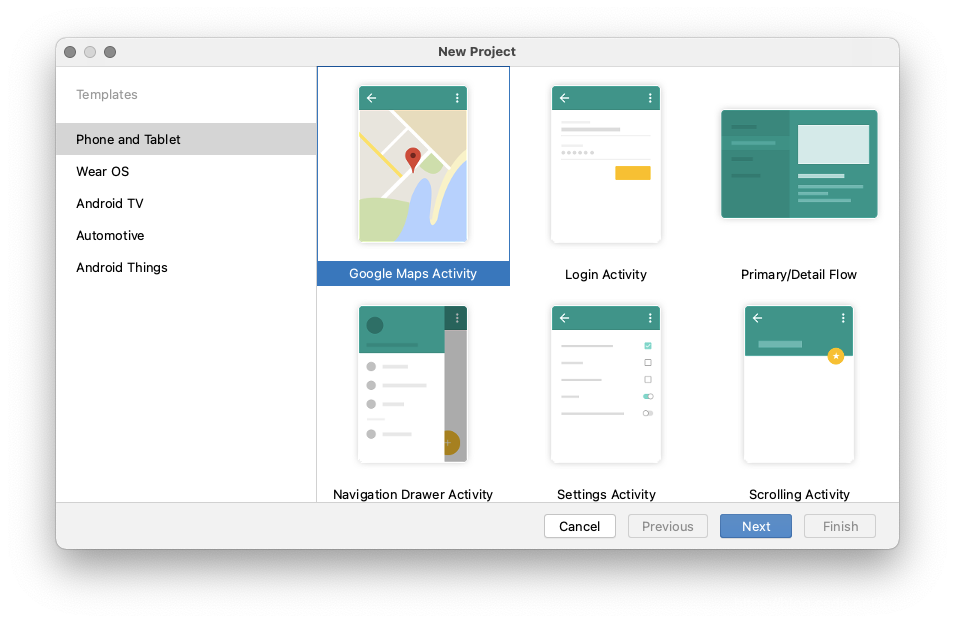
海明校验码原理:在有效的信息为中加入几个校验位形成海明码,使码距[rjazgj1] 比较均匀地拉大,并把海明码的每个二进制位分配到几个奇偶校验组[rjazgj2] 中。当某一位出错后,就会引起有关的几个校验位的值发生变化,这不但可以发现错误,还能指出错误的位置,为自动纠错提供了依据。
公式:![]()
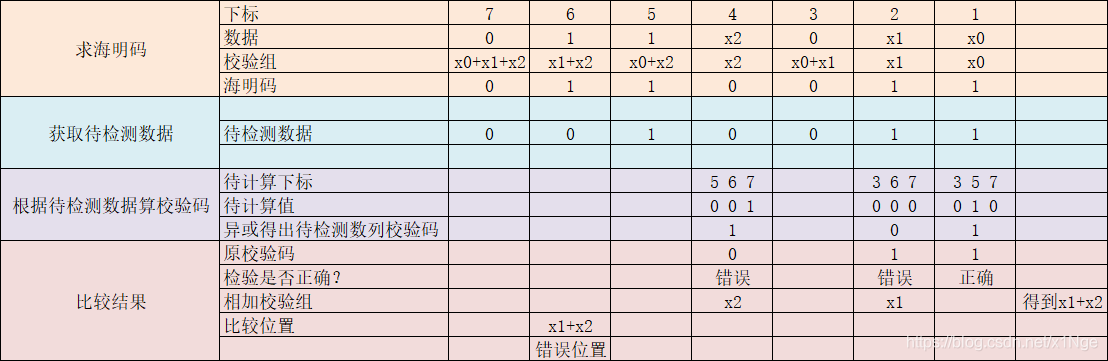
例:设传输的数据为:1010。求海明码。
解:
1) 由公式:![]()
即:2的K次方-1=K+4
得K=3
所以海明码的总位数为4+3=7
| 位(m) | 1(001) | 2(010) | 3(011) | 4(100) | 5(101) | 6(110) | 7(111) |
| 数据 |
|
| 1 |
| 0 | 1 | 0 |
| 校验码 | P1 | P2 |
| P3 |
|
|
|
| 偶海明码 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 奇海明码 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
校验码一般放在2的n次方的位置(n=0 1 2 3 4 …….)
2) 将位用二进制表示出来如表中所示。
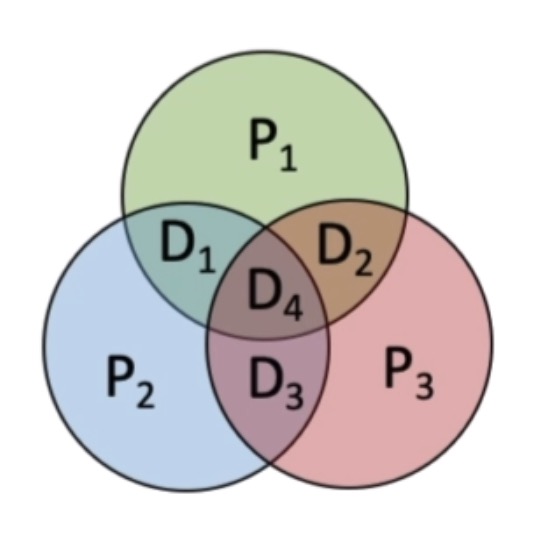
3) 将P与m分组:[rjazgj4]
P1 m3 m5 m7
P2 m3 m6 m7
P3 m5 m6 m7
4)将m3 m5 m7等替换下来即:
P1 1 0 0
P2 1 1 0
P3 0 1 0
5)将P的值分别求出来得出校验码(奇校验:1的个数为奇数。偶校验:1的个数为偶数):
(奇:0偶:1)1 0 0
(奇:1偶:0)1 1 0
(奇:0偶:1)0 1 0
6)海明码检查错误:
发送端:0 1 1 0 0 1 0(奇校验)
接收端:0 1 1 0 0 1 1
6.1)将分组拿来用同时加上错误位置e:
e1 P1 m3 m5 m7
e2 P2 m3 m6 m7
e3 P3 m5 m6 m7
6.2)将分组中的数字替换下来:
e1 0 1 0 1
e2 1 1 1 1
e3 0 0 1 1
6.3)因为是奇校验所以e的值分别为:1 1 1
7)检查错误将e3 e2 e1 写出来为:111转换成10进制为7所以第七位出现错误。
如果 e 的值都是0则没有错误。
注释: