海明校验码的计算及检验
目录
- 海明校验码的计算及检验
- 知识背景
- 计算海明校验码
- 步骤一:计算校验码位数
- 步骤二:确定校验组
- 步骤三:计算校验码的值得出海明校验码
- 利用海明校验码校验数据
- 其他
- 总结
最近和兄弟探讨一个海明校验码的题目,因为学了很久所以有些记不清了,趁这这个机会,复习了一下海明校验码及校验过程,以此为记录。
知识背景
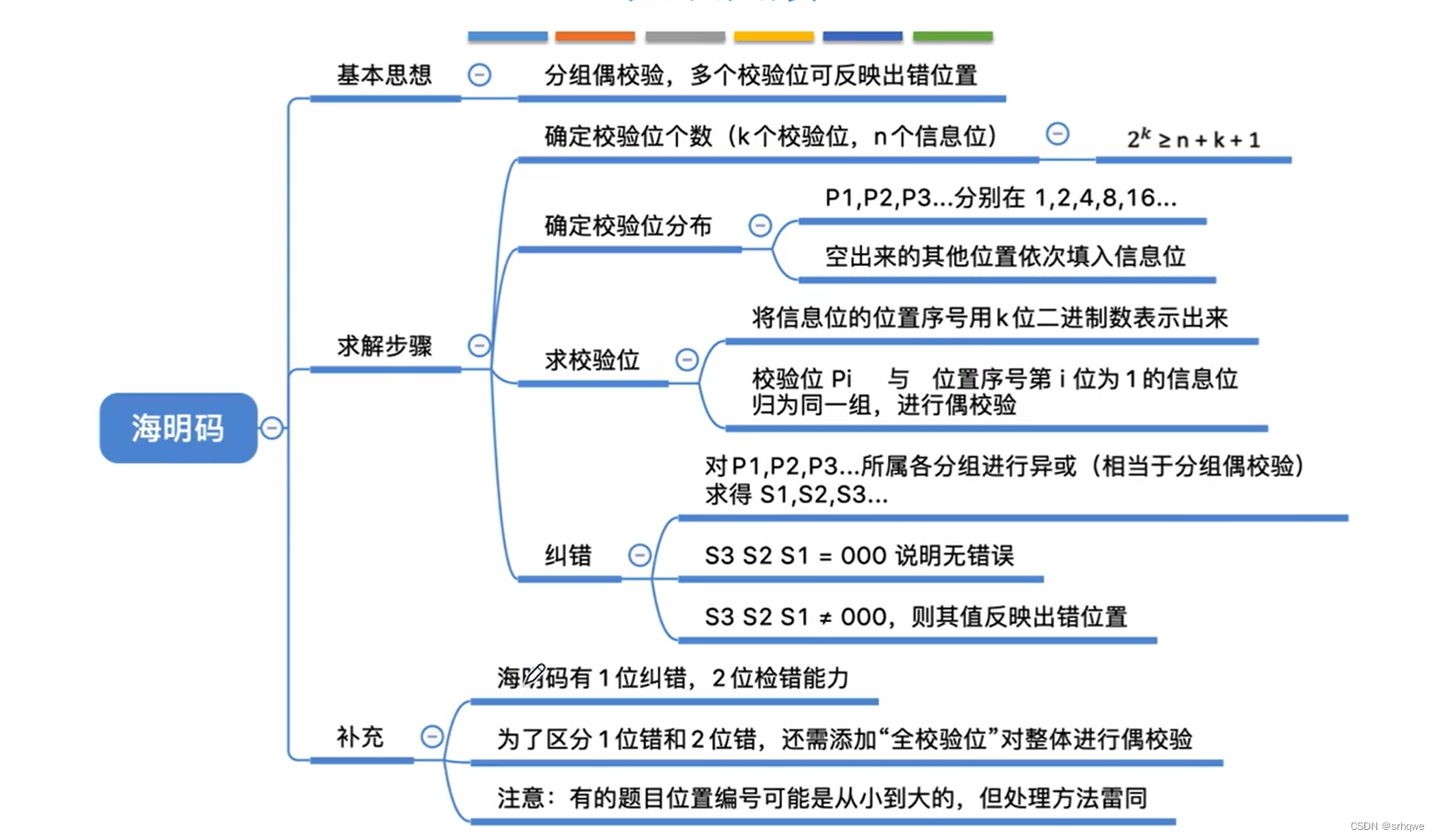
百度百科: “由Richard Hamming于1950年提出、还被广泛采用的一种很有效的校验方法,是只要增加少数几个校验位,就能检测出二位同时出错、亦能检测出一位出错并能自动恢复该出错位的正确值的有效手段,后者被称为自动纠错。”
我们知道,通常情况下使用奇偶校验法可以识别数据是否发生错误,但是并不能知道是哪里的数据发生了问题。有了这个前提,于是我们观察到海明校验码,它增加很少的几个校验位来检测出出错数据的位置,其检测原理概述如下:
百度百科: “它的实现原理,是在k个数据位之外加上r个校验位,从而形成一个k+r位的新的码字,使新的码字的码距比较均匀地拉大。”
现在看来或许还是比较不容易看懂,接下来我用过一个做过的实验题目来分析。
计算海明校验码
首先介绍一下海明校验码公式: 2 k > = n + k + 1 2^k >= n + k + 1 2k>=n+k+1
公式中,k为校验码的位数,n为原数据的位数。
2 k 2^k 2k表示这 k k k位能够表示的状态数,因为每一个校验码都有0或1两种可能,那么和原数据组合产生的状态数量就是 2 k 2^k 2k种,在这么多种可能中有一种状态代表正确校验的情况,而剩下的 2 k − 1 2^k-1 2k−1种状态就用来对应错误校验的情况。
这 2 k − 1 2^k-1 2k−1种情况最起码要比总位数(原数据位数+校验码位数)多,所以就得到 2 k − 1 > = n + k 2^k-1>=n+k 2k−1>=n+k
通过这个公式,我们就可以计算出一个已知原始数据所需要的最小校验位数。下面举一个我做过的一个实验题目作为例子:
| 下标 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| 数据 | 0 | 1 | 1 | 0 |
步骤一:计算校验码位数
这一原始数据 0110 0110 0110, n = 4 n = 4 n=4,根据海明校验码公式可以得到需要添加的校验码位数 k = 3 k=3 k=3
有话说: 校验码放置的位置应为2的整数次幂,即 P i = 2 i P_{i}=2^i Pi=2i.
于是我们得到了这样一个待计算的海明码:
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 数据 | 0 | 1 | 1 | P 2 P_{2} P2 | 0 | P 1 P_{1} P1 | P 0 P_{0} P0 |
其中, P 0 P_{0} P0、 P 1 P_{1} P1、 P 2 P_{2} P2为三个我们添加的校验码
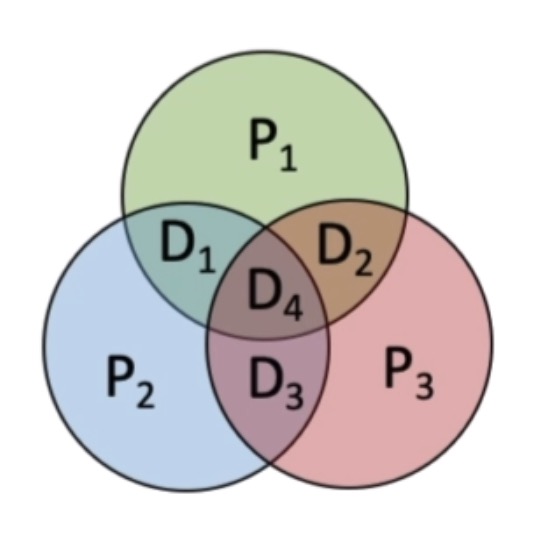
步骤二:确定校验组
接下来我们为每一个数据添加校验组,校验组是什么意思呢,就是这一下标对应的数据可以由一个校验组来唯一对应检验。通俗地讲,做法就是将每一个数据位的下标分解成校验码所在下标的和,(校验位不分解),拿我们的例子来看看:
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 下标分解 | 1+2+4 | 2+4 | 1+4 | 4 | 1+2 | 2 | 1 |
| 数据 | 0 | 1 | 1 | P 2 P_{2} P2 | 0 | P 1 P_{1} P1 | P 0 P_{0} P0 |
| 校验组 | P 0 P_{0} P0、 P 1 P_{1} P1、 P 2 P_{2} P2 | P 1 P_{1} P1、 P 2 P_{2} P2 | P 0 P_{0} P0、 P 2 P_{2} P2 | P 2 P_{2} P2 | P 0 P_{0} P0、 P 1 P_{1} P1 | P 1 P_{1} P1 | P 0 P_{0} P0 |
有话说: 例如下标5还可以分解成2+3那为什么不选2+3呢?这是因为下标3是数据位而不是校验位,所以这里我们选的是1+4的分解。
这样一来,每一个数据都可以由唯一确定的校验组来校验
步骤三:计算校验码的值得出海明校验码
计算海明校验码的最后一个步骤就是得出 P 0 P_{0} P0、 P 1 P_{1} P1、 P 2 P_{2} P2的具体值,其做法为:
计算 P i P_{i} Pi的值,就在校验组中将与 P i P_{i} Pi有关的那几组数据做 异或(相同为0,不同为1) 运算
拿我们的例子来看看:
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 数据 | 0 | 1 | 1 | P 2 P_{2} P2 | 0 | P 1 P_{1} P1 | P 0 P_{0} P0 |
| 校验组 | P 0 P_{0} P0、 P 1 P_{1} P1、 P 2 P_{2} P2 | P 1 P_{1} P1、 P 2 P_{2} P2 | P 0 P_{0} P0、 P 2 P_{2} P2 | P 2 P_{2} P2 | P 0 P_{0} P0、 P 1 P_{1} P1 | P 1 P_{1} P1 | P 0 P_{0} P0 |
| 有关下标 | 5 6 7 | 3 6 7 | 3 5 7 | ||||
| 运算 | 1 ⊕ 1 ⊕ 0 1\oplus1\oplus0 1⊕1⊕0 | 0 ⊕ 1 ⊕ 0 0\oplus1\oplus0 0⊕1⊕0 | 0 ⊕ 1 ⊕ 0 0\oplus1\oplus0 0⊕1⊕0 | ||||
| 结果 | 0 | 1 | 1 |
计算结束后,和原来的数据组合我们就得到了海明校验码:
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 数据 | 0 | 1 | 1 | P 2 P_{2} P2 | 0 | P 1 P_{1} P1 | P 0 P_{0} P0 |
| 海明校验码 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
利用海明校验码校验数据
接下来我们利用海明校验码来校验数据:
例如我们有一个待检测的数据:
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 数据 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
由上文所讲,校验码的值是由与之相关的数据异或得到,例如: P 0 = 0 ⊕ 1 ⊕ 0 = 1 P_{0}=0\oplus1\oplus0=1 P0=0⊕1⊕0=1,所以如果这个校验码的值没有改变,即 P 0 ′ = P 0 P'_{0}=P_{0} P0′=P0,那么我们可以得到的就是 P 0 ′ ⊕ P 0 = 0 P'_{0}\oplus P_{0}=0 P0′⊕P0=0,反之,若 P 0 ′ ⊕ P 0 = 1 P'_{0}\oplus P_{0}=1 P0′⊕P0=1我们就可以判定该校验位所能够影响的几个位置存在错误。其中 P 0 ′ P'_{0} P0′为待检测数据按上述同样方法计算的校验码的值。以上述待检测数据为例:
P 0 ′ ⊕ P 0 = 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0 P'_{0}\oplus P_{0}=0\oplus1\oplus0\oplus1=0 P0′⊕P0=0⊕1⊕0⊕1=0 正确
P 1 ′ ⊕ P 1 = 0 ⊕ 0 ⊕ 0 ⊕ 1 = 1 P'_{1}\oplus P_{1}=0\oplus0\oplus0\oplus1=1 P1′⊕P1=0⊕0⊕0⊕1=1 该校验位能影响的位置存在错误
P 2 ′ ⊕ P 2 = 1 ⊕ 0 ⊕ 0 ⊕ 0 = 1 P'_{2}\oplus P_{2}=1\oplus0\oplus0\oplus0=1 P2′⊕P2=1⊕0⊕0⊕0=1 该校验位能影响的位置存在错误
| 下标 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 数据 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 校验组 | P 0 ′ P'_{0} P0′、 P 1 ′ P'_{1} P1′、 P 2 ′ P'_{2} P2′ | P 1 ′ P'_{1} P1′、 P 2 ′ P'_{2} P2′ | P 0 ′ P'_{0} P0′、 P 2 ′ P'_{2} P2′ | P 2 ′ P'_{2} P2′ | P 0 ′ P'_{0} P0′、 P 1 ′ P'_{1} P1′ | P 1 ′ P'_{1} P1′ | P 0 ′ P'_{0} P0′ |
| 有关下标 | 5 6 7 | 3 6 7 | 3 5 7 | ||||
| P i ′ P'_{i} Pi′ | 1 ⊕ 0 ⊕ 0 = 1 1\oplus0\oplus0=1 1⊕0⊕0=1 | 0 ⊕ 0 ⊕ 0 = 0 0\oplus0\oplus0=0 0⊕0⊕0=0 | 0 ⊕ 1 ⊕ 0 = 1 0\oplus1\oplus0=1 0⊕1⊕0=1 | ||||
| P i P_{i} Pi | 0 | 1 | 1 | ||||
| P i ′ ⊕ P i P'_{i}\oplus P_{i} Pi′⊕Pi | 1 | 1 | 0 |
由此我们组合可能出现错误位置的校验码 P 1 ′ + P 2 ′ P'_{1}+P'_{2} P1′+P2′对应下标为6的数据,将它取反便可更正。
其他
其实这里也可以这样理解,相当于给这个新的数据求新的校验值和原来的比对:
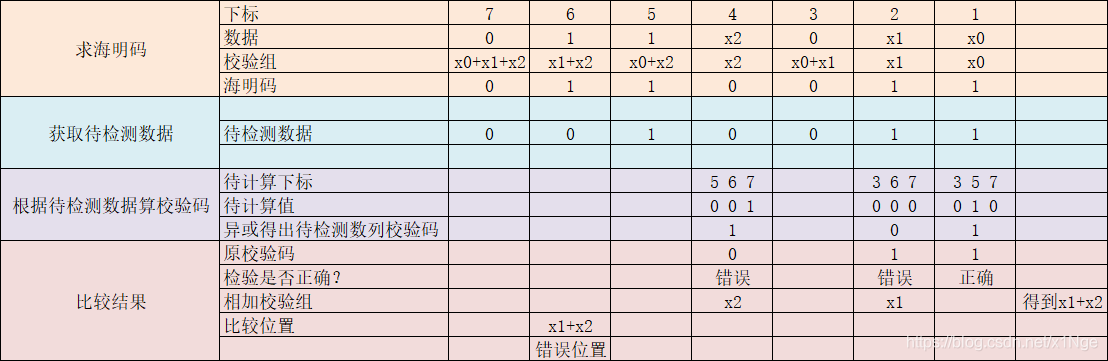
总结
- 同步更新至CSDN,仅作实验记录之用。
- 水平有限,文章有需要改正之处还望指出。