本章主要讲解隐函数求导和相关变化率，大家理解什么叫隐函数及其如何求导
隐函数求导
相关变化率

隐函数求导

首先我们来理清什么叫隐函数，讲解隐函数之前我们来讲显函数，因为隐函数是相对显函数而言的

1. $y=f(x)$像这种函数中，明显的用一个变量$x$来表示另一个变量$y$。例如：$y=x^2$
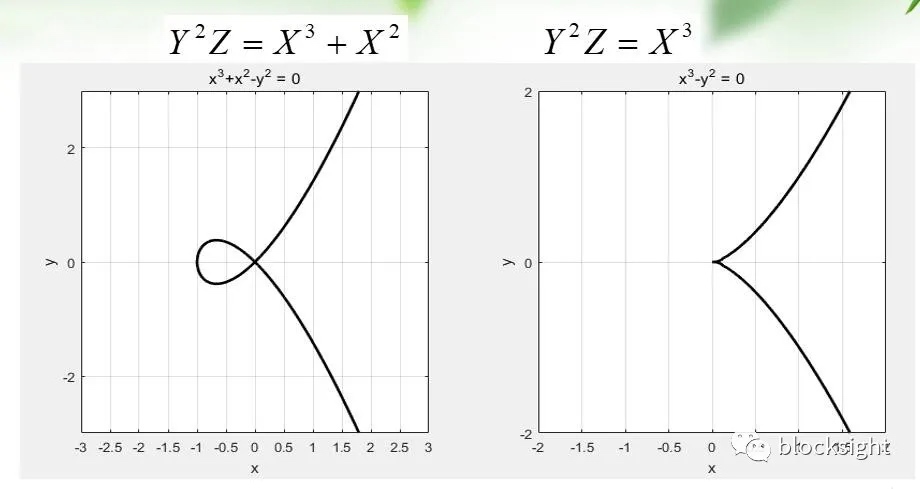
2. $F(x,y)=0$像这种函数中（确切的说是一个方程），像这种函数中并没有表明变量$x$和$y$的关系，但是他们之间又存在一定的关系。例如：$x^2+y^2=4$。这个方程表示的是一个圆心在原点上，半径为2的圆。表达式中并看不出$x$和$y$存在什么关系。这叫隐函数

【例】求解函数$x^2+y^2=4$的导数
【解】 对函数左右两边的$x$求导，那么$y$怎么办呢？我们可以把$y$看做$x$的函数$y=y(x)$，然后我们在对y进行求导
1、对$x$求导
$$\frac{d}{dx}(x^2)=2x$$
2、对$y$求导，首先把$y$当做$x$的函数，即：$y=y(x)$。可以这么理解$y$和$x$存在一定的关系，但是到底是什么关系现在我们也不确定，反正就是有关系。
$$\frac{d}{dx}(y^2)=2y\frac{dy}{dx}$$
这里首先是对$y^2$求导得$2y$，然后再乘上$y$关于$x$的求导$\frac{dy}{dx}$，至于他们的关系是未知的，是需要我们去求解的
3、对常数进行求导$$\frac{d}{dx}4=0$$
4、整合公式$$\frac{d}{dx}(x^2)+\frac{d}{dx}(y^2)=2x+2y\frac{dy}{dx}$$
5、整理得
$$\frac{dy}{dx}=-\frac{2x}{2y}=-\frac{x}{y}$$
这个公式说的是，圆上的点$(x,y)$处的切线的斜率为$-\frac{x}{y}$；

如果先给出圆上的点$(1,\sqrt{3})$；求结果该点处切线的方程呢？

1、首先把该点带入方程，验证是否在圆上$$1^2+(\sqrt{3}{)}^2=1+3=4$$
2、求该点切线斜率$$\frac{dy}{dx}=-\frac{x}{y}=-\frac{1}{\sqrt{3}}$$
3、根据点斜式求出方程$$y-\sqrt{3}=-\frac{1}{\sqrt{3}}(x-1)$$

相关变化率

设想有两个量存在关系，如这两个量中一个发生变化另外一个也会发生相应的变化；如果我们在进一步的研究，如果其中一个量变化有多快，那么另外一个量的变化又有多快呢？这是我们所说的相关变化率的意思；变化率是一个量随时间改变的速率。所以变化率是和时间相关的。
如果你想知道某物随时间的变化有多快，只要简单的对其关于时间求导即可。
如：量Q的变化率是Q关于时间的导数，那么Q的变化率是$\frac{dQ}{dt}$

解题技巧

我们只要对方程两边进行关于时间做隐函数求导，然后解出这个方程即可

【例一】设想用打气筒给一个气球打气，空气以常数变化率$12\pi$立方英寸每秒进入气球，当气球的半径达到2英寸时，气球的半径的变化率是多少呢？当气球的体积达到$36\pi$立方英寸时，气球的半径的变化率又是多少？
【分析】大家试想一下，以$12\pi$立方英寸每秒的速率充气，那么气球的体积越大，球的半径变化就越慢，首先我们写出球体的计算公式$$V=\frac{4}{3}\pi r^3$$
首先我们对方程两边关于时间隐函数求导$$\frac{d}{dt}(V)=\frac{d}{dt}(\frac{4}{3}\pi r^3)$$
方程右边采用乘法求导法则，因为$\frac{4}{3}$和$\pi$都是自然数，导数为0，最后只剩$r^3$。因为$$\frac{d}{dt}(r^3)$$是$r$关于时间$t$求导的隐函数，所以先对$r^3$求导得$3r^2$，然后乘以$\frac{dr}{dt}$得$3r^2\frac{dr}{dt}$；所以右边最终得到$r$关于时间求导的表达式$$4\pi r^2\frac{dr}{dt}$$
方程左边正好是体积关于时间的变换率，体积的变化率是$12\pi$立方英寸/秒。$$\frac{dV}{dt}=12\pi$$左边是体积$V$关于时间$td$的变化率，右边是半径$r$关于时间的变化率$$12\pi =4\pi r^2\frac{dr}{dt}$$化简后$$\frac{dr}{dt}=\frac{3}{r^2}$$从结果可以看出半径的变化率本身就依赖半径，大家可是试想一下，我们在吹气球的时候，当求被吹越大的时候发现气球变化越来越小。
现在我们就可以正式求出问题中的答案
1、当气球的半径达到2英寸的时候，气球的半径变化率是多少？
$$\frac{dr}{dt}=\frac{3}{r^2}=\frac{3}{2^2}=\frac{3}{4}$$
2、当体积为$36\pi$立方英寸时，气球的半径变化率又是多少？首先我得计算出半径$r$才能计算出半径的变化率$$36\pi =\frac{4}{3}\pi r^3$$最终计算出$r=3$代入公式$$\frac{dr}{dt}=\frac{3}{r^2}$$得$$\frac{dr}{dt}=\frac{1}{3}$$因此，当体积达到$36\pi$立方英寸时，半径的变化率是$\frac{1}{3}$

【例二】如下图所示，有两辆汽车A和B，汽车A在一条路上经直向北行驶远离你家，而汽车B在另外路上经直向西行驶接近你家，汽车A以55英里/小时的速度行驶，而汽车B以45英里/小时的速度行驶，当A到达你家北面21英里，而B到达你家东面28英里时，两辆汽车的距离的变化率是多少呢？
【例二】题目中涉及到三个变化率，A汽车距离你家的变化率（55英里/小时），B汽车距离你家的变化率（45英里/每小时），A、B两辆车的距离变化率（未知）；根据直角三角形的公式$$a^2+b^2=c^2$$直接对等号左右两边关于时间$t$做隐函数求导得$$\frac{d}{dt}(a^2)+\frac{d}{dt}(b^2)=\frac{d}{dt}(c^2)$$因为这三个（a、b、c）变量都是关于时间的隐函数，首先对每个变量都分别求导，然后再乘以$\frac{d}{dt}$(变量关于时间求导)；例如：$a^2$求导得$2a$，然后再a关于时间求导乘以$\frac{da}{dt}$$$2a\frac{da}{dt}+2b\frac{db}{dt}=2c\frac{dc}{dt}$$化简得$$a\frac{da}{dt}+b\frac{db}{dt}=c\frac{dc}{dt}$$
把a、b的变化率和值带入公式
$$21\times 55+28\times (-45)=c\frac{dc}{dt}$$简化得$$\frac{dc}{dt}=-\frac{105}{c}$$这里特别注意：因为B车离家原来越近，所以是负方向；最后我们计算c的值$$a^2+b^2=c^2=>55^2+45^2=c^2$$最后计算出$c{=}_{+}^{-}\text{35}$；因为c是正数得$c=35$；带入计算$$\frac{dc}{dt}=-\frac{105}{35}$$$$\frac{dc}{dt}=-3$$
因此：当A到达你家北面21英里，而B到达你家东面28英里时，两辆汽车的距离的变化率是-3
是负数说明在该时刻两辆车的距离以3英里/每小时的变化率在减少