为什么学高数?
锻炼自己的思维,以防老年痴呆。
如何服用高等数学?(学习方法)
做题不盲目做,一点点增加难度,难题一定要自己做出来不急于求成知道答案,过程对你很重要。
课程目标:
1、微积分/代数/概率统计;
2、基础课程/提高课程;
3、保持适当的题量;
4、以逻辑符号来叙述;
目录
一、函数
1、实数
集合的分类
2、领域
3、函数的概念
函数相等及其判定
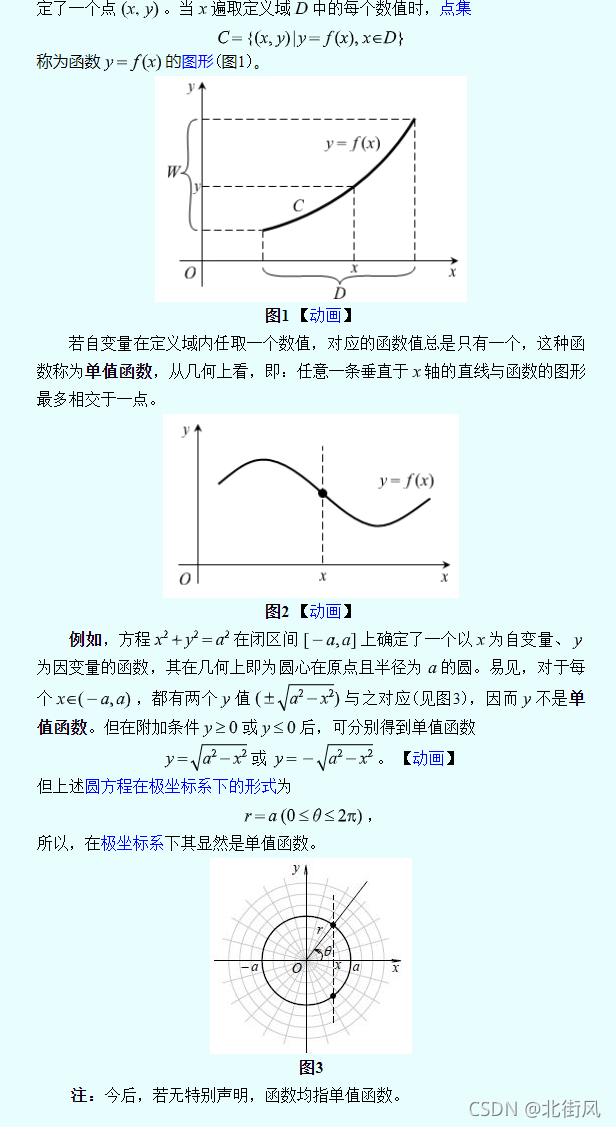
4、函数的图形
5、分段函数举例
6、函数的有界性
7、函数的单调性
二、映射与集合
一、函数
学高数之前先衔接一下高中的函数。
1、实数

任意两个有理数之间都包含着无穷多个有理数,此即所谓的有理数集的稠密性;
有理数与无理数的全体称为实数,这样就把有理数集扩展到了实数集。
集合的分类
(1) 集合依据其所含元素的个数可分为有限集和无限集。含有有限个元素的集合称为有限集;含有无限个元素的集合称为无限集。
(2) 集合按元素的属性可分为数集、点集与其他集合。
自然数集记为N,整数集记为Z,有理数集记为Q,实数集记为R,这些数集间的关系如下:
![]()
区间是数学中常用的实数集。我们在高中阶段已学习过区间的概念,为应用方便,再做如下总结。
区间分为有限区间和无限区间两类。
(1)有限区间

(2)无限区间

2、领域

3、函数的概念
函数是描述变量间相互依赖关系的一种数学模型。
映射与一一映射(对应)
1、映射的定义
设是两个非空集合,若对于集合中的任意一个元素,按照某一个确定的对应关系,在集合中都存在唯一确定的元素与之对应,则称对应为从集合到集合的一个映射。
2、一一映射(对应)的定义
设是两个非空集合,是集合到集合的映射,若在这个映射下,集合中的不同元素在集合中有不同的像,而且中每一个元素都有原象,则这个映射称为从到的一一映射,也称为与之间的一一对应。注:映射与函数的联系的区别
函数是定义在两个数集上的,但映射定义在一般的集合(如数集、点集以及由图形等组成的集合)上,故函数一定是映射,但映射不一定是函数。

常量:在某一变化过程中,数值始终不变的量;
变量:在某一变化过程中,数值发生变化的量;
该函数图像为

扩展
学过的常用函数的定义域:
(1) 比例函数、一次函数与二次函数的定义域为实数集;
(2) 反比例函数的定义域是使分母不等于零的实数的全体,即
;
进一步,如果是分式函数,则其定义域为使其分母不为零的实数的全体。
(3) 二次根式函数的定义域:
函数相等及其判定

注1:函数的定义域与对应法则称为函数的两个要素。两函数相等的充要条件是其定义域与对应法则相同,而函数的自变量用什么字母表示无关,此即函数自变量表示的无关性。
充要条件:
充分条件与必要条件
在高中阶段,我们学习过有关命题条件与结论的充分条件与必要条件、四种条件的判断
等。为应用方便,下面再简要总结如下。1、从逻辑推理关系看,条件与的关系分为四类:
(1) 充分条件:若,则称是的充分条件;(2) 必要条件:若,则称是的必要条件。
其逆否命题即为:不成立则必定不成立。也就是常说的“有它不一定行,而没它肯定不行”。
(3) 充分必要条件:若且,则称是的充分必要条件(或的充分必要条件是),简称充要条件。同时,也称也是的充要条件。注:有些叙述中的“当且仅当”即为“充要条件”。
(4) 既不充分也不必要条件:若且,则既不是的充分条件也不是的必要条件。2、四种条件的判断方法
(1) 定义法
a. 分清条件和结论:分清哪个是条件,哪个是结论;
b. 找推式:判断“”及“”的真假;
c. 下结论:根据推式及定义下结论。
(2) 等价法
将命题转化为另一个与其等价的以便于判断真假的命题,利用原命题与其逆否命题等价,逆命题与否命题等价来判断。
注:命题条件与结论的充分条件与必要条件,还可从集合的角度来理解与判断。
例题:

4、函数的图形
函数有三种表示方法:解析法、列表法与图象法。
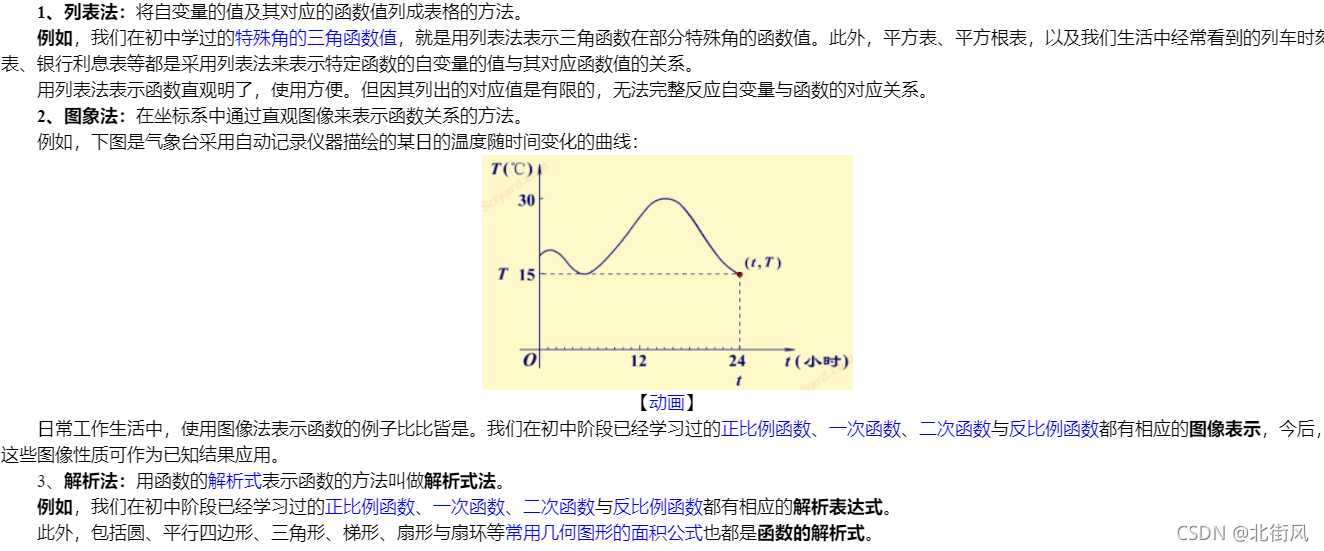
根据函数的解析表达式的形式不同,函数也可分为显函数、隐函数和分段函数三种:

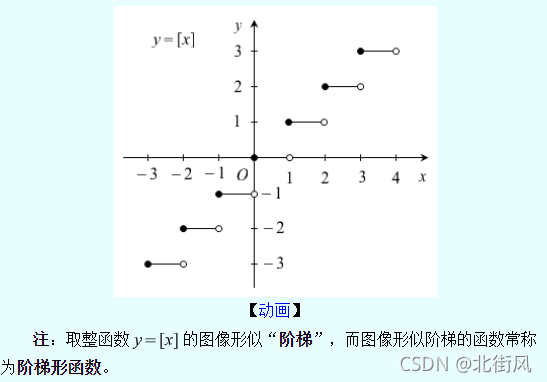
5、分段函数举例
绝对值的定义与几何意义
实数的运算法则与运算规律
绝对值三角不等式的基本(推广、复数、向量)形式
几个重要常用的缩放不等式
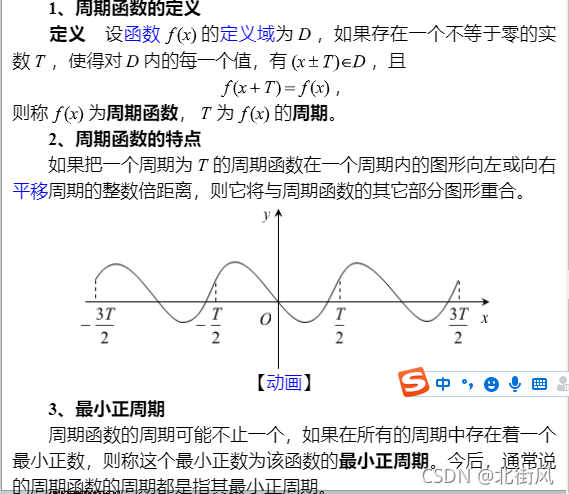
周期函数的定义,周期与最小正周期
函数图像的平移、伸缩、对称与翻折变换
6、函数的有界性
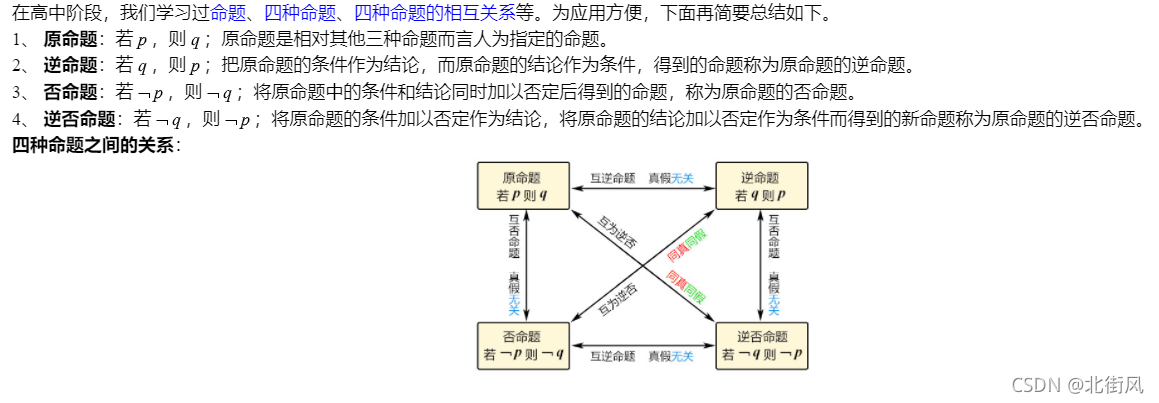
四种命题及其关系
充分条件与必要条件(从逻辑推理关系与集合角度看)
7、函数的单调性
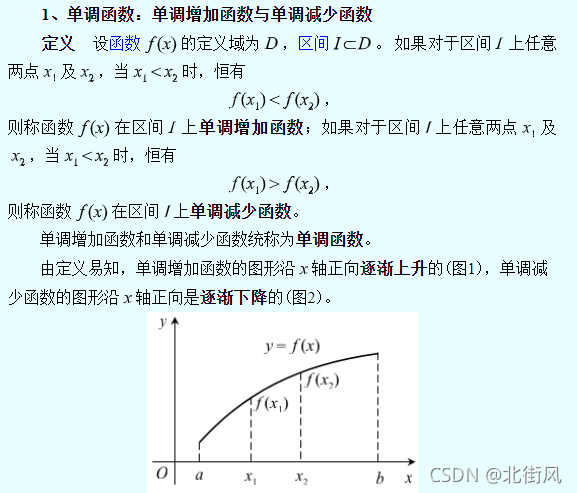
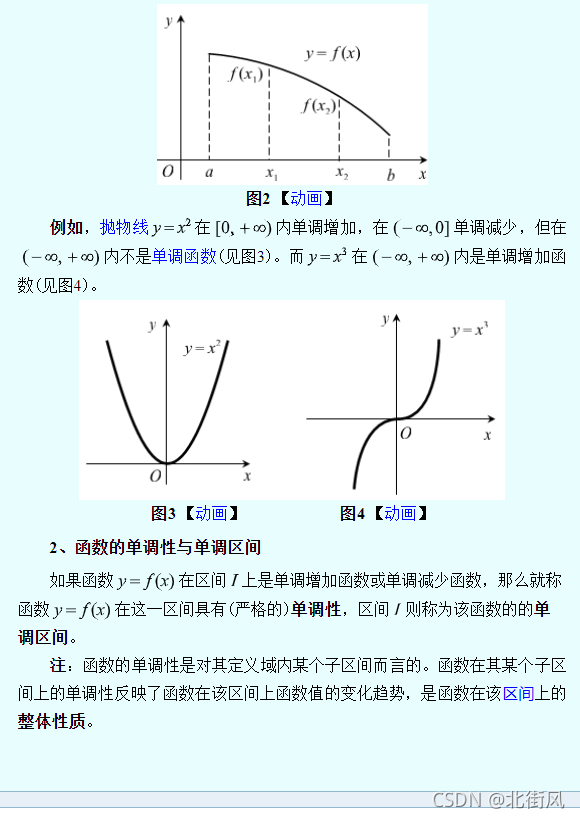

x的负一次方等于x的一次方分之1;即:1/x;
二次根式的分母有理化及其常用方法

对数函数的运算法则
8、函数的周期性
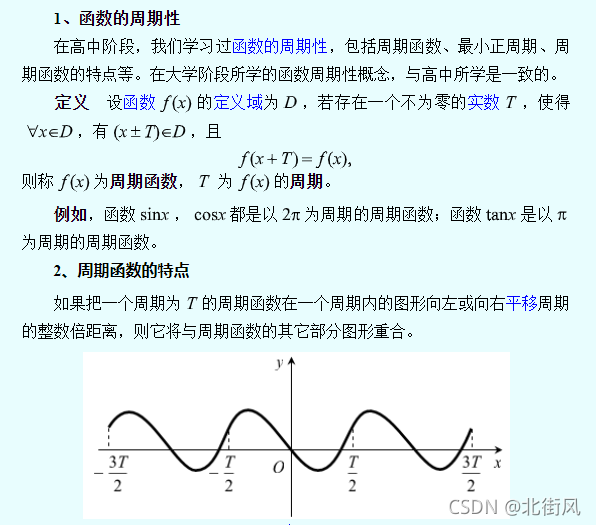

质数与合数,自然数的分类,找质数与合数的方法
两函数奇偶性的运算性质:
(1) 两个奇函数的和仍为奇函数;
(2) 两个偶函数的和仍为偶函数;
(3) 两个奇函数的积是偶函数;
(4) 两个偶函数的积是偶函数;
(5) 一个奇函数与一个偶函数的积是奇函数。
二、映射与集合
在数学里,映射是个术语,指两个元素的集之间元素相互“对应”的关系,为名词。映射,或者射影,在数学及相关的领域经常等同于函数。 基于此,部分映射就相当于部分函数,而完全映射相当于完全函数。

- 单射:指将不同的变量映射到不同的值的函数。
- 满射:指陪域等于值域的函数。即:对陪域中任意元素,都存在至少一个定义域中的元素与之对应。
- 双射(也称一一对应):既是单射又是满射的函数。直观地说,一个双射函数形成一个对应,并且每一个输入值都有正好一个输出值以及每一个输出值都有正好一个输入值。 (在一些参考书中,“一一”用来指双射,但是这里不用这个较老的用法。)