一、提要
对于显函数,其曲线可以通过给出定义域和对应的函数值画出。然而对于一些隐函数,不能显式表达,其曲线如何画出?如果从定义域内,逐点求出函数值,然后画出点序就不是一个很好的主意。用计算方法求出所有点,然后再过滤,反而是一个好的解决方法。本文按照
二、基于隐函数的变换
2.1 法1:平面上等高线模型
给出一个隐函数如下:
对于这样的隐函数方程,很容易写成函数:
z是平面x-0-y上的高度函数,那么,求出平面上任意点(x,y)的高度,将高度为0的点取出,就是原方程轨迹。
import matplotlib.pyplot as plt
import numpy as np# 作点
x = np.linspace(-1, 15, 1000)
y = np.linspace(-1, 15, 1000)# 构造网格
x, y = np.meshgrid(x, y)
z = 0.5 * x - 0.3 * np.log1p(x) + 0.3 * y - 0.1 * np.log1p(y) - 1plt.contour(x, y, z, [0,1,2,3])
plt.show()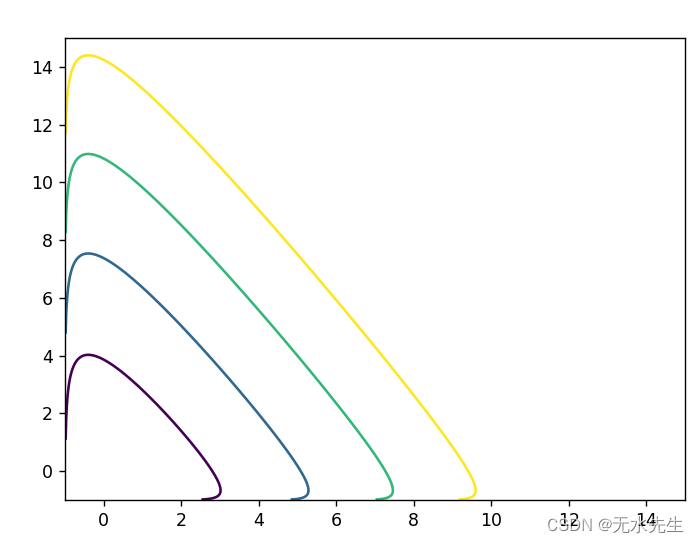
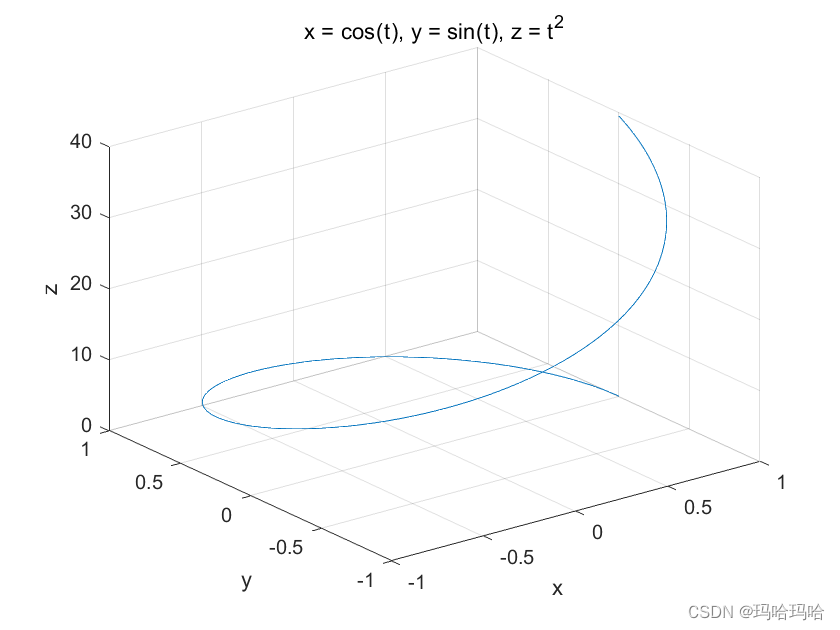
2.2 法2:用三维坐标表现
对于函数,
用图像分割的方法进行,依然转化成:
画出图像的代码:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Ddef getZ( X, Y ):# gray = np.zeros_like(X)gray = X**2+X+1 - Y**3return grayX = np.linspace(0,100,1001)
Y = np.linspace(0,200,2001)
X, Y = np.meshgrid(X,Y)
Z = getZ( X,Y )
S = np.where(np.abs(Z)<0.5,10,0)
figure = plt.figure()
# 画出三维坐标系:
axes = Axes3D(figure)axes.plot_surface(X, Y, S, cmap='rainbow')
# 显示图形:
plt.show()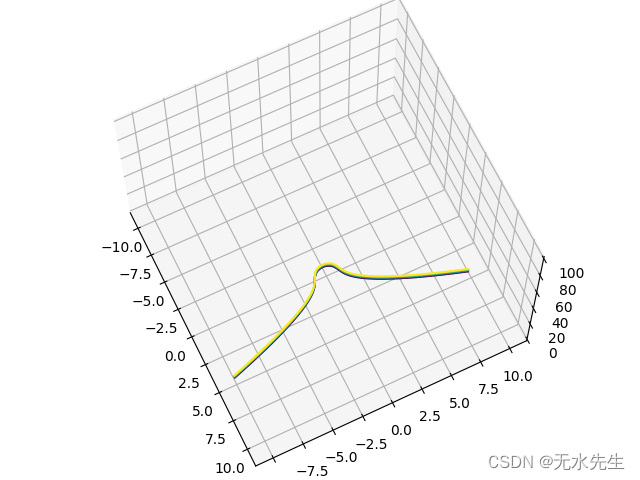
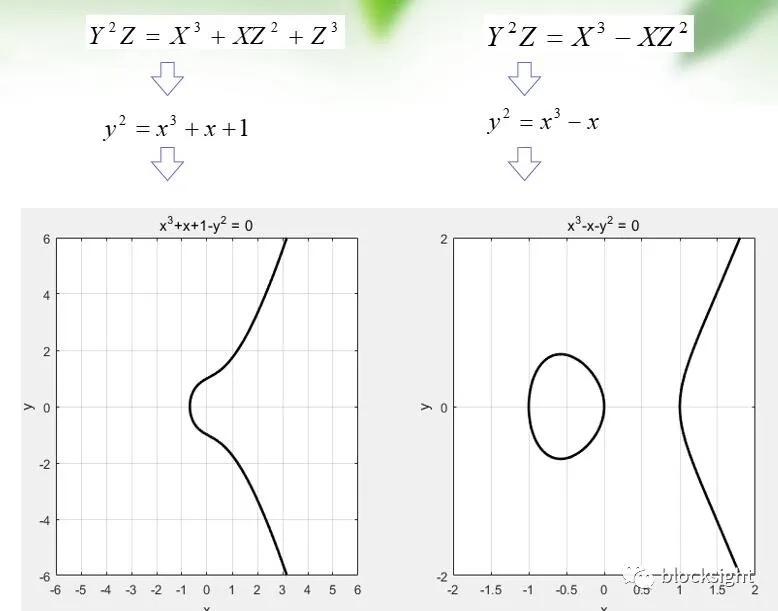
三、椭圆曲线方程
标准的椭圆曲线方程,
![]()
称为威尔斯特拉斯方程(Weierstrass),满足:
1.椭圆曲线方程是一个齐次方程
2.曲线上的每个点都必须是非奇异的(光滑的),偏导数FX(X,Y,Z)、FY(X,Y,Z)、FZ(X,Y,Z)不同为0
3.圆曲线的形状,并不是椭圆的。只是因为椭圆曲线的描述方程,类似于计算一个椭圆周长的方程故得名
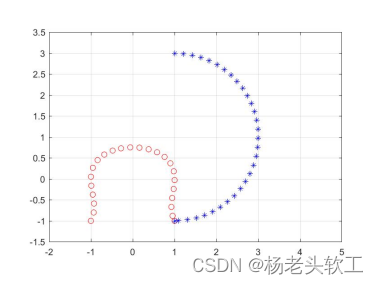
下面两个不是椭圆曲线(在零点不光滑)
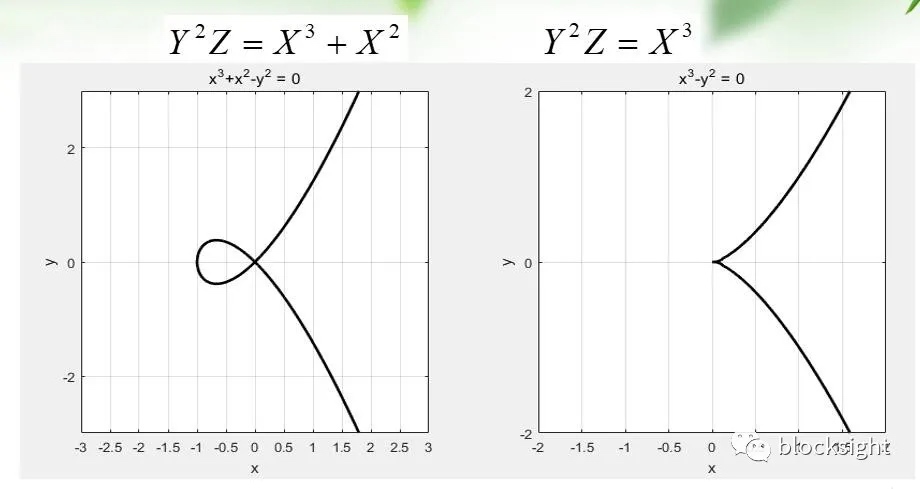
以上椭圆方程也可以用所给出的代码实现绘图。