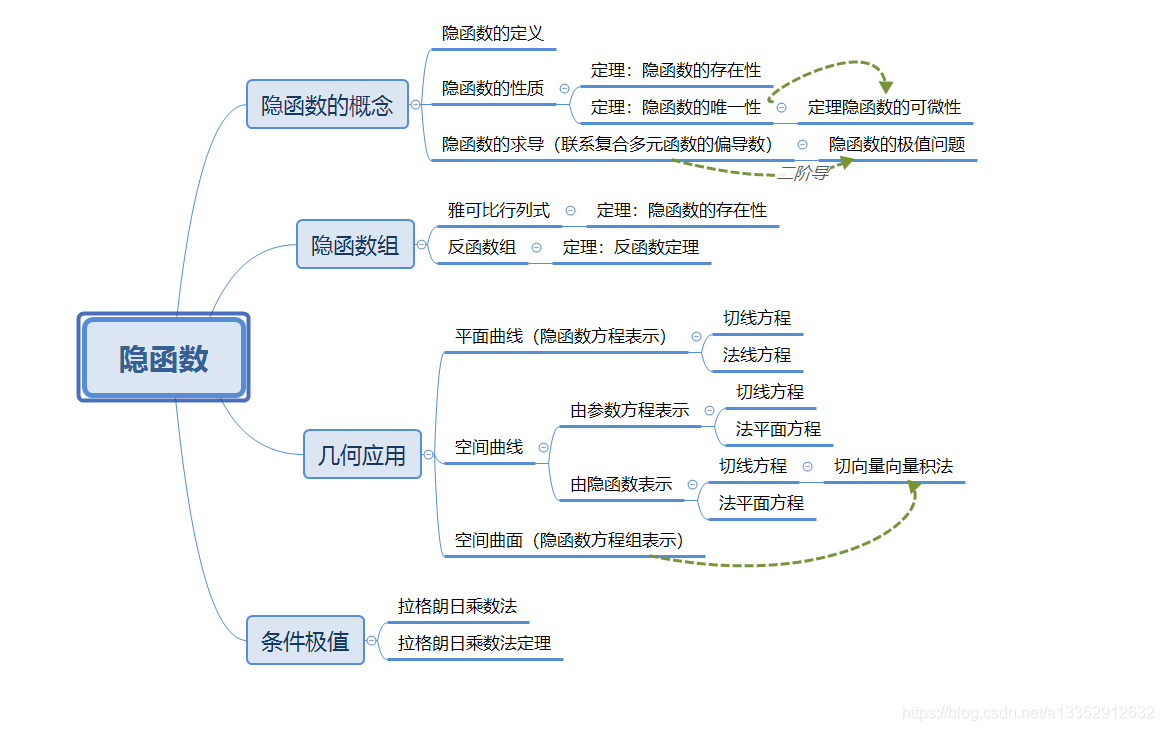
简介:用多元函数(隐函数中自变量和因变量同时存在的表达式的作为多元函数的表达式)的思维来分析隐函数
隐函数的概念
|| 定义:隐函数的定义(一个多元函数F(x, y)构成的方程F(x, y) = 0,隐含了一个隐函数y=f(x))
显函数的表达式是包含自变量的某个算式,而隐函数中自变量与因变量之间的对应法则则是由一个方程式来确定的。
|| 定理1:隐函数的存在性条件(既然隐函数要表现成等于0的方程形式,那么其零点对于隐函数的存在性非常重要)
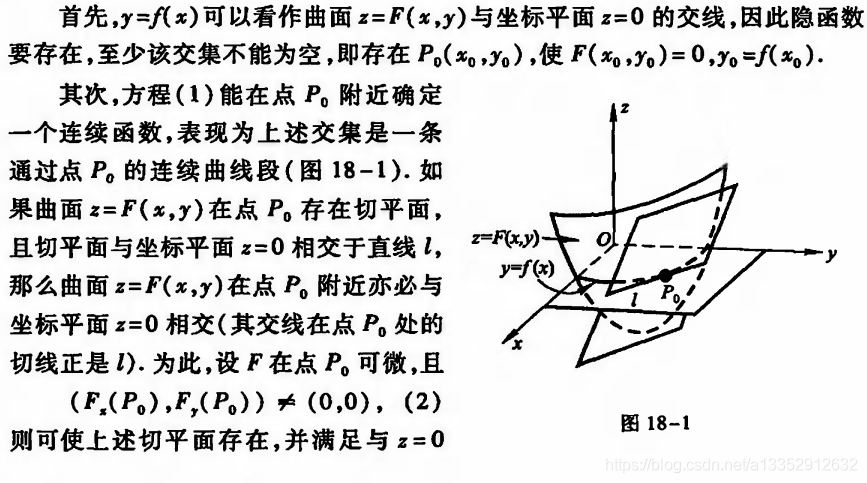
|| 定理2:隐函数存在唯一性定理

(总结:1,存在零点(x0, y0)。2,函数F在某一区域D上有关于y的连续偏导数且该偏导数在零点(x0, y0)不为0)
|| 定理3:隐函数可微性定理(同多元函数的可微性定理)

(总结:唯一性定理,再加上函数F在某一区域D上有关于x的连续偏导数,则得出可微性)
|| 隐函数的求高阶导:(看成复合多元函数的高阶偏微分即可)
一阶导:
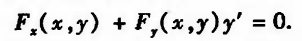
二阶导: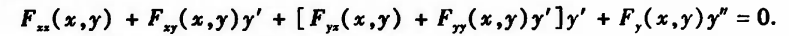
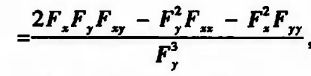
|| 定理4:隐函数的极值问题(即由复合多元函数的偏微分二阶导,与0大小比较)
(注意:复合多元函数中的导数无法求出,故找极值时使用的是黑赛矩阵)

|| 多元隐函数,与其唯一存在性和可微性的定理
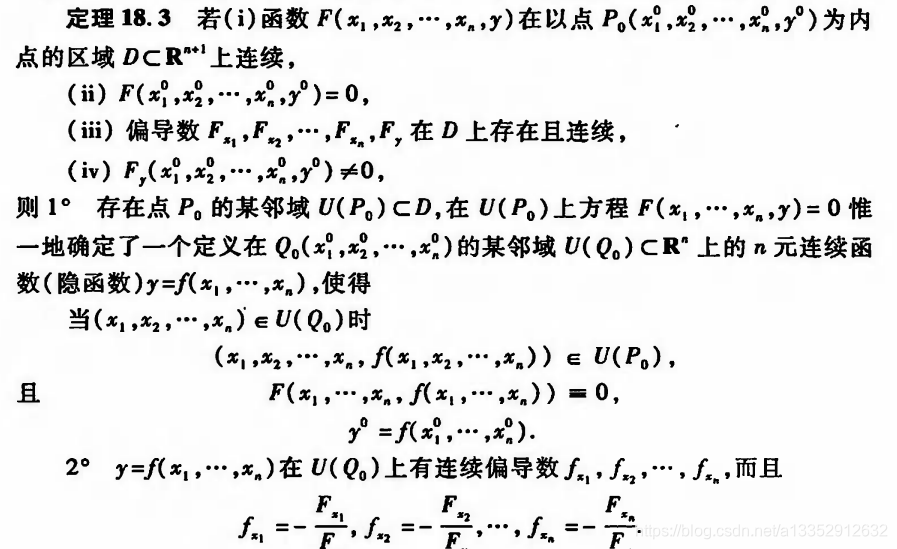
隐函数组
|| 定义:隐函数组的定义

(注意更多变量确定的的隐函数组将在以后用向量讨论)
|| 函数行列式(雅可比行列式)
隐函数组偏导数系数组成的行列式

|| 定理5:隐函数组定理


|| 反函数组

|| 定理6:反函数组定理


(注意:由上式可以看出,互为反函数的函数,他们的雅可比行列式互为倒数:)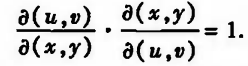
几何应用
由隐函数(组)确定的曲线和曲面,在且他们的切线或切平面式都要使用隐函数(组)的微分法
方程某些时候与函数表示了相同的几何意义,由此推出了公式
|| 平面曲线的切线与法线方程:(隐函数 F(x,y)= 0确定的平面曲线)
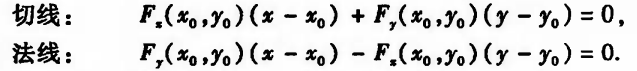
|| 空间曲线的切线:(参数方程 L:x=x(t), y=y(t), z=z(t), a ≤ t ≤ b 确定的空间曲线)
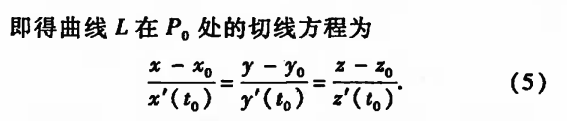
|| 空间曲线的法平面:(参数方程 L:x=x(t), y=y(t), z=z(t), a ≤ t ≤ b 确定的空间曲线)
(过点p0的法平面即所有与p0的切线相垂直的直线所构成的平面)
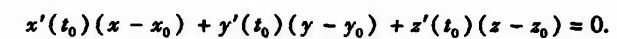
|| 空间曲线的切线和法平面( 隐函数方程组确定的空间曲线)

切线方程与法平面方程:

|| 隐函数确定的曲面的切平面和法线
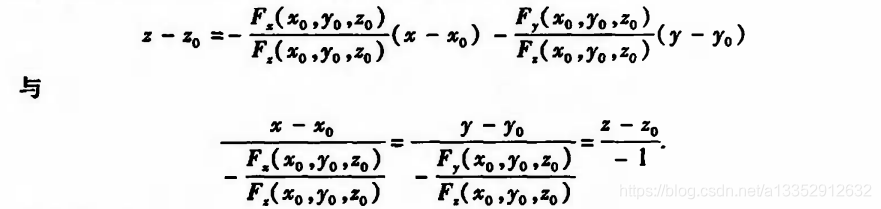
另一种形式:
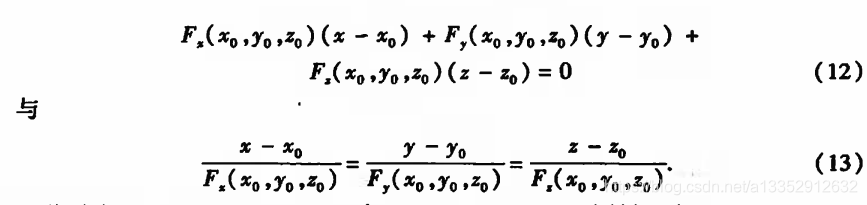
|| 再谈隐函数方程组确定的空间曲线的切线和法平面
因为隐函数方程组确定的空间曲线L 可以 看作是两个隐函数确定的两个曲面的交线L,易知曲线L在P0的切线与两个曲面在p0的法线都垂直。两个法线的法向量为n1 = (Fx, Fy, Fz) | p0 与 n2 = (Gx,Gy,Gz), 故L在p0的切向量等于n1与n2的向量积

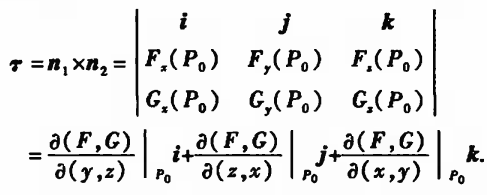
条件极值
极值限定的搜索条件不再只是目标函数的定义域,还有许多其他条件
附有约束条件的极值问题就叫做条件极值问题
|| 条件极值问题的一般形式:(以前一般使用的是消元法)

|| 拉格朗日乘数法(不依赖消元法求解条件极值问题)
辅助函数 L 称为拉格朗日函数,辅助变量 λ 称为拉格朗日乘数
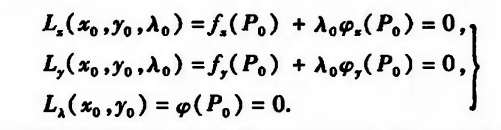

(公式的推导过程为:使用辅助函数 L 联系隐函数, 其中用到等高线的几何关系)
|| 定理7:拉格朗日乘数法的定理