一、引言

fimplicit3功能是绘制二元隐函数的曲面图形。
类似于一元函数分为显函数和隐函数，二元函数也有显函数和隐函数之分。形如z=f(x,y)的二元函数称为显函数，而由三元方程f(x,y，z)=0确定的二元函数称为隐函数。
二元函数对应的几何图形是空间曲面，也称为三维曲面。
对于二元显函数绘图，可以使用matlab命令mesh、fmesh、surf和fsurf以及相应的扩展函数来实现。
对于隐函数，有些可以显化，此时可以使用上述matlab绘图命令来绘图，但是仍旧有很多二元函数不易显化，这就需要使用fimplicit3实现曲面的绘制。

二、implicit3基本语法

fimplicit3基本语法主要包括以下几种：
1）fimplicit3(@(varibles)function)
其中varibles是方程f( ·, ·, · ) = 0中全部的变量，function是确定隐函数的三元方程f( ·, ·, · ) = 0中左端项，也就是三元函数f( ·, ·, · )。
此语法没有给出自变量的取值范围，如果因变量|z|的最大值可以达到5，则以此来限制自变量的取值范围，否则限制自变量的取值范围为[-5,5]。
2）fimplicit3(@(varibles)function, interval, linespec)
其中：
varibles是方程f( ·, ·, · ) = 0中全部的变量，function是确定隐函数的三元方程f( ·, ·, · ) = 0中左端项，也就是三元函数f( ·, ·, · )；
interval表示方程中三个变量的区间；
linespec表示图元的属性。
补充：当f( ·, ·, · )中只给出一组取值范围时，是表示三个变量的取值范围相同，以竖坐标z优先。
3）fimplicit3(@(varibles)function, name,value)
其中
varibles是方程f( ·, ·, · ) = 0中全部的变量，function是确定隐函数的三元方程f( ·, ·, · ) = 0中左端项，也就是三元函数f( ·, ·, · )；
name表示曲面属性的名称；
value是name的取值。
★★★ 参数name的常见取值有：
‘EdgeColor’ 表示曲面上网格线的颜色
‘FaceAlpha’ 表示透明度
‘FaceColor’ 表示曲面的颜色
‘MeshDensity’ 表示每个方向上的计算点数
‘LineStyle’ 表示网格线的线型
‘LineWidth’ 表示网格线的线条宽度
补充：
fimplicit3参数function的定义形式即可以是使用@法定义的，也可以是通过syms定义符号变量而得到的符号函数，
例如：
fun = @(x,y,z)x.^2 + y.^2 - z.^2
或者：
syms x y z;
fun = x^2 + y^2 - z^2;
注意：使用@法生成的符号函数，必须在变量的后面加. ，表示数组元素的运算，否则会提示告警信息。

三、implicit3绘图示例

Demo1：绘制如下方程表示的曲面图形。

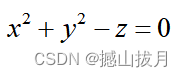
%示例代码
fimplicit3( @(x,y,z)x.^2 + y.^2 - z ); 
axis equal
title( 'x^2 + y^2 - z = 0：旋转抛物面' );
%运行结果

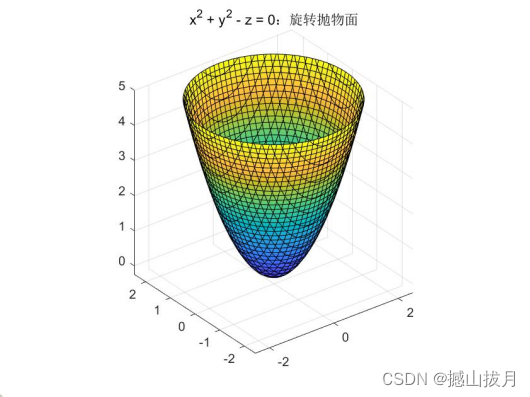
Demo2:绘制如下方程表示的曲面图形。

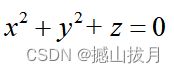
%示例代码
fun = @(x,y,z)x.^2 + y.^2 + z
fimplicit3( fun ); 
axis equal
title( 'x^2 + y^2 + z = 0：旋转抛物面' );
%运行结果

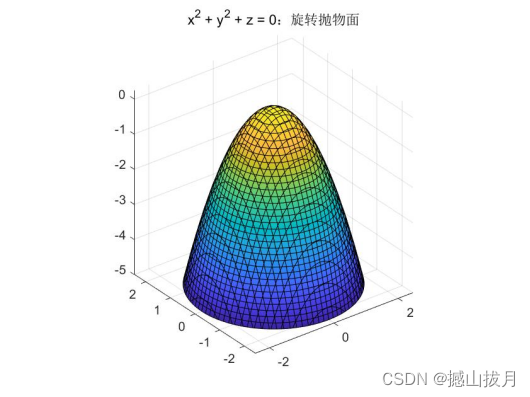
从以上两个demo可以发现，|z|的最大值达到了5，此时由z限制了x和y的取值范围。

Demo3:绘制如下方程表示的椭球面曲面图形。

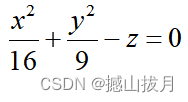
%示例代码
syms x y z;
fun = x^2/16 + y^2/9 - z
fimplicit3( fun ); 
axis equal
title( 'x^2/16 + y^2/9 - z = 0：椭圆抛物面' );
%运行结果

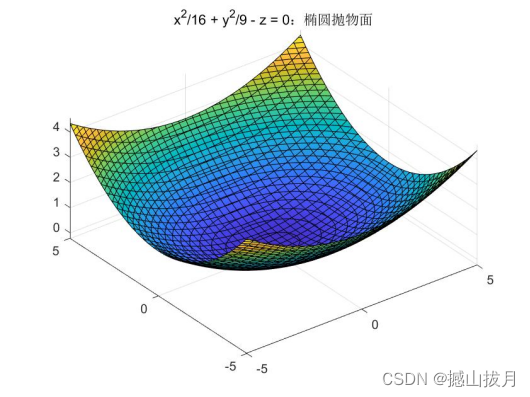
由此图可以看出，x和y的取值范围是[-5,5]，而z的取值最大值小于5，曲面图形看起来也不够美观，为了改善这个问题，可以使用下面的语法来实现。

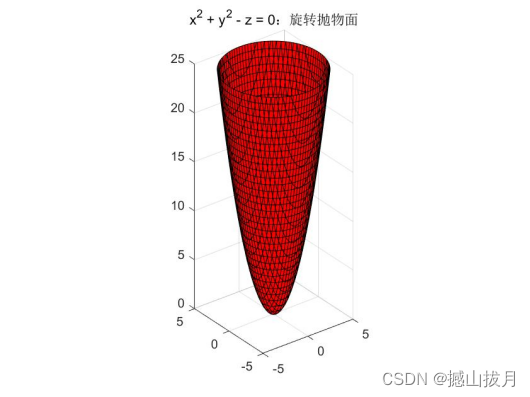
Demo4:绘制如下方程表示的旋转抛物面图形，给定变量的取值范围，并指定绘图的颜色。

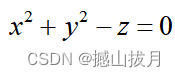
%示例代码
fimplicit3( @(x,y,z)x.^2 + y.^2 - z, [-5, 5, -5, 5, 0, 25], 'r' ); 
axis equal
title( 'x^2 + y^2 - z = 0：旋转抛物面' );
%运行结果

Demo5：绘制如下方程表示的曲面图形，给定一组变量取值范围，并指定绘图的线元。

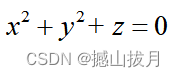
%示例代码
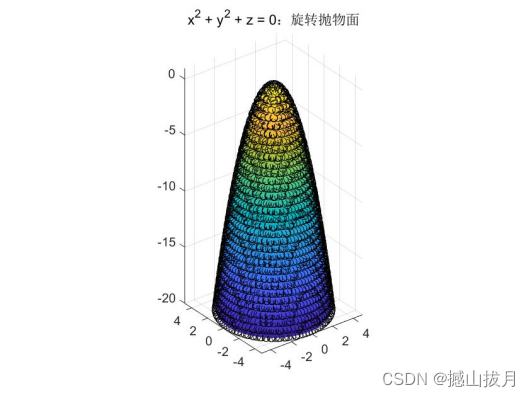
fimplicit3( @(x,y,z)x.^2 + y.^2 + z, [-20, 5], 'o' ); 
axis equal
title( 'x^2 + y^2 + z = 0：旋转抛物面' );
%运行结果

Demo6：绘制如下方程表示的曲面图形，指定绘图的线元颜色。

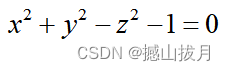
%示例代码
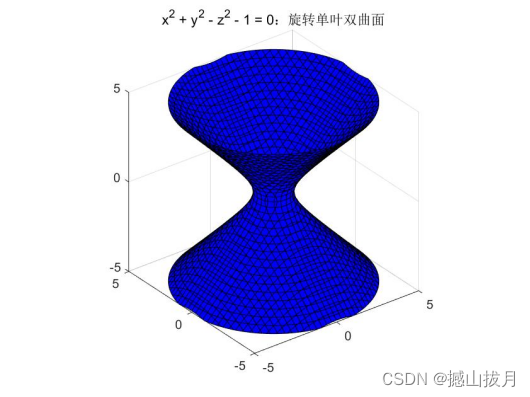
fimplicit3( @(x,y,z)x.^2 + y.^2 - z.^2 - 1, 'b' ); 
axis equal
title( 'x^2 + y^2 - z^2 - 1 = 0：旋转单叶双曲面' );
%运行结果

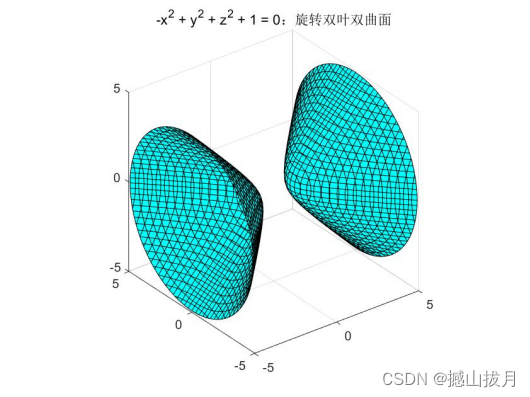
Demo7：绘制如下方程表示的曲面图形，指定绘图的线元颜色。

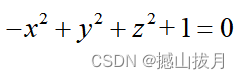
%示例代码
fimplicit3( @(x,y,z)-x.^2 + y.^2 + z.^2 + 1, 'c' ); 
axis equal
title( '-x^2 + y^2 + z^2 + 1 = 0：旋转双叶双曲面' );
%运行结果

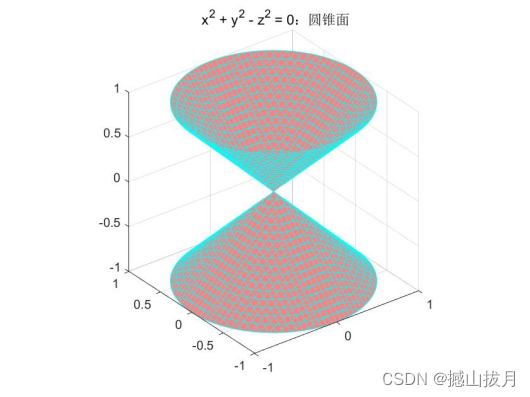
Demo8：绘制如圆锥面的曲面图形，指定绘图的线元颜色、曲面颜色和变量取值范围。

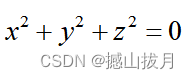
%示例代码
syms x y z
fun = x^2 + y^2 - z^2;
fimplicit3( fun,[ -1, 1 ], 'EdgeColor', 'c', 'Facecolor', [ 1, 0.5, 0.5 ] );
axis equal
title( ' x^2 + y^2 - z^2 = 0：圆锥面' )
%运行结果

Demo9：绘制如下方程对应的马鞍面图形。

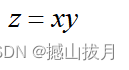
%示例代码
fun = @(x,y,z)x.*y - z;
fimplicit3( fun, 'FaceColor', 'b', 'FaceAlpha', 0.5 ); 
axis equal
title( 'z = x * y：马鞍面' );
xlabel( 'x' )
ylabel( 'y' )
zlabel( 'z' )
view( [-0.2, 0.8, 0.5] );%调整视角
%运行结果

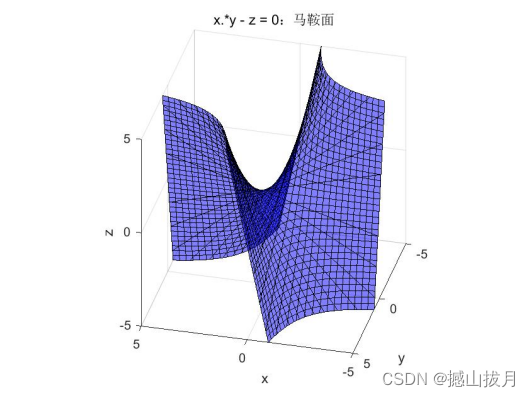
Demo10：绘制马鞍面图形。

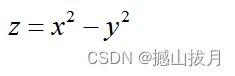
%示例代码
fun = @(x,y,z)x.^2 - y.^2 - z;
fimplicit3( fun, [ -10, 10 ], 'EdgeColor', 'None', 'FaceAlpha', 0.8 ); 
axis equal
title( 'z = x^2 - y^2：马鞍面' );
xlabel( 'x' )
ylabel( 'y' )
zlabel( 'z' )
view( [-0.2, 0.8, 0.5] );%调整视角
cmap = colorbar
%运行结果

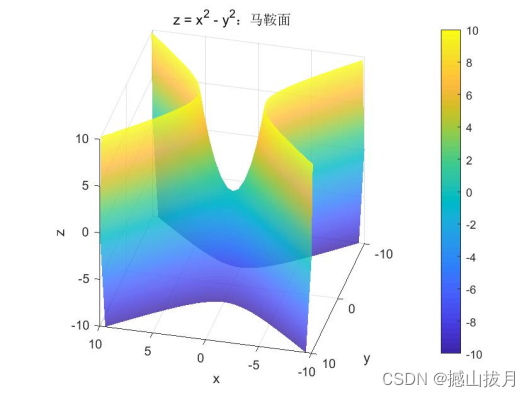
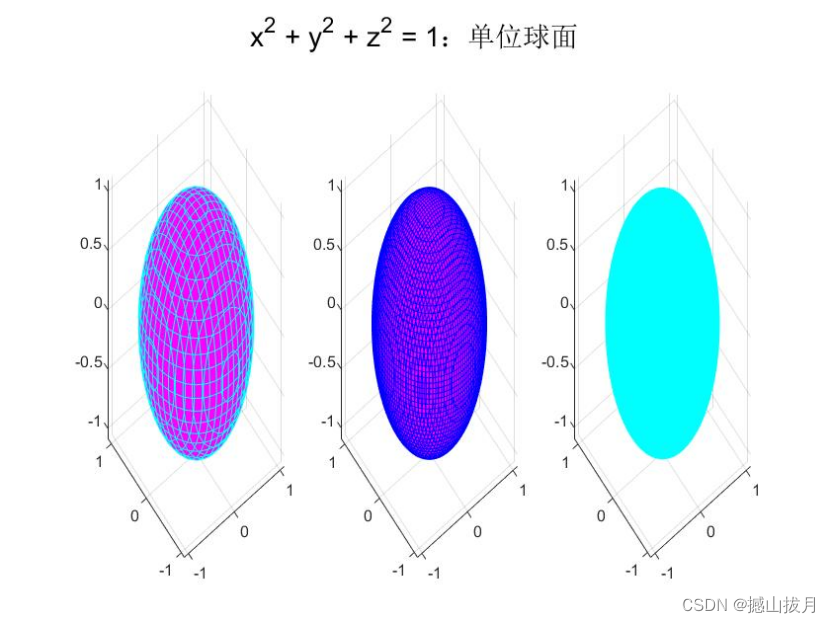
Demo11：采用不同的颜色和网格数绘制单位球面。

%示例代码
subplot( 1, 3, 1 )
syms x y z
fun = x^2 + y^2 + z^2 - 1;
fimplicit3( fun, 'EdgeColor', 'c', 'Facecolor', 'm', 'MeshDensity', 20 );
subplot( 1, 3, 2 )
fimplicit3( fun, 'EdgeColor', 'b', 'Facecolor', 'm', 'MeshDensity', 50 );
subplot( 1, 3, 3 )
fun = @(x,y,z)x.^2 + y.^2 + z.^2 - 1;
fimplicit3( fun, 'EdgeColor', 'None', 'Facecolor', 'c' );
suptitle( 'x^2 + y^2 + z^2 = 1：单位球面' )
%运行结果