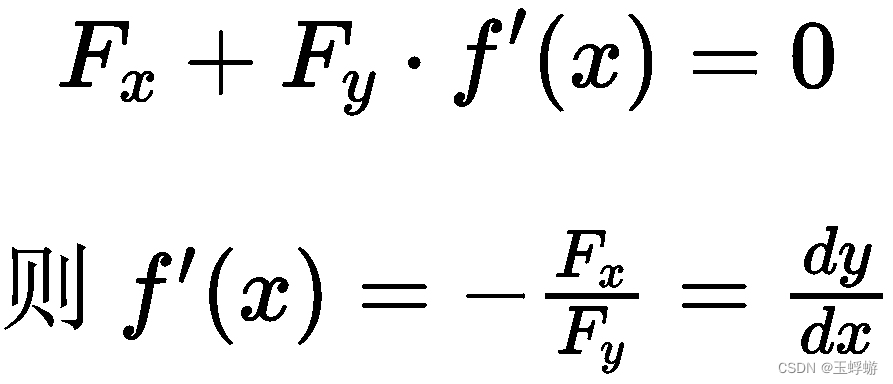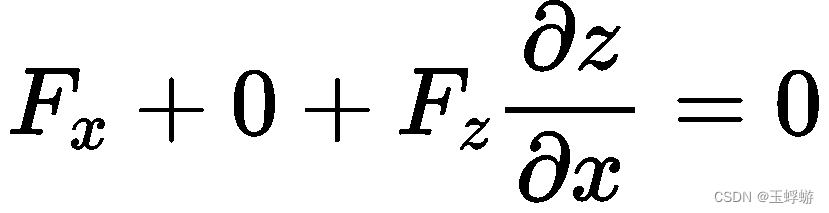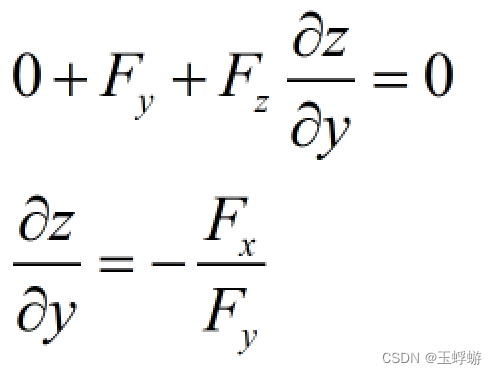目录
什么是隐函数
一个方程,两个未知数
一个方程,三个未知数
方程组求偏导
隐函数求导一般有两种情形,一种是单个方程,另一种是方程组。下面来介绍这两种情形的求导方法。
什么是隐函数
首先我们要明确:什么是隐函数?什么是显函数?
容易看出,式子 F(x,y) = 0 与 y = f(x) ,在本质上是一样的,都确定了x与y的关系。只不过两个式子的表现形式不同,y = f(x) 这个式子很明显y是因变量,x是自变量,是显式的;而将其移项,y - f(x) = 0,也即F(x,y) = 0,这种式子谁是谁的函数关系并不清楚,所以是隐式的。
所以F(x,y) = 0这种形式的当然是隐函数喽。然而,大多数方程不能表现为显式的,甚至也不能确定y与x的一一对应关系,所以我们不仅要掌握显式函数求导的链式法则,也要知道隐函数该如何下手求导。
一个方程,两个未知数
隐函数存在定理1给出了公式:
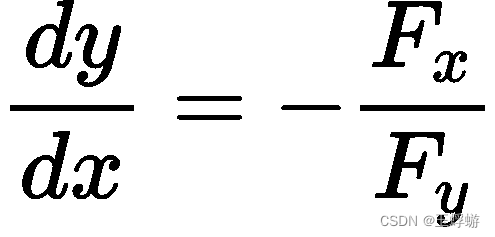
这个公式如何证明已经超出了我的能力范围,暂且仅给出该公式的推导吧。
由于y是x的函数,则 F(x,y) = 0 可以写成 F(x,f(x)) = 0,则式子两边同时对x求导得:
求二导的时候也是如此,直接对一阶导求二导,同样把y看成x的复合函数,即

一个方程,三个未知数
我们来将二元的隐函数推广到三元,由隐函数存在定理2给出公式:
对于方程 F(x, y, z) = 0 ,
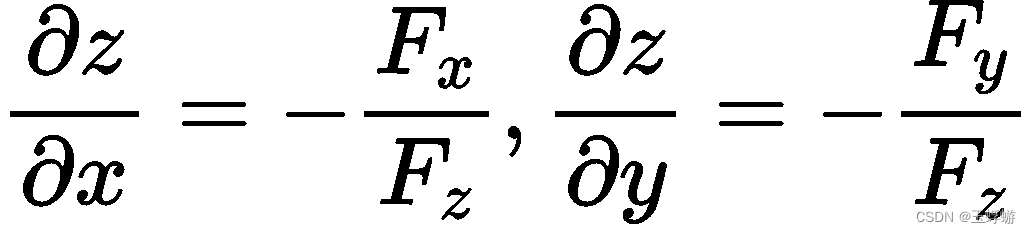
在这里我也只能仅仅给出推导。在这个方程 F(x ,y, z) = 0 中,总共有三个未知数,有一个方程,则有一个因变量,那么就有3-1=2个自变量,如果将z看成因变量,将x和y看成自变量的话,即z = f(x, y) ,式子可以写成 F(x, y, f(x, y)) = 0 ,接着,等式两边同时对x求导:
,
同理,等式两边同时对y求导:
求二导和二元隐函数方法是一样的,这里就不作赘述了。
方程组求偏导
F(x, y, u, v) = 0
G(x, y, u, v) = 0
在这个方程组中,总共有4个未知数,有两个方程,则有两个因变量,那么还有两个自变量,所以该方程组确定了两个二元隐函数。那么我们不妨假设u,v是因变量,x,y是自变量,那么由该方程组确定的两个隐函数为u = f(x, y), v = f(x, y), 因此,方程组可写为:
F(x, y, f(x,y), g(x,y)) = 0
G(x, y, f(x,y), g(x,y)) = 0
然后方程组的等式两边同时对x求导,可以利用复合函数的求导法则链式法则:
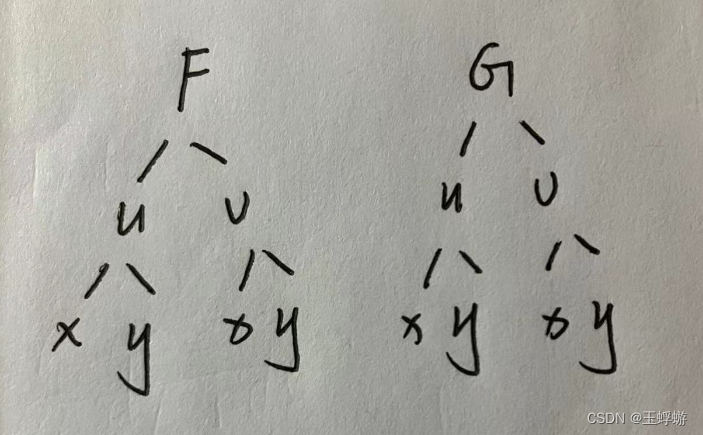
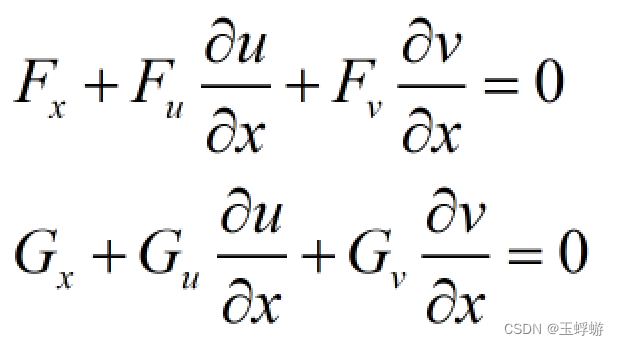
接下来,就是分别计算u,v对x的偏导了。这里提供两种方法,一种是高中学习的消元法,另一种是运用克拉默法则。消元法比较简单,但是计算起来比较复杂,不太推荐,下面重点介绍第二种方法。
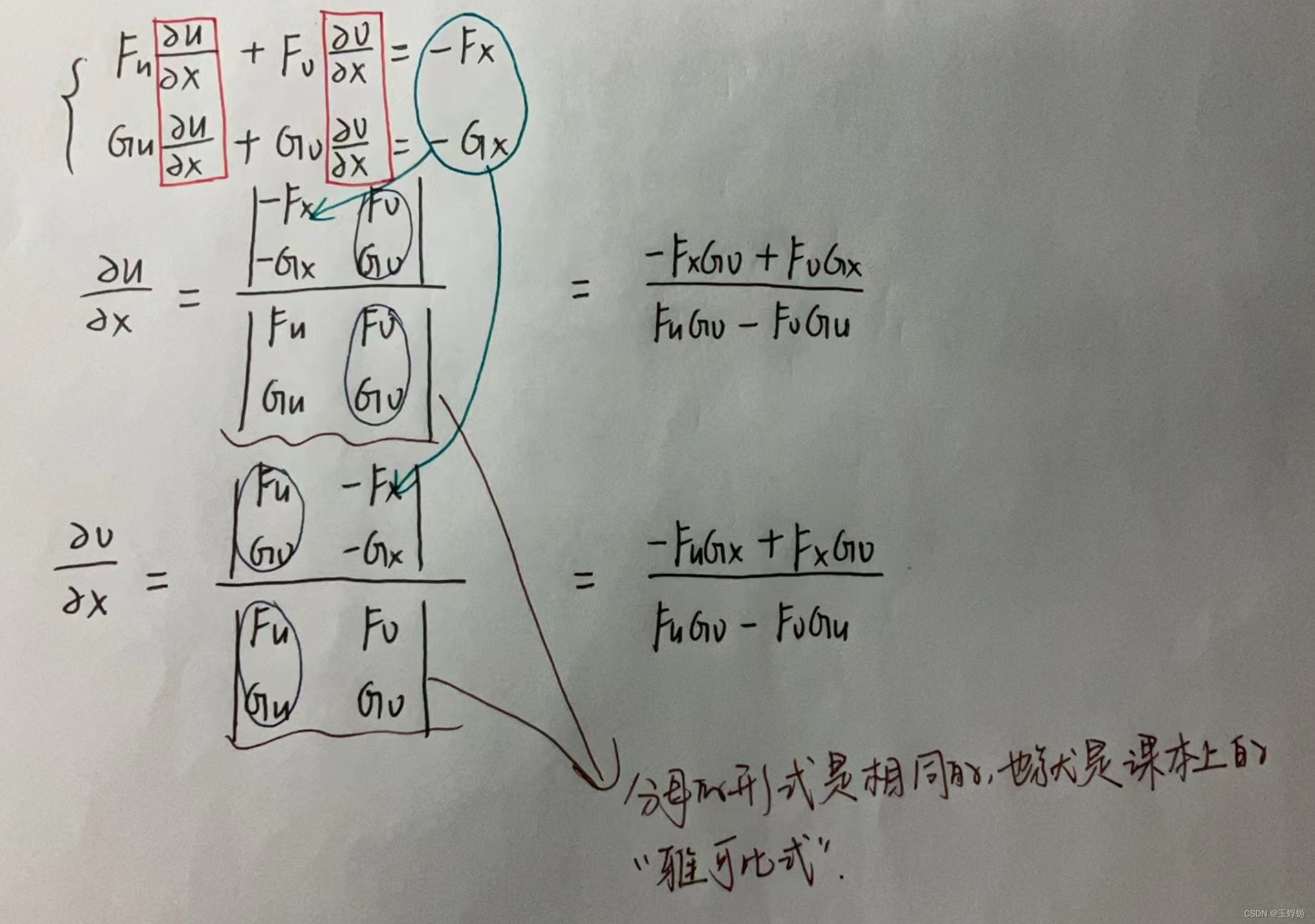
对式子进行移项处理后就可以使用克拉默法则来算了。
PS:我之前一直不理解为什么方程组中的求导是复合函数求导,而将方程组中的式子拿出来求偏导就只能用公式法了,不能使用复合函数求导。今天问了高数老师,老师告诉我:“那是数学家整出来的,给你解释了也没啥意思,会做题就行了。”所以目前我还是不理解,但是确实不影响做题,老师既然实力劝退,那我还是不管它了吧,它目前超出了我的能力范围。