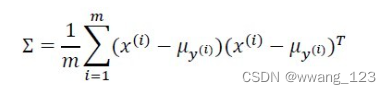本文诞生的缘由

由于布谷鸟算法比较新，所以国内外的网上对于该算法的介绍都比较少，虽然算法整体的思想看起来简单，但真正落实到实践时往往发现有些细节还是不甚清楚。令人尴尬的是，我搜索了国内外对于布谷鸟算法的教程，这些教程恰恰点到算法思想上就止住了，并且给出的代码千篇一律地还是Xin-She Yang（布谷鸟算法提出者之一）给出的matlab代码¹，对初学者很不友好，于是我就打算写一篇教程，通过详细地举一个例子来带大家入门布谷鸟算法，并且我写了份python代码（可直接运行），需要者可在下面的github链接中自取。

布谷鸟算法思想简介

布谷鸟算法的启发当然来自于布谷鸟，因为布谷鸟这种鸟很有意思，生出来的孩子自己不养，直接被扔到其他鸟的鸟巢中去了，但有时候，这些布谷鸟蛋会被被寄宿的那些鸟妈妈发现，然后就被抛弃，有时候，这些宿主会直接放弃整个鸟巢寻找新住处。然而道高一尺魔高一丈，有些品种的布谷鸟生下来的布谷鸟蛋的颜色能和去寄宿的鸟的鸟蛋颜色很相似，并且布谷鸟的破壳时间往往比那些宿主的鸟蛋早，这样，一旦小布谷鸟破壳，它就会将一些鸟蛋扔出鸟巢去以求获得更多的食物，并且，小布谷鸟能模拟宿主鸟孩子的叫声来骗取更多的食物！简单来说，就是如何更高效地去骗吃骗喝。

图1 寄宿到其他鸟的布谷鸟蛋

这时，心急的朋友可能会问，这和最优化有啥蛋关系呢？如果光让我看到这种自然现象我也很难和最优化联系起来，但有些细心的人做到了。我们现在来简单概括一下他们是咋联系起来的。

他们假设最初在可行域内随机生成一组点（布谷鸟）
计算这些点的适应值（鸟的健康程度），并记录下最健康鸟的位置及其适应值
然后通过某种方式更新这些点的位置（布谷鸟找其他鸟的鸟巢下蛋）
这些寄宿到其他鸟的布谷鸟蛋有一定几率被抛弃，这时布谷鸟需要找新的位置来下新的布谷鸟蛋，没被发现的布谷鸟蛋就保持原样（也就是保持每次迭代的点的总数不变）
这些布谷鸟蛋成功被孵化然后长大，原有的布谷鸟则会死去，现在评估新的这些点的适应值（新长大的布谷鸟的健康程度），若比原有记录下最好适应值要好则更新最好适应值
新的这批布谷鸟从第3步继续迭代，直至满足迭代次数或精度要求

一头雾水？别怕，后面一个例子就懂了！

更新位置的方式

细心的朋友在看上面算法步骤时可能会问，以某种方式更新位置，是啥子方式呢？更新位置的算法同样很重要，它也会关系到最后算法的收敛速度，在上述的算法步骤中，我们在第3步和第4步都需要更新点的位置，现在就来解答这个问题。其实这些更新点的方式说的直白些其实很简单，就是让这些点乱走，当然它有个洋气的名字（random walk），乱走的方式也很简单粗暴，随机生成一个方向和长度，叠加到原有点上就成了新的点，但是需要指出的是，这个随机生成的方向和长度都是有讲究的，有研究发现通过莱维飞行（Levy Flight）的方式能比较有效地去寻找全局最优解而不至于陷入局部最优解中，并且它和布谷鸟算法配合达到了相当不错的效果，接下来就是解答什么是莱维飞行了。

莱维飞行

在介绍莱维飞行相关公式之前，我们先来简单说一下它背后的思想，莱维飞行是由较长时间的短步长和较短时间的长步长组成，说起来很拗口，我们先来看一下它的演示图吧：

图2 莱维飞行动画

从上面的动画中我们可以看到，点大多数时间都只有小距离移动，偶尔会有大距离移动的情况。这和自然界中大多数动物觅食方式方式类似，也就是找到一块区域后细致的查找猎物，如果没找到，就换一片区域找。
那么，该如何实现这种移动方式呢？我们现在假设我们就是捕食者，需要捕猎去了，但尚不清楚猎物在哪，那好，我们先随机选个方向（服从均匀分布，因为在不知道任何信息前提下，对于我们来说各个方向存在猎物的可能性相等），接下来就得确定要走多远了，根据上面的思想，Levy分布要求大概率落在值比较小的地方，而小概率落在值比较大的地方，Mantegna就提出了近似满足这种分布的计算公式（levy分布很难满足，有兴趣的小伙伴可以查阅相关资料）：
$s=\frac{u}{\left | v \right |^{\frac{1}{\beta }}}$
(说明：u服从 $N(0,\sigma _{u})$ 正态分布，v服从 $N(0,\sigma _{v})$ 正态分布，而 $\sigma _{u} = \left \{ \frac{\Gamma (1+\beta )\sin (\frac{\pi\beta }{2})}{\Gamma \left [ \frac{(1+\beta )}{2}\beta \cdot2^{\frac{(\beta -1)}{2}} \right ]}\right \}^{\frac{1}{\beta }}$ ， $\sigma _{v}=1$ ，其中 $\Gamma (z)=\int_{0}^{\infty }\frac{t^{z-1}}{e^{t}}dt$ ， $\beta$ 取值最好落在(1,2)上)。上面的公式乍一看十分复杂，但幸运的是，无论是matlab还是python，关于正态分布和 $\Gamma$ 函数都有现成的函数，我们做伸手党即可。而这个公式咋来的便是数学家的事情了，我也不懂啊(ಥ_ಥ)，但我们可以编个小程序直观地感受到其生成的步长确实短步长多，长步长少（可见上面的动画）。概括地来讲，实现莱维飞行，一要通过均匀概率分布生成一个方向，二要确认步长！

局部随机行走

我们再来介绍一种随机行走的方法（random walk），但这种方法只适用于局部，很容易陷入局部最优解，优点是比较稳定，因为是局部走嘛。它的计算公式如下：
$x_{i}^{t+1}=x_{i}^{t}+\alpha s\bigotimes H(p_{a}-\epsilon )\bigotimes (x_{j}^{t}-x_{k}^{t})$
(说明： $x_{i}^{t}$ 是第i个点t时刻的位置， $\alpha$ 是步长系数，也就是让步长增量和你问题的规模相匹配，举个例子，你的问题的规模是个位数级别的，你肯定不希望步长增量是十位数级别或者毫米数级别的，这就需要你适当缩小或扩大步长了，H是跃迁函数，也就是x大于等于1时数值为1，否则为0， $\bigotimes$ 代表点乘， $x_{j}^{t}$ 和 $x_{k}^{t}$ 是t时刻任意选取的两个点)。
相对于莱维飞行的随机性，局部随机行走时已有一定的方向性了，其最大程度地利用已有点的位置信息，新产生的点便是这些已有点的“折中”。

抛出个栗子

看完上面一些理论知识，你可能更晕了，那么，接下来吃下这颗栗子，你可能便会豁然开朗了。

我们要优化的问题是这样的：
$3(1-x)^{2}\cdot e^{-x^{2}-(y+1)^{2}}-10(\frac{x}{5}-x^{3}-y^{5})\cdot e^{-x^{2}-y^{2}}-\frac{e^{-(x+1)^{2}-y^2}}{3}$ 其中x和y都落在(-3,3)上，求其最大值。
为了简化起见，我们这里只取5个点。

第一步、我们现在先在可行域内随机生成5个点：

第二步、计算它们的适应度（适应值函数我们就取为上面那个要优化的函数）：

我们从中挑出最好的并记录下来，我们可以看到，最好的适应值为下标4对应的点，为7.648。

第三步、利用莱维飞行更新点，莱维飞行公式中的 $\beta$ 我们取为1.5，剩下的把公式敲上去获得步长，但是，这样生成的步长的规格是大于问题的规模的，后面我们需要调参，但这里为了简便我就把我后来调出来的结果摆出来，莱维飞行的步长需要乘以系数0.4才能让莱维飞行不至于走的太放飞自我，也不至于走的太畏畏缩缩（多数情况下，系数取为0.1和0.01）。这里我们还用到了一个小技巧，我们当然是希望上一轮产生的最好点能在下一轮保留下来，所以我们可以在步长前乘以个系数 $x_{i}^{上一轮}-x_{best}^{上一轮})$ ，这里的 $i$ 就是步长对应的点下标。当然，有了步长还不够，还得有个步长方向，这个方向我们就用0-1均匀概率分布产生，步长方向（矢量）点乘步长（矢量）就是步长增量。这是莱特飞行更新后的结果：

第四步、接下来，一些布谷鸟蛋可能会被宿主发现并被抛弃，这个抛弃的概率 $P_{a}$ 我们设置为0.25，当有布谷鸟蛋被抛弃时，我们需要寻找新的寄宿地点，而寻找新的寄宿地点的算法就是上面提到的局部随机行走算法，我们可以把 $\alpha$ 这个系数定为1，步长s我们也取为1，后面两个随机选取的点 $x_{j}^{t},x_{k}^{t}$ ，我们通过均匀概率分布选出，这里我们不使用跃迁函数H。更新后的结果如下：

第五步、计算这些新点的适应值，并挑出最大值和记录的最好点的适应值比较，若该轮更新得到的最大值更好，则将该轮得到的最大点设为最好点并记录下来。遗憾的是，这里，该轮点的最大值没有比记录的最好点好，所以我们不用更新最好点的值。

第六步、回到上面的第三步，继续循环直至满足迭代次数要求或精度要求。
补充：由于随机行走（莱维飞行是随机行走的一种特殊形式）可能会超出我们的可行域范围，我们可以利用简单的边界条件，即当点超过下边界时，则用下边界的值代替，同理，当点超过上边界时，则用上边界的值代替。

一些参数的建议

布谷鸟算法提出者之一的Xin-She Yang教授试了多组参数，发现种群规模在15到40，布谷鸟蛋被发现的概率 $p_{a}$ 取0.25时¹ ²，对于大多数优化问题已足够，并且结果和分析也表明收敛速度在一定程度上对所使用的参数不敏感。这意味着对于任何问题都不需要进行仔细地调整。至于迭代次数，我在实验中发现100次的迭代次数已能很好地找到最优解，但迭代次数往往取决你问题的规模，并没有一组所谓的万能参数。

完整的python实现

在这份代码中，我写了详细的注释，每个函数的功能和输入输出参数都有详细的说明，如果对上面的一些讲解还有些疑惑，可以直接查看代码的相关部分，我想应该很快就能茅塞顿开了。下载地址如下：https://github.com/SJ2050SJ/Optimization_Algorithms（如果对你有帮助的话不要忘点个star哦 ! (^_ ^)

运行结果

上面那个优化函数的图像在这篇文章中可以看到遗传算法（白话文版）。在这次测试中，我们选择种群规模为25，迭代次数为100。由精确分析可知，上述优化问题在可行域内的最大值为8.1062，在 $0.0093,1.5814]^{T}$ 上取到，可以看到，我们优化的结果已经很接近精确答案了，并并且每次优化出来的结果很稳定！