智能优化算法——布谷鸟搜索算法原理（附代码）

目录

基本概念

算法具体流程

   算法流程图

测试函数

优化结果

visual studio2017C++代码

基本概念

布谷鸟搜索算法（Cuckoo Search，缩写 CS）是由剑桥大学杨新社教授和S.戴布于2009年提出的一种新兴启发算法。根据昆虫学家的长期观察研究发现，一部分布谷鸟以寄生的方式养育幼鸟，它们不筑巢，而是将自己的卵产在其他鸟的巢中（通常为黄莺、云雀等），由其他鸟(义亲)代为孵化和育雏。然而，如果这些外来鸟蛋被宿主发现，宿主便会抛弃这些鸟蛋或新筑鸟巢。

通俗理解就是，布谷鸟蛋找到能成功在其他鸟巢成功孵化这个过程就是寻优过程。布谷鸟算法源于对布谷鸟繁育行为的模拟，为了简化自然界中布谷鸟的繁衍习性，Yang 等将布谷鸟的产卵行为假设为3个理想状态。

布谷鸟一次只产一个卵，并随机选择鸟窝位置来孵化它。
在随机选择的一组鸟窝中，最好的鸟窝将会被保留到下一代。
可选择的寄生巢的数量是固定的，寄生巢主人发现外来鸟蛋的概率为pa，其中 $0\leq pa\leqslant 1$ 。

基于这 3 个理想状态，Yang 等采用式（1）对下代鸟巢位置 $X_{i}^{t+1}$ 进行更新：

       $X_{i}^{t+1}=X_{i}^{t}+\alpha \bigotimes Levy(\lambda )$     (1)

式中： $X_{i}^{t}$ 表示第 $i(i=1,2,3,...,n)$ 个鸟巢在第t代的位置； $\bigotimes$ 表示点对点乘法； $\alpha$ 表示步长控制量，用来控制步长大小，通常情况下，取 $\alpha=1$ 。 $Levy(\lambda )$ 为Levy随机搜索路径，属于随机行走，采用莱维飞行机制，其行走的步长满足一个重尾的稳定分布，而随机步长为levy分布:

    $Levy:\mu =t^{-\lambda },1\leq \lambda \leqslant 3$                                          (2)

基本布谷鸟搜索算法先按照式（1）对下一代的鸟巢位置进行更新，并且计算目标函数的适应度值，如果该值优于上一代的目标函数值，则更新鸟巢位置，否则保持原来位置不变。通过位置更新后，用随机产生的服从 0 到 1 均匀分布的数值𝑅与鸟巢主人发现外来鸟蛋的概率pa相比较，若R>pa，则 $X_{i}^{t+1}$ 对进行随机改变，反之不变。最后保留测试值较好的一组鸟窝位置 $X_{i}^{t+1}$ ，记为 $X_{i}^{t+1}$ 。判断算法是否满足设置的最大迭代次数：若满足，结束迭代寻优，输出全局最优值fmin ；否则，继续迭代寻优。该算法具有全局探索和局部开发性能的平衡以及种群的多样性。

算法具体流程

Step 1（初始化）确定目标函数 $f(x),X=(x_{1},...,x_{d})^{T}$ 初始化群体，随机产生n个鸟窝的初始位置 $X_{i}(i=1,2,...,n)$ 。设置算法参数：种群规模N、维度D、发现概率pa、界值大小L、最大迭代次数MaxN、最优鸟窝位置 $X_{best}^{0}$ 和最优解 $f_{min}$ 。

Step 2（循环体）按式（1）、（2）更新当代鸟窝的位置；将当代鸟窝与上一代鸟窝位置 $P_{t-1}=\left [ X_{1}^{t-1} ,X_{2}^{t-1},...,X_{n}^{t-1} \right ]^{T}$ 进行对比,用适应度值较好的鸟窝位置替换适应度值较差的鸟窝位置： $g_{t}=\left [ X_{1}^{t} ,X_{2}^{t},...,X_{n}^{t} \right ]^{T}$ 。

Step 3（循环体）用随机数𝑅作为鸟窝主人发现外来鸟蛋的可能性，将其与鸟被淘汰的概率pa进行比较。若𝑅 >pa则随机改变 $g_{t}$ 中的鸟窝位置,得到一组新的鸟窝位置。再更新鸟窝位置，得到一组较好的鸟窝位置： $p_{t}=\left [ X_{1}^{t} ,X_{2}^{t},...,X_{n}^{t} \right ]^{T}$ 。更新最优鸟窝位置 $X_{best}^{t}$ 和最优解 $f^{t}_{min}$ 。

Step 4 判断算法是否满足设置的最大迭代次数：若满足，结束搜索过程，输出全局最优值 $f_{min}$ ，否则，重复step2进行迭代寻优。

算法流程图

测试函数

优化变量： $x_{1},x_{2}$

约束条件： $x_{low}=\left \{ -2,-2 \right \},x_{high}=\left \{ 2,2 \right \}$

目标函数: $f(x)=\left [ 1+(x_{1}+x_{2}+1)^{2} (19-14x_{1}+3x_{1}^{2}-14x_{2}+6x_{1}x_{2}+3x_{2}^{2})\right ]\times \left [ 30+(2x_{1}-3x_{2})^{2} (18-32x_{1}+12x_{1}^{2}+48x_{2}-36x_{1}x_{2}+27x_{2}^{2})\right ]$

式中， Goldstein-Price函数f(x)是一个二元八次多项式，作为常见的算法测试函数，许多科研人员利用它研究其局部最小值。上式为该优化问题的数学优化模型，该函数的理论结果为在(0,-1)处取得最小值3。

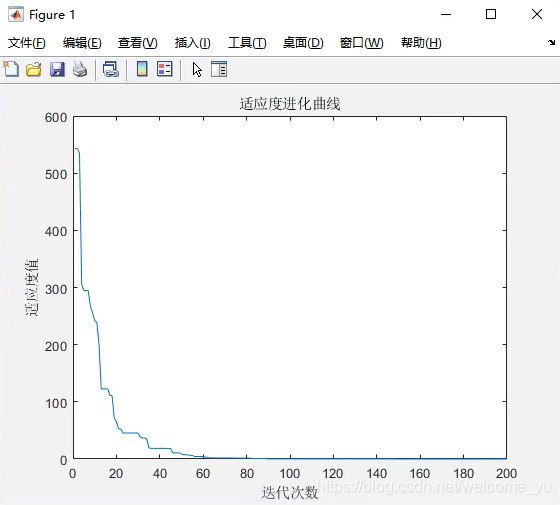
优化结果

从上图可以看出，布谷鸟搜索算法优化最小值为3.02573，迭代400次用时2.119s。

visual studio2017C++代码

头文件：

//布谷鸟搜索算法
//开发人员：chenshuai      开发日期：2019.11.25  邮箱：chenshuai0614@hrbeu.edu.cn 
//************************************************************************************//
//布谷鸟算法参数设定
//************************************************************************************//
#ifndef PCH_H
#define PCH_H
#include <iostream>
# include <fstream>
#include <iomanip>
#include <math.h>
#include <cstdlib> // 标准库
#include <ctime> // 时间库
#include <vector> //容器头文件
#include<random>
#define  PI    3.1415926535897    //π值
using namespace std;
//产生随机小数或整数
class RandomNumber {
public:RandomNumber() {srand((unsigned)time(NULL));    //析构函数，在对象创建时数据成员执行初始化操作}int integer(int begin, int end){return rand() % (end - begin + 1) + begin;}double decimal(double a, double b){return double(rand() % 10000) / 10000 * (b - a) + a;}
};
class cs {
private:int N_nest;//种群（布谷鸟巢总数）int Max_iteration;//最大迭代次数，int D_egg;//变量个数(布谷鸟蛋维数)double pa;//布谷鸟蛋被发现的概率double cs_alpha;//步长控制量double R;  //随机数R
public:double lambda;vector<double>fmin;                      //最优解vector<vector<double>>f_nest;            //鸟窝的适应度值vector<vector<double>>p_t;              //与上一代比较后最优的鸟窝种群vector<vector<double>>g_t;              //被发现之后，更新的最优鸟窝种群vector<double>nest_best;        //最好的鸟窝vector<double>nest_low = { -2,-2 };   //储存变量上限值  （鸟窝的上限）vector<double>nest_high = { 2,2 };   //储存变量下限值   （鸟窝的下限）//*******************************************////定义函数//*******************************************//void setParameters();//设置算法参数int N_nest,int Max_iteration,int D_egg,double cs_alphavoid initialize();                //初始化double select_optimal(vector<vector<double>>x);            //选择最优的鸟巢double fit_function(vector<double> x); //目标函数vector<vector<double>> update_Levyflight(vector<vector<double>>x, int t);//莱维飞行更新鸟窝位置vector<vector<double>> update_Rrandomnumber(vector<vector<double>>x);//随机数R更新鸟窝位置
};#endif //PCH_H

函数文件：

#include "pch.h"
//***********************************************
//设置布谷鸟算法参数
//**********************************************
void cs::setParameters()
{N_nest = 100; //种群（布谷鸟巢总数）Max_iteration = 400;//最大迭代次数，D_egg = 2;//变量个数(布谷鸟蛋维数)pa = 0.25;//布谷鸟蛋被发现的概率cs_alpha = 1.0;//步长控制量
}
//**********************************************
//初始化群体，N个鸟窝的初始位置
//**********************************************
void cs::initialize()
{extern RandomNumber r;       //定义随机数fmin.resize(Max_iteration);p_t.resize(N_nest, vector<double>(D_egg));g_t.resize(N_nest, vector<double>(D_egg));f_nest.resize(Max_iteration, vector<double>(N_nest));nest_best.resize(D_egg);for (int i = 0; i < N_nest; i++){for (int j = 0; j < D_egg; j++){p_t[i][j] = r.decimal(nest_low[j], nest_high[j]);//初始化鸟窝的值}}
}
//***********************************************
//鸟窝位置的适应度
//**********************************************
double cs::fit_function(vector<double>x)
{double fx = 0;//Rastrigin函数/*for (int i = 0; i < 2; i++){fx = fx + x[i] * x[i] - 10 * cos(2 * PI*x[i]) + 10;}*///Goldstein	-Price函数fx = (1 + pow((1 + x[0] + x[1]), 2)*(19 - 14 * x[0] + 3 * x[0] * x[0] - 14 * x[1] + 6 * x[0] * x[1] + 3 * x[1] * x[1]))*(30 + pow((2 * x[0] - 3 * x[1]), 2)*(18 - 32 * x[0] + 12 * x[0] * x[0] + 48 * x[1] - 36 * x[0] * x[1] + 27 * x[1] * x[1]));//SiX-Hump Camel函数//fx = 4 * x[0] * x[0] - 2.1*pow(x[0], 4) + 1.0 / 3.0*pow(x[0], 6) + x[0] * x[1] - 4 * x[1] * x[1] + 4 * pow(x[1], 4);return fx;
}
//**********************************************
//计算每个鸟窝的目标函数值并记录当前的最优解
//**********************************************
double cs::select_optimal(vector<vector<double>>x)
{double fmin = 0;fmin = fit_function(x[0]);for (int i = 1; i < N_nest; i++){if (fmin > fit_function(x[i])){fmin = fit_function(x[i]);for (int j = 0; j < D_egg; j++){nest_best[j] = x[i][j];}}}return fmin;
}
//**********************************************
//随机数R更新鸟窝位置
//**********************************************
vector<vector<double>> cs::update_Rrandomnumber(vector<vector<double>>x)
{extern RandomNumber r;       //声明全局随机数for (int j = 0; j < N_nest; j++){for (int k = 0; k < D_egg; k++){R = r.decimal(0, 1);if (R > pa){x[j][k] = r.decimal(nest_low[k], nest_high[k]);}}}return x;
}
//**********************************************
//莱维飞行更新每个鸟窝的位置
//**********************************************
vector<vector<double>> cs::update_Levyflight(vector<vector<double>>x, int t)
{extern RandomNumber r;       //声明全局随机数for (int j = 0; j < N_nest; j++){for (int k = 0; k < D_egg; k++){lambda = r.decimal(1, 3);x[j][k] = x[j][k] + cs_alpha * pow(t, -1 * lambda);if (x[j][k]< nest_low[k] || x[j][k] > nest_high[k]){x[j][k] = r.decimal(nest_low[k], nest_high[k]);}}}return x;
}

主函数：

#include "pch.h"
#include <iostream>
RandomNumber r;       //随机数
int main()
{clock_t startTime, endTime; //定义程序开始运行时间和结束时间startTime = clock();  //计时开始cs CS;          //定义布谷鸟种群CS.setParameters();//设置算法参数CS.initialize(); //初始化CS.fmin[0] = CS.select_optimal(CS.p_t);//选择初代最优个体cout << CS.fmin[0] << endl;//循环体ofstream out("布谷鸟算法优化结果.txt");for (int i = 1; i < size(CS.fmin); i++){CS.p_t = CS.update_Levyflight(CS.p_t, i);  //莱维飞行更新鸟窝的位置CS.fmin[i] = CS.select_optimal(CS.p_t);if (CS.fmin[i] > CS.fmin[i - 1]){CS.fmin[i] = CS.fmin[i - 1];}CS.p_t = CS.update_Rrandomnumber(CS.p_t);//随机数R发现更新鸟窝的位置if (CS.fmin[i] > CS.select_optimal(CS.p_t)){CS.fmin[i] = CS.select_optimal(CS.p_t);}out << i << fixed << setw(12) << setprecision(5) << CS.fmin[i] << endl;}out << "最优变量:" << endl;for (int ii = 0; ii < size(CS.nest_best); ii++){out << "x" << ii << "=" << fixed << setw(12) << setprecision(5) << CS.nest_best[ii] << endl;//输出最优变量}out << "最优值=" << fixed << setw(12) << setprecision(5) << CS.fmin[size(CS.fmin) - 1] << endl;endTime = clock();//计时结束out << "run time:" << (double)(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
}

各位阅读文章的朋友觉得文章可以给个好评或者点赞，大家觉得有问题可以指出来或者发邮箱chenshuai0614@hrbeu.edu.cn联系我！如需要转载请附上链接，谢谢各位朋友！