Written: Understanding word2vec

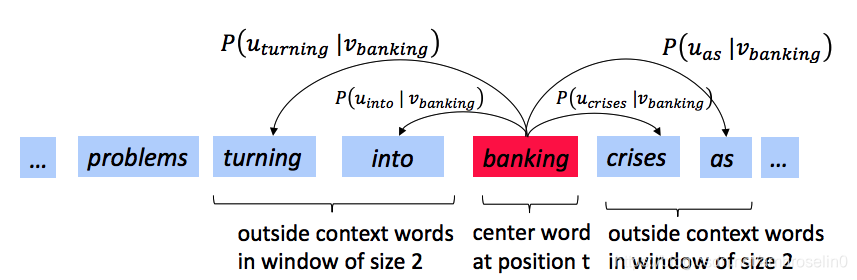
Let’s have a quick refresher on the word2vec algorithm. The key insight behind word2vec is that ‘a word is known by the company it keeps’. Concretely, suppose we have a ‘center’ word $c$ and a contextual window surrounding $c$. We shall refer to words that lie in this contextual window as ‘outside words’. For example, in Figure 1 we see that the center word c is ‘banking’. Since the context window size is 2, the outside words are ‘turning’, ‘into’, ‘crises’, and ‘as’.

The goal of the skip-gram word2vec algorithm is to accurately learn the probability distribution $P(O|C)$. Given a specific word $o$ and a specific word $c$, we want to calculate $P(O=o|C=c)$, which is the probability that word $o$ is an ‘outside’ word for $c$, i.e., the probability that $o$ falls within the contextual window of $c$.

In word2vec, the conditional probability distribution is given by taking vector dot-products and applying the softmax function:
$$P(O=o|C=c)=\frac{\exp ({{\mathbf{u}}_{\mathbf{o}}}^{\top }{v}_c)}{{\sum }_{w\in Vocab}\exp ({{\mathbf{u}}_{\mathbf{w}}}^{\top }{v}_c)}\text{\hspace{1em}(1)}$$

Here, $u_o$ is the ‘outside’ vector representing outside word $o$, and $v_c$ is the ‘center’ vector representing center word $c$. To contain these parameters, we have two matrices, $U$ and $V$ . The columns of $U$ are all the ‘outside’ vectors $u_w$ . The columns of $V$ are all of the ‘center’ vectors $v_w$ . Both $U$ and $V$ contain a vector for every $w\in$ Vocabulary.¹

Recall from lectures that, for a single pair of words $c$ and $o$, the loss is given by:
$$J_{naive-softmax}(v_c,o,U)=-\log P(O=o|C=c)\text{\hspace{1em}(2)}$$
Another way to view this loss is as the cross-entropy² between the true distribution y and the predicted distribution $\hat{y}$. Here, both $y$ and $\hat{y}$ are vectors with length equal to the number of words in the vocabulary. Furthermore, the $k^{th}$ entry in these vectors indicates the conditional probability of the $k^{th}$ word being an ‘outside word’ for the given $c$. The true empirical distribution $y$ is a one-hot vector with a 1 for the true outside word $o$, and 0 everywhere else. The predicted distribution $\hat{y}$ is the probability distribution $P(O|C=c)$ given by our model in equation (1).

Question a

Show that the naive-softmax loss given in Equation (2) is the same as the cross-entropy loss between $y$ and $\hat{y}$; i.e., show that

$$-\sum _{w\in Vocab}{y}_w\log ({\hat{y}}_w)=-\log ({\hat{y}}_o)\text{\hspace{1em}(3)}$$

Ans for a

$$y_w=\{\begin{array}{r}1,w=o\\ 0,w̸=o\end{array}$$

$$-\sum _{w\in Vocab}{y}_w\log ({\hat{y}}_w)=-y_o\log (\widehat{y_o})=-\log (\widehat{y_o})$$

Question b

Compute the partial derivative of $J_{naive-softmax}(v_c,o,U)$ with respect to $v_c$. Please write your answer in terms of $y$, $\hat{y}$, and $U$.

Ans for b

$$\begin{array}{rl}\frac{\partial }{\partial v_c}{J}_{naive-softmax}=& -\frac{\partial }{\partial v_c}\log P(O=o|C=c)\\ =& -\frac{\partial }{\partial v_c}\log \frac{\exp (u_o^T{v}_c)}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}\\ =& -\frac{\partial }{\partial v_c}\log \exp (u_o^T{v}_c)+\frac{\partial }{\partial v_c}\log \sum _{w=1}^V\exp (u_w^T{v}_c)\\ =& -u_o+\frac{1}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}\frac{\partial }{\partial v_c}\sum _{x=1}^V\exp (u_x^T{v}_c)\\ =& -u_o+\frac{1}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}\sum _{x=1}^V\exp (u_x^T{v}_c)\frac{\partial }{\partial v_c}{u}_x^T{v}_c\\ =& -u_o+\frac{1}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}\sum _{x=1}^V\exp (u_x^T{v}_c)u_x\\ =& -u_o+\sum _{x=1}^V\frac{\exp (u_x^T{v}_c)}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}{u}_x\\ =& -u_o+\sum _{x=1}^{V}P(O=x|C=c)u_x\\ =& -y^T{U}^T+{\hat{y}}^T{u}^T\\ =& U(\hat{y}-y)\end{array}$$

Question c

Compute the partial derivatives of $J_{naive-softmax}(v_c,o,U)$ with respect to each of the ‘outside’ word vectors, $u_w$'s. There will be two cases: when $w=o$, the true ‘outside’ word vector, and $w̸=o$, for all other words. Please write you answer in terms of $y$, $\hat{y}$, and $v_c$.

Ans for c

$$\begin{array}{rl}\frac{\partial }{\partial u_w}{J}_{naive-softmax}=& -\frac{\partial }{\partial u_w}\log \frac{\exp (u_o^T{v}_c)}{{\sum }_{m=1}^V\exp (u_m^T{v}_c)}\\ =& -\frac{\partial }{\partial u_w}\log \exp (u_o^T{v}_c)+\frac{\partial }{\partial u_w}\log \sum _{m=1}^V\exp (u_m^T{v}_c)\end{array}$$

When $w=o$:

$$\begin{array}{rl}\frac{\partial }{\partial u_o}{J}_{naive-softmax}=& -v_c+\frac{1}{{\sum }_{m=1}^V\exp (u_m^T)}\sum _{n=1}^V\frac{\partial }{\partial u_o}\exp (u_n^T{v}_c)\\ =& -v_c+\frac{1}{{\sum }_{m=1}^V\exp (u_m^T)}\frac{\partial }{\partial u_o}\exp (u_o^T{v}_c)\\ =& -v_c+\frac{\exp (u_o^T{v}_c)}{{\sum }_{m=1}^V\exp (u_m^T)}{v}_c\\ =& -v_c+P(O=o|C=c)v_c\\ =& (P(O=o|C=c)-1)v_c\end{array}$$

When $w̸=o$:

$$\begin{array}{rl}\frac{\partial }{\partial u_w}{J}_{naive-softmax}=& \frac{\partial }{\partial u_w}\log \sum _{m=1}^V\exp (u_m^T{v}_c)\\ =& \frac{\exp (u_w^T{v}_c)}{{\sum }_{m=1}^V\exp (u_m^T)}{v}_c\\ =& P(O=w|C=c)v_c\\ =& (P(O=o|C=c)-0)v_c\end{array}$$

In summary:

$$\begin{array}{rl}\frac{\partial }{\partial u_w}{J}_{naive-softmax}=& ({\hat{y}}_w-y_w)v_c\end{array}$$

Question d

The sigmoid function is given by Equation 4:
$$\sigma (x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}\text{\hspace{1em}(4)}$$
Please compute the derivative of $\sigma (x)$ with respect to $x$, where $x$ is a vector.

Ans for d

$$\begin{array}{rl}\frac{\partial }{\partial x}\sigma (x)=& \frac{\partial }{\partial x}\frac{e^x}{e^x+1}\\ =& \frac{\partial }{\partial y}\frac{y}{y+1}\frac{\partial }{\partial x}{e}^x\\ =& \frac{\partial }{\partial y}(1-\frac{1}{y+1})\frac{\partial }{\partial x}{e}^x\\ =& \frac{\partial }{\partial y}\frac{1}{y+1}\frac{\partial }{\partial x}{e}^x\\ =& \frac{1}{y+1}\frac{\partial }{\partial x}{e}^x\\ =& \frac{e^x}{(e^x+1{)}^2}\\ =& \frac{e^x}{e^x+1}\frac{1}{e^x+1}\\ =& \frac{e^x}{e^x+1}\frac{e^x+1-e^x}{e^x+1}\\ =& \frac{e^x}{e^x+1}(1-\frac{e^x}{e^x+1})\\ =& \sigma (x)(1-\sigma (x))\end{array}$$

Question e

Now we shall consider the Negative Sampling loss, which is an alternative to the Naive Softmax loss. Assume that $K$ negative samples (words) are drawn from the vocabulary. For simplicity of notation we shall refer to them as $w_1,w_2,\dots ,w_K$ and their outside vectors as $u_1,\dots ,u_K$. Note that$ o\notin {w_1,…,w_K}$. For a center word $c$ and an outside word $o$, the negative sampling loss function is given by:
$$J_{neg-sample}(v_c,o,U)=-\log (\sigma ({{\mathbf{u}}_{\mathbf{o}}}^{\top }{v}_c))-\sum _{K=1}^K\log (\sigma (-{{\mathbf{u}}_{\mathbf{k}}}^{\top }{v}_c))\text{\hspace{1em}(5)}$$
for a sample $w_1,...w_K$ , where $\sigma (\cdot )$ is the sigmoid function³

Please repeat parts (b) and ©, computing the partial derivatives of $J_{neg-sample}$ with respect to $v_c$, with respect to $u_o$, and with respect to a negative sample $u_k$. Please write your answers in terms of the vectors $u_o$, $v_c$, and $u_k$, where $k\in [1,K]$. After you’ve done this, describe with one sentence why this loss function is much more efficient to compute than the naive-softmax loss. Note, you should be able to use your solution to part (d) to help compute the necessary gradients here.

Ans for e

$$\begin{array}{rl}\frac{\partial }{\partial v_c}{J}_{neg-sample}=& -\frac{\partial }{\partial v_c}\log (\sigma (u_o^T{v}_c))-\frac{\partial }{\partial v_c}\sum _{k=1}^K\log (\sigma (-u_k^T{v}_c))\\ =& -\frac{1}{\sigma (u_o^T{v}_c)}\frac{\partial }{\partial v_c}\sigma (u_o^T{v}_c)-\sum _{k=1}^K\frac{1}{\sigma (-u_k^T{v}_c)}\frac{\partial }{\partial v_c}\sigma (-u_k^T{v}_c)\\ =& -\frac{1}{\sigma (u_o^T{v}_c)}\sigma (u_o^T{v}_c)(1-\sigma (u_o^T{v}_c))\frac{\partial }{\partial v_c}{u}_o^T{v}_c-\sum _{k=1}^K\frac{1}{\sigma (-u_k^T{v}_c)}\sigma (-u_k^T{v}_c)(1-\sigma (u_k^T{v}_c))\frac{\partial }{\partial v_c}(-u_k^T{v}_c)\\ =& (\sigma (u_o^T{v}_c)-1)u_o-\sum _{k=1}^K(\sigma (-u_k^T{v}_c)-1)u_k\\ & \\ \frac{\partial }{\partial u_o}{J}_{neg-sample}=& -\frac{\partial }{\partial u_o}\log (\sigma (u_o^T{v}_c))-\frac{\partial }{\partial u_o}\sum _{k=1}^K\log (\sigma (-u_k^T{v}_c))\\ =& -\frac{\partial }{\partial u_o}\log (\sigma (u_o^T{v}_c))\\ =& -\frac{1}{\sigma (u_o^T{v}_c)}\frac{\partial }{\partial u_o}\sigma (u_o^T{v}_c)\\ =& -\frac{1}{\sigma (u_o^T{v}_c)}\sigma (u_o^T{v}_c)(1-\sigma (u_o^T{v}_c))\frac{\partial }{\partial u_o}{u}_o^T{v}_c\\ =& (\sigma (u_o^T{v}_c)-1)v_c\\ & \\ \frac{\partial }{\partial u_k}{J}_{neg-sample}=& -\frac{\partial }{\partial u_k}\log (\sigma (u_o^T{v}_c))-\frac{\partial }{\partial u_k}\sum _{x=1}^K\log (\sigma (-u_x^T{v}_c))\\ =& -\frac{\partial }{\partial u_k}\sum _{x=1}^K\log (\sigma (-u_x^T{v}_c))\\ =& -\frac{\partial }{\partial u_k}\log (\sigma (-u_k^T{v}_c))\\ =& -\frac{1}{\sigma (-u_k^T{v}_c)}\frac{\partial }{\partial u_k}\sigma (-u_k^T{v}_c)\\ =& -\frac{1}{\sigma (-u_k^T{v}_c)}\sigma (-u_k^T{v}_c)(1-\sigma (-u_k^T{v}_c))\frac{\partial }{\partial u_k}(-u_k^T{v}_c)\\ =& (1-\sigma (-u_k^T{v}_c))v_c\end{array}$$

Cause through this loss funtion, we don’t need to go through all word in vocabulary which cost expensive.

Question f

Suppose the center word is $c=w_t$ and the context window is $[w_{t-m},...,w_{t-1},w_t,w_{t+1},...,w_{t+m}]$, where $m$ is the context window size. Recall that for the skip-gram version of word2vec, the total loss for the context window is:
$$J_{skip-gram}(v_c,w_{t-m},...w_{t+m},U)=\sum _{-m\le j\le m,j̸=0}J(v_c,wt+j,U)\text{\hspace{1em}(6)}$$
Here, $J(v_c,w_{t+j},U)$ represents an arbitrary loss term for the center word $c=w_t$ and outside word $w_{t+j}$. $J(v_c,w_{t+j},U)$ could be $J_{naive-softmax}(v_c,w_{t+j},U)$ or $J_{neg-sample}(v_c,w_{t+j},U)$, depending on your implementation.

Write down three partial derivatives:

1. $\frac{\partial J_{skip-gram}(v_c,w_{t-m},\dots w_{t+m},U)}{\partial U}$
2. $\frac{\partial J_{skip-gram(v_c,w_{t-m,\dots w_{t+m},U})}}{\partial v_c}$
3. $\frac{\partial J_{skip-gram(v_c,w_{t-m},\dots w_{t+m},U)}}{\partial v_w}$ when $w̸=c$

Write your answers in terms of $\frac{\partial J(v_c,w_{t+j},U)}{\partial U}$ and $\frac{\partial J(v_c,w_{t+j},U)}{\partial v_c}$. This is very simple - each solution should be one line.

Ans for f

$$\begin{array}{rl}\frac{\partial }{\partial U}{J}_{skip-gram}(v_c,w_{t-m},\dots w_{t+m},U)=& \sum _{-m\le j\le m}\frac{J(v_c,w_{t+j},U)}{\partial U}\\ & \\ \frac{\partial }{\partial v_c}{J}_{skip-gram(v_c,w_{t-m,\dots w_{t+m},U})}=& \sum _{-m\le j\le m}\frac{J(v_c,w_{t+j},U)}{\partial v_c}\\ & \\ \frac{\partial }{\partial v_w}{J}_{skip-gram(v_c,w_{t-m},\dots w_{t+m},U)}=& 0\end{array}$$

---

1. Assume that every word in our vocabulary is matched to an integer number $k.u_k$ is both the $k^{th}$ column of $U$ and the ‘outside’ word vector for the word indexed by $k.v_k$ is both the $k^{th}$ column of $V$ and the ‘center’ word vector for the word indexed by $k$. In order to simplify notation we shall interchangeably use $k$ to refer to the word and the index-of-the-word. ↩︎

2. The Cross Entropy Loss between the true (discrete) probability distribution $p$ and another distribution $q$ is$ − \sum_{i}p_i log(q_i)$. ↩︎

3. Note: the loss function here is the negative of what Mikolov et al. had in their original paper, because we are doing aminimization instead of maximization in our assignment code. Ultimately, this is the same objective function. ↩︎