一、理论基础

1、算法原理

布谷鸟采用一种特殊的寄生宿主巢穴的方式孕育繁殖,它将孵育的蛋置入寄生宿主的巢穴，让寄生宿主孵化布谷鸟蛋。由于布谷鸟幼雏能发出比寄生宿主幼雏更闪亮的叫声，因此获得更多的食物，具有更高的存活率。在某些情形下，寄生宿主发现巢穴内不是宿主幼雏，则会遗弃该巢穴，并重新选择新的巢穴孵育繁殖。Yang X. S.和Deb等人基于上述孵育寄生机理，提出布谷鸟搜索算法。它遵循以下3个理想规则。
规则1. 每只布谷鸟1次有且仅有孵化1个蛋，并随机选择1个寄生宿主巢穴存放。
规则2. 在随机选择的1个寄生宿主巢穴中，最优的寄生宿主巢穴将被保留至下一代。
规则3. 可利用的寄生宿主巢穴数量是固定的，1个寄生宿主巢穴的宿主发现寄生布谷鸟蛋的概率为$P_a$。
基于上述3个理想规则，可以得到1个宿主巢穴代表1个候选解。因此，布谷鸟算法的基本算法流程包含3部分：首先，在当前候选解的基础上，以Levy飞行随机游动生成新的候选解，评价并保留较好的候选解；其次，按照发现概率$P_a$舍弃部分候选解；最后，按照偏好随机游动方式产生新的候选解并替代舍弃的解，保留较好解后进入下一次进化，直至满足算法的收敛条件。
设布谷鸟算法进化至第$r$代时第$m$个候选解为${\mathbf{X}}_{r,m}$，${\mathbf{X}}_{r,m}=(x_{r,m}^{(1)},x_{r,m}^{(2)},\cdots ,x_{r,m}^{(j)},\cdots ,x_{r,m}^{(D)}),j\in [1,D]$。采用Levy飞行随机游动产生新的个体(候选解)${\mathbf{X}}_{r+1,m}$更新的表达式为$${\mathbf{X}}_{r+1,m}={\mathbf{X}}_{r,m}+({\mathbf{X}}_{r,m}-{\mathbf{X}}_{r,gb})\cdot ({\gamma }_0\oplus L(\beta ))\text{\hspace{1em}(1)}$$其中，${\mathbf{X}}_{r,gb}$为当前搜索到的全局最优解，$L(\beta )$表示Levy飞行随机游动的路径，${\gamma }_0$表示初始搜索步长，$\oplus$表示点对点乘法，$t$为飞行时间：$$L(\beta )\sim \vartheta =t^{-1-\beta },0<\beta \le 2\text{\hspace{1em}(2)}$$通过数学代换，式(2)等价于：$$L(\beta )\sim \frac{\vartheta }{|\nu {|}^{1/\beta }}{\left(\frac{\Gamma (1+\beta )sin(\pi \cdot \beta /2)}{\Gamma \left(\frac{1+\beta }{2}\right)\cdot \beta \cdot 2^{(\beta -1)/2}}\right)}^{1/\beta }\text{\hspace{1em}(3)}$$其中，$\Gamma (\cdot )$为伽马函数，取$\beta =1.5$；$\vartheta ,\nu$为标准高斯分布随机数。
在偏好随机游动方式中，按照发现概率$P_a$舍弃部分候选解后，生成相同数量的新解：$${\mathbf{X}}_{r+1,m}={\mathbf{X}}_{r,m}+\varphi \cdot ({\mathbf{X}}_{r,k}-{\mathbf{X}}_{r,s})\text{\hspace{1em}(4)}$$其中，$\varphi$为算法的控制缩放系数，满足$\varphi \in U(0,1)$；${\mathbf{X}}_{r,k}$和${\mathbf{X}}_{r,s}$分别为第$r$代时第$k$个和第$s$个随机候选解。

2、算法流程图

根据以上分析，布谷鸟搜索算法流程图如图1所示。

图1 布谷鸟搜索算法流程图

二、Matlab代码

以Sphere函数为目标函数，种群规模$N=30$，发现概率$P_a=0.25$，维数$dim=30$，上下限为$[-100,100]$，最大迭代次数$Max\_iter=1000$。完整程序如下：

%% 清除环境变量
clear;
clc;%% CS参数
% 种群规模(鸟巢数量)
N = 30;
% 发现概率
pa = 0.25;Max_iter = 1000;     % 最大迭代次数
% 边界
dim = 30;                     % 维数
Lb = -100*ones(1, dim);    % 下限
Ub = 100*ones(1, dim);     % 上限% 随机初始化种群位置
for i = 1:Nnest(i, :) = Lb+(Ub-Lb).*rand(1, dim);
end
% 初始最优解
fitness = 10^10*ones(N, 1);
[fmin, bestnest, nest, fitness] = get_best_nest(nest, nest, fitness);% N_iter = 0;
%% 迭代寻优
for iter = 1:Max_iter%% 通过莱维飞行得到新个体beta = 3/2;sigma = (gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);for i = 1:Ns = nest(i, :);% 用蒙特卡洛方法模拟莱维飞行u = randn(size(s))*sigma;v = randn(size(s));step = u./abs(v).^(1/beta);stepsize = 0.01*step.*(s-bestnest);s=s+stepsize.*randn(size(s));% 边界处理new_nest(i, :) = simplebounds(s, Lb, Ub);end% 新个体和旧个体适应度值贪婪比较，选取最优个体[fnew, best, nest, fitness] = get_best_nest(nest, new_nest, fitness);%      % 更新计数器%      N_iter = N_iter+N;% 发现和随机化new_nest = empty_nests(nest, Lb, Ub, pa) ;% 新个体和旧个体适应度值贪婪比较，选取最优个体[fnew, best, nest, fitness] = get_best_nest(nest, new_nest, fitness);%      % 再次更新计数器%      N_iter = N_iter+N;% 更新全局最优解if fnew < fminfmin = fnew;bestnest = best;end%% 记录每代最优解Curve(iter) = fmin;%% 显示每代优化结果display(['CS:At iteration ', num2str(iter), ' the best fitness is ', num2str(fmin)]);
end%% Display all the nests
% disp(strcat('Total number of iterations=', num2str(N_iter)));
%% 最终结果显示
disp(['最终位置：' , num2str(bestnest)]);
disp(['最终函数值：', num2str(Curve(end))]);
%% 绘图
figure;
plot(Curve, 'r', 'lineWidth', 2);          %  画出迭代图
xlabel('迭代次数', 'fontsize', 12);
ylabel('目标函数值', 'fontsize', 12);%% ---------------下面列出了所有子函数------------------
%% 发现最优位置
function [fmin, best, nest, fitness] = get_best_nest(nest, newnest, fitness)
for j = 1:size(nest,1)fnew = fobj(newnest(j,:));if fnew <= fitness(j)fitness(j) = fnew;nest(j, :) = newnest(j, :);end
end
% Find the current best
[fmin, K] = min(fitness) ;
best = nest(K, :);
end
%% 通过构造新的个体来替代某些个体
function new_nest = empty_nests(nest, Lb, Ub, pa)
% 一小部分更糟的巢穴被发现的概率为pa
n = size(nest, 1);
% 发现与否——一个状态向量
K = rand(size(nest)) > pa;% 有偏/选择随机游动的新解
stepsize = rand*(nest(randperm(n), :)-nest(randperm(n), :));
new_nest = nest+stepsize.*K;
for j = 1:size(new_nest, 1)s = new_nest(j, :);new_nest(j, :) = simplebounds(s, Lb, Ub);
end
end%% 边界处理
function s = simplebounds(s,Lb,Ub)
% Apply the lower bound
ns_tmp = s;
I = ns_tmp<Lb;
ns_tmp(I) = Lb(I);% Apply the upper bounds
J = ns_tmp>Ub;
ns_tmp(J) = Ub(J);
% Update this new move
s = ns_tmp;
end%% 目标函数
function z = fobj(u)
z=sum(u.^2);
end

最终位置和最优目标函数值为：

最终位置：0.021557    0.013997  -0.0038913   -0.013907  -0.0087341  -0.0013441  -0.0057873 -0.00091699 -0.00034563  -0.0085162   0.0015167   -0.018136  -0.0040665   -0.023025  -0.0067345  -0.0085958   0.0082373    -0.02232   0.0056112  -0.0089819  -0.0025091    0.013316  0.00094574 -0.00045218    0.012714   -0.011097    0.012178    0.012474    0.010687  -0.0091615
最终函数值：0.0037011

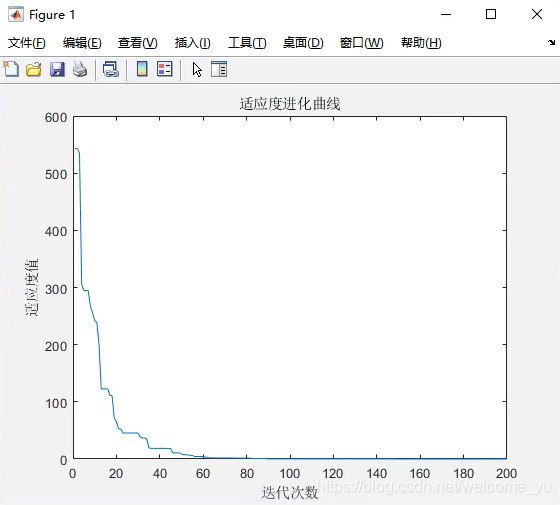
进化曲线如图2所示。

图2 CS算法进化曲线

三、参考文献

[1] Yang X S, Deb S. Engineering Optimisation by Cuckoo Search[J]. International Journal of Mathematical Modelling & Numerical Optimisation, 2010, 1(4): 330-343.
[2] 刘晓东, 孙丽君, 陈天飞. 布谷鸟算法的收敛性分析及性能比较[J]. 计算机科学与探索, 2020, 14(10): 1644-1655.
[3] 傅文渊. 具有万有引力加速机理的布谷鸟搜索算法[J]. 软件学报, 2021, 32(5): 1480-1494.