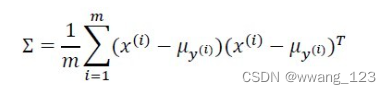布谷鸟搜索算法

布谷鸟搜索（Cuckoo Search，缩写 CS），也叫杜鹃搜索，是由剑桥大学杨新社（音译自：Xin-She Yang）教授和S.戴布（S.Deb）于2009年提出的一种新兴启发算法。

1.定义

CS算法是通过模拟某些种属布谷鸟的寄生育雏（BroodParasitism），来有效地求解最优化问题的算法。同时，CS也采用相关的Levy飞行搜索机制。

2.算法

（1）使用布谷鸟搜索算法的三个理想规则

a.每只布谷鸟一次只下一个蛋，然后把蛋放进随机选择的鸟巢里；（Each cuckoo lays one egg at a time, and dumps it in a randomly chosen nest）

b.在随机选择的鸟巢中，最好的鸟巢将被保留到下一代；（The best nests with high-quality eggs will be carried over to the next generations）

c.可用的寄主巢的数量是固定的，而且布谷鸟产卵的概率是由寄主鸟发现的。在这种情况下，宿主鸟要么扔掉蛋，要么干脆放弃鸟巢，建造一个全新的鸟巢。(The number of available host nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability . In this case, the host bird can either get rid of the egg, or simply abandon the nest and build a completely new nest)

从实现的角度来看，我们可以使用以下简单的表示法，即巢穴中的每个蛋代表一个解决方案，而每个布谷鸟只能产一个蛋（因此代表一个解决方案），目的是使用新的和潜在更好的解决方案（布谷鸟）来替换巢穴中不太好的解决方案。显然，该算法可以扩展到更复杂的情况，即每个嵌套有多个表示一组解的蛋。在目前的介绍中，我们将使用最简单的方法，即每个巢只有一个蛋。在这种情况下，蛋、巢或布谷鸟之间没有区别，因为每个巢对应一个蛋，也代表一只布谷鸟。

（2）算法相关参数

该算法采用局部随机游走和全局探索性随机游走的平衡组合，由切换参数控制。

局部随机游走可以写成：

（1）

其中， $x_{j}^{t}$ 和 $x_{k}^{t}$ 是通过随机置换随机选择的两个解， $H_{u}$ 是Heaviside函数， $\epsilon$ 是从均匀分布中提取的随机数， $s$ 是步长。⊗是一种新的运算符（点乘）。

另一方面，全局探索性随机游走是通过Levy飞行实现的：

而，

其中，这里 $\alpha >0$ 是步长比例因子，它应该与感兴趣问题的规模相关。在大多数情况下，我们可以使用α=O（L/10），L是感兴趣问题的特征量表，而在某些情况下，α=O（L/100）可以更有效，避免飞得太远。上述方程本质上是随机行动的随机方程。一般来说，随机游走是一个马尔可夫链，其下一个状态/位置仅取决于当前位置（上述等式中的第一项）和转移概率（第二项）。

附：Levy Flight的简单代码实现

>> clc;
clear;
x = [0,0];
y = [0,0];
beta = 3/2;
alpha_u = (gamma(1+beta)*sin(pi*beta/2)/(gamma(((1+beta)/2)*beta*2^((beta-1)/2))))^(1/beta);
alpha_v = 1;
for i=1:1000 u=normrnd(0,alpha_u,1);v=normrnd(0,alpha_v,1);s = u/(abs(v))^(1/beta);x(:,1) = x(:,2);x(:,2) = x(:,1)+1*s;u=normrnd(0,alpha_u,1);v=normrnd(0,alpha_v,1);s = u/(abs(v))^(1/beta);y(:,1) = y(:,2);y(:,2) = y(:,1)+1*s;plot(x,y);hold on;
end
axis square;

3.特点

a.满足全局收敛性；

b.布谷鸟搜索有两种搜索能力：局部搜索和全局搜索，由切换/发现概率控制。局部搜索非常密集，大约占搜索时间的1/4，而全局搜索大约占总搜索时间的3/4。这使得搜索空间可以在全局范围内得到更有效的探索，从而以更高的概率找到全局最优性。

4.算法步骤

步骤1：设置鸟巢的个数为n，搜索空间的维数为d，初始化鸟巢的位置 $p_{0}=[x_{1}^{(0)},x_{2}^{(0)}...x_{n}^{(0)},]^{T}$ ，并找出最优鸟巢的位置 $x_{b}^{(0)}$ ， $b\epsilon [1,2,...,n]$ 和最优解 $f_{min}$ ；

步骤2：循环体

（1）保留上代最优鸟巢的位置 $x_{b}^{t-1}$ ， $t$ 为整数，并利用(1)式更新其他鸟巢的位置；

（2）利用Levy Flight得到一组新的鸟巢的位置 $p_{t}=[x_{1}^{(t)},x_{2}^{(t)},...,x_{n}^{(t)}]^{T}$ ；

（3）与上一组产生的鸟巢位置 $p_{t-1}=[x_{1}^{t-1},x_{2}^{t-1},...,x_{n}^{t-1}]^{T}$ 进行对比，用适应值较好的鸟巢位置替换适应值较差的鸟巢位置，从而得到一组较优的鸟巢位置 $g_{t}=[x_{1}^{(t)},x_{2}^{(t)},...,x_{n}^{(t)},]^{T}$ ;

（4）通过位置更新后，用随机数 $\gamma =[0,1]$ 与宿主鸟发现外来鸟蛋的概率是 $p_{\alpha }$ （ $p_{\alpha }$ 一般设置为0.25）进行对比,若 $\gamma >p_{\alpha }$ ,则对 $x_{t}^{t+1}$ 的位置进行随机改变。保留 $g_{t}$ 中发现概率较小的鸟蛋的位置，并随机改变发现概率较大的鸟巢的位置，得到一组新的鸟巢的位置，与 $g_{t}$ 中鸟巢的位置进行对，用测试值较好的鸟巢位置代替测试值较差的鸟巢位置，得到一组较优的鸟巢位置 $p_{t}=[x_{1}^{(\omega)},x_{2}^{(\omega)},...,x_{n}^{(\omega)}]^{T}$ ；

步骤3：找出步骤2中最后得到的 $p_{t}$ 中的最优鸟巢位置 $x_{b}^{(t)}$ 和最优值 $f_{min}$ ，若达到迭代条件（规定的迭代次数或要求的精度）则输出全局最优值 $f_{min}$ 和全局最优位置 $x_{b}^{(t)}$ ，反之，返回步骤2继续迭代更新。

附.布谷鸟算法Java实现（别人写的）

package com.gxx.matrix;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;/*** 布谷鸟算法* 原理是，使用多个 散列函数，通过计算放到 表 中，当其中一个散列函数计算到的对应位置为空，则放入，* 当都不为空就进行一层层替换，达到一定次数后还是插入不了，则进行扩容，或者重新散列*/
public class Cuckoo {private String [] array ;//表private static final int DEFAULTSIZE = 7;private int  size ;private int reHash =0;private int tryCount = 33;List<HashAlgorithm>  hashAlgorithmList = new ArrayList<HashAlgorithm>();{//初始2个散列函数。hashAlgorithmList.add(new HashAlgorithm(17));hashAlgorithmList.add(new HashAlgorithm(23));}void remove(String key){if (key == null) {return;}for (HashAlgorithm hashAlgorithm : hashAlgorithmList) {//遍历算法集合 计算index值，int hashCode = hashAlgorithm.hashCode(key);int index = getIndex(hashCode);if (array[index]!=null && array[index].equals(key)) {array[index] = null;size--;}}}void insert(String key){while(true){for (int i = 0; i < tryCount; i++) {for (HashAlgorithm hashAlgorithm : hashAlgorithmList) {//遍历算法集合 计算index值，int hashCode = hashAlgorithm.hashCode(key);int index = getIndex(hashCode);if (array[index] == null ) {array[index] = key;//当表中索引无值，将元素放到表中size++;return;}}//执行到这说明 算法集合计算的index全部有值 进行替换操作int hashAlgorithmListIndex = new Random().nextInt(hashAlgorithmList.size());//随机选取一个函数int hashCode = hashAlgorithmList.get(hashAlgorithmListIndex).hashCode(key);int index = getIndex(hashCode);String oldKey = array[index];//原本表中这个索引对应的值array[index] = key;//把要插入的值 放到当前索引上key = oldKey; //现在就是要插入原来替换掉的值}if (++reHash >1 || size>=array.length) {//说明要进行扩容操作了expandArray();reHash =0;}else {computeHash();//重新计算hash值}}}/*** 更新 hash函数 重新计算*/private void computeHash() {hashAlgorithmList.clear();//清空原有的函数int one = new Random().nextInt(100);int two = new Random().nextInt(100);two = one == two ? two*2 : two;//只是两个不一样的值hashAlgorithmList.add(new HashAlgorithm(one));hashAlgorithmList.add(new HashAlgorithm(two));rehash(array.length);}private void expandArray() {rehash(nextPrime(array.length*2));}/*** 重新计算所有的 hash 同时放到表中* @param length*/private void rehash(int length) {String [] oldArray = array;array = new String[length];size = 0 ;for (String string : oldArray) {if (string != null) {insert(string);}}}public static void main(String[] args) {Cuckoo cuckoo = new Cuckoo();for (int i = 0; i < 8; i++) {cuckoo.insert("a"+new Random().nextInt(1000));}for (String string : cuckoo.array) {System.out.println(string);}}//素数计算public static Integer nextPrime(Integer begin) {int i;int j;for (i = begin;; i++) {boolean flag = true;for (j = 2; j <= i / 2; j++) {if (i % j == 0) {flag = false;break;} else if (i % j != 0) {continue;} else {break;}}if (flag) {return i;}}}/*** 是否包含当前元素* @param key* @return*/Boolean cotains(String key){for (HashAlgorithm hashAlgorithm : hashAlgorithmList) {int hashCode = hashAlgorithm.hashCode(key);int index = getIndex(hashCode);if (array[index] !=null ) {return true;}}return false;}/*** 获取hash值对应的表中索引* @param hashCode* @return*/int getIndex(int hashCode){int index = hashCode % array.length;index =  index < 0 ? index + array.length : index;return index;}public Cuckoo() {this(DEFAULTSIZE);}public Cuckoo(int size) {array = new String[size];}public int getSize() {return size;}//定义散列函数集合class HashAlgorithm{private int initNumber;public HashAlgorithm(int initNumber) {super();this.initNumber = initNumber;}public int hashCode(String key){return (initNumber +key).hashCode();//传递进来的固定值 +key 模拟两个不同的 hashcode}}
}