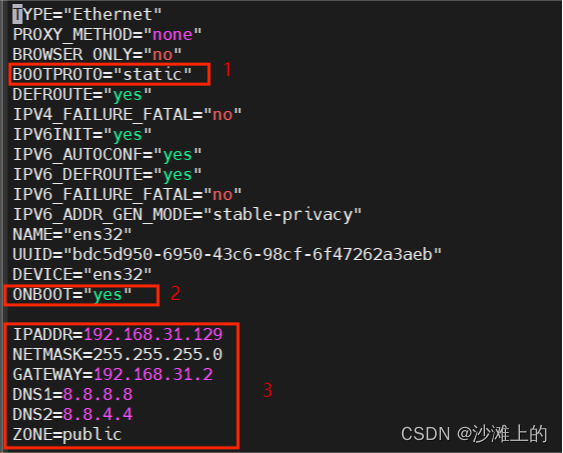
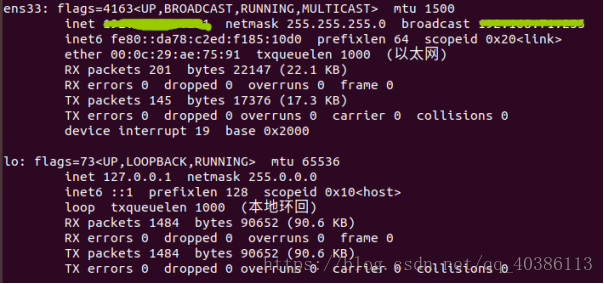
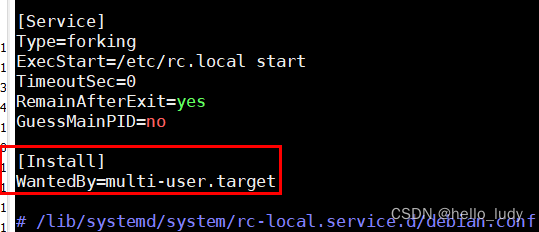
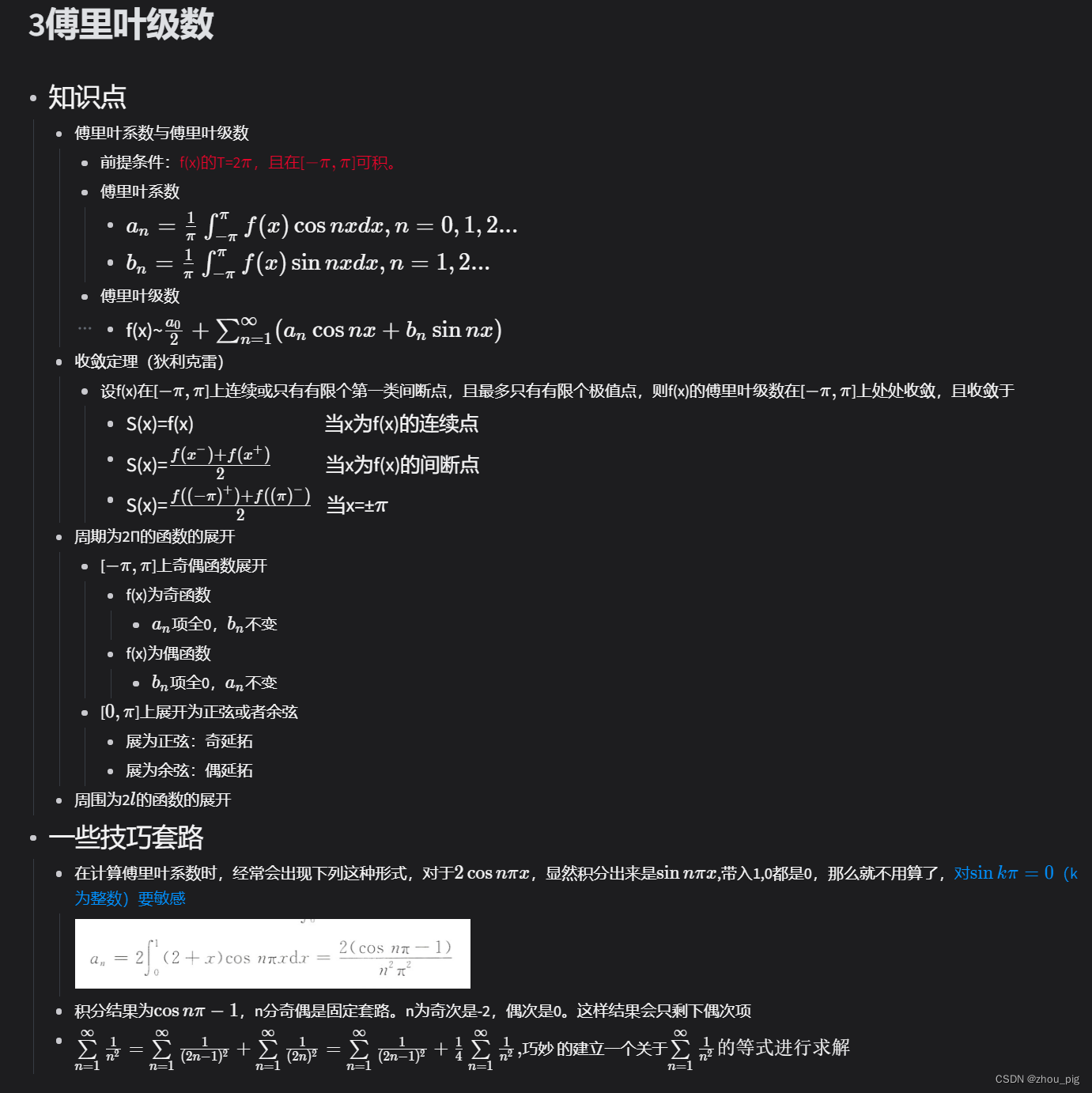
网络环境(免密码认证)
1 客户端生成密钥对ssh-keygen -t rsa
2 公钥发给服务器公钥字符串存放到/home/dev/.ssh/authorized_keys(在/etc/ssh/sshd_config中的authorized_keys 配置项指定)
3 重启ssh服务
项目环境
两个重点知识点
xshell下拷贝文件(这两个命令只限于xshell)
rz win----》linux (需要安装)
sz linux—》win
kill lsof -ti :8000 杀死进程
1 python虚拟环境export WORKON_HOME=/data/virtualsource /usr/local/bin/virtualenvwrapper.shmkvirtualenv -p python3 django
2 xshell下拷贝文件rz win----》linuxsz linux---》win3 django 源码安装查看INSTALL文件pyton setup.py build(可选)python setup.py install
4 创建django项目1 创建项目django-admin startproject itcast2 创建apppython manage.py startapp3 创建页面修改views.py----->返回一个httpresponse4 注册应用修改settings.py文件5 url路由修改urls.py文件5 pcre动态库安装1 查看INSTALL2 ./configure(检查系统依赖,指定安装路径,裁剪定制软件包)make (编译)make install(安装)
6 nginx 安装1 ./configure --prefix=/data/server/nginx --without-http_gzip_module(指定安装路径在/data/server/nginx,裁掉gzip模块)2 make && make install3 若nginx启动报错:找不到动态库ldd 查找链接路径ln -s 创建软连接ln -s /usr/local/lib/libpcre.so.1 /lib/x86_64-linux-gnu/libpcre.so.17 启动项目1 启动django python manage.py runserver > /dev/null 2>&1 &2 启动nginx/data/server/nginx/sbin/nginx
手动代码发布
2.打包代码(代码服务器执行)cd /home/dev/data/codestar zcf tar_code.tar.gz test1/3. 传输代码cd /data/codesscp dev@192.168.14.51:/home/dev/data/codes/tar_code.tar.gz .4. 关闭应用cd /data/server/nginx/sbin./nginx -s stopkill `lsof -ti :8000`5. 解压代码:cd /data/codestar xf tar_code.tar.gz6. 放置代码cd /data/server/itcast/test1mv views.py /data/backup/views.py-`date +%Y%m%d%H%M%S`cp /data/codes/test1/views.py .7. 开启应用export WORKON_HOME=/data/virtual/source /usr/local/bin/virtualenvwrapper.shworkon djangocd /data/server/itcast/python manage.py runserver > /dev/null 2>&1 &cd /data/server/nginx/sbin./nginx8.检查netstat -ltn | grep 80
简单脚本编写
1 命令罗列2 固定内容变量化(方便修改)3 功能函数化(方便扩展)
远程执行命令
ssh dev@192.168.14.51 "bash /home/dev/data/scripts/tar_code.sh"(登陆到代码服务器,执行打包代码的脚本)
大型脚本编写
1 确定框架将功能定义成函数2 命令填充将之前记录的命令填到函数里3 日志功能1 定义写日志函数获取时间日期步骤等信息,拼接后重定向到文件2 各个步骤调用该函数4 锁文件功能(保证脚本同一时间只执行一次)1 创建加锁和解锁函数创建和删除锁文件(/tmp/XXXXX)2 在所有步骤之前调用加锁函数,所有步骤之后调用解锁函数3 部署函数调用之前先判断锁文件是否存在5 功能参数化(方便后续扩展)通过case语句,判断参数,若是deploy则执行deploy函数安全性参数个数的判断($#)
脚本调试
-n 检查语法错误
-v 先显示脚本内容,然后指向
-x 显示一条执行一条