自动控制理论根轨迹的学习过程中，经常会遇到几个问题：

1. 为什么要用根轨迹法？
2. 为什么根轨迹法最终转化为调整增益K来反应系统的稳定性和动态性能？
3. 为什么根轨迹法用开环传递函数求解的却是闭环极点？

盲目的借助于matlab进行根轨迹的计算和绘图，有时候往往不得其深意，可以从基础的定义去梳理我们为什要用根轨迹法，以及根轨迹能解决什么问题。只有明白了根轨迹的目的，我们才能将根轨迹法作为一种工具，真正做到为我们所用。闲话少叙，开始正题。

根轨迹的定义

自动控制系统的稳定性取决于特征根的值（闭环极点），系统的品质取决于闭环系统的极点和零点，如果系统具有可变的增益，那么闭环极点的位置将取决于环路增益K的选取，即可通过简单的增益调整将闭环极点移动到所需位置，那么设计的目的将转化为选择合适增益值的问题。当环路增益K变化时，闭环极点在S平面内的移动，即为根轨迹。
控制系统的闭环极点就是特征方程的根，求解高次特征方程的根是较为繁琐的，当增益K变化时，特征根也在变化，因此，直接求解闭环特征方程根进行控制系统的计算过于繁琐。1948年Evans根据反馈系统开环和闭环传递函数间的关系，提出一种由开环传递函数直接寻求闭环极点，而无需求解高阶系统特征根的方法，即根轨迹法。
所谓根轨迹，指系统的某个特定的参数，在特定范围内变化时，闭环极点在S平面内的运动轨迹。分为常规根轨迹和广义根轨迹法，常规根轨迹的参数变量为增益K，广义根轨迹参数变量为时间常数，反馈系数和开环零极点等。

幅值条件和相角条件

假设控制系统，G为开环传递函数，H为负反馈传递函数，表示为：

则闭环传递函数为：

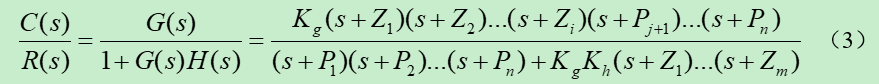
这里就可以解决我们对问题3的疑惑，即闭环传递函数的零点分别为G(s)的零点H(s)的极点。接下来看闭环传递函数极点的求解。

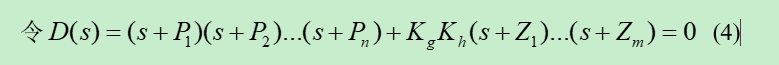
由式4可以看出D(s)为一个高阶代数方程，对其求根很不方便，甚至没有解析解，而且很难看出闭环极点和参数间的关系。接下来我们采用根轨迹法，把其等价为根轨迹方程：

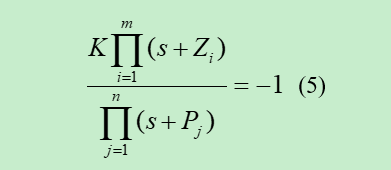
这下对于问题3闭环极点的求解，已经完全转化为了对于D(s)和根轨迹方程根轨迹的求解问题啦。让我们从新审视下根轨迹的定义，即系统的某个特定的参数，在特定范围内变化时，闭环极点在S平面内的运动轨迹。这下关于根轨迹的几个疑问就解决了。
接下来求解闭环极点问题，则闭环传递函数的闭环极点须同时满足幅值和相角条件，由式6和7可知，幅值条件为一个与K相关的函数，相角条件与K值无关，即满足相角条件的s，总能找到一个与之对应的满足幅值条件的K值，即根轨迹由相角条件确定。

根轨迹的绘制

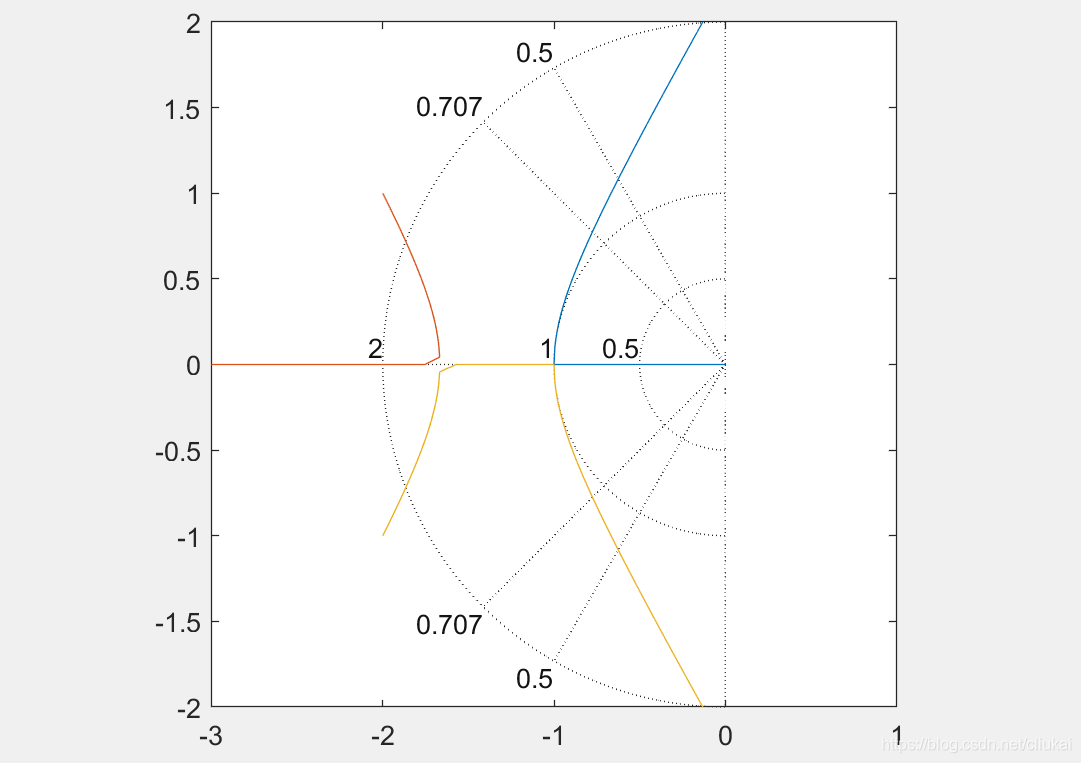
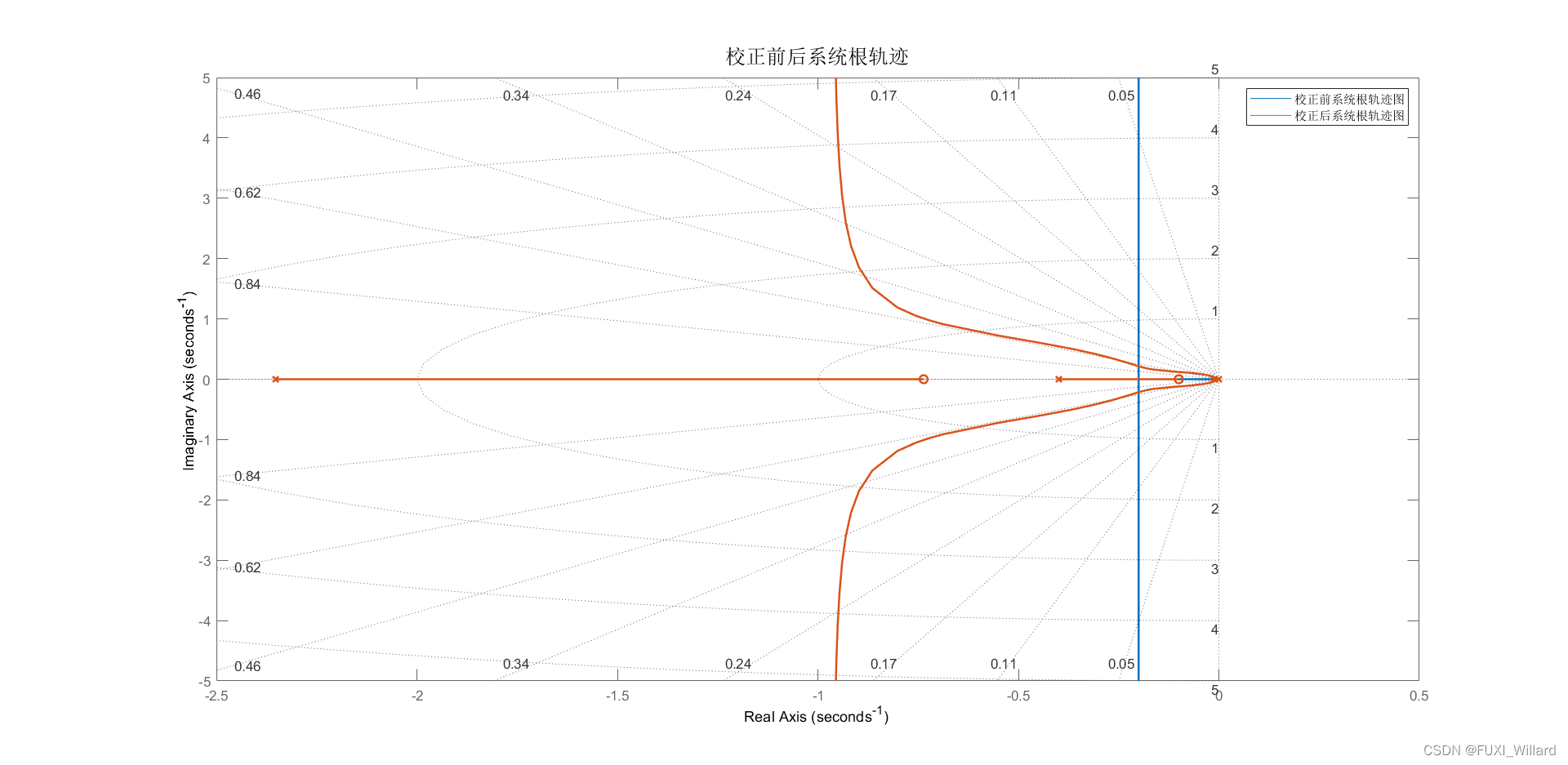
接下来继续讨论根轨迹的绘制法则，参照根轨迹绘制的8大法则，可以绘制出满足需求的根轨迹曲线，借助于matlab工具对根轨迹的分析，工程人员已经无需将精力放在根轨迹的绘制工作上，从而把重点放在对于根轨迹的分析和理解上。
法则1：根轨迹的分支数，连续性和对称性。
对与确定的系统，根轨迹分支数等于开环极点数，根轨迹是一簇连续的曲线，又因为特征方程的根是实根或者是共轭复根，所以根轨迹关于实轴对称。
法则2：根轨迹的起点和终点。
根轨迹的起点为开环极点，终止于开环零点或无穷远处。
法则3：实轴上的根轨迹。
实轴开环零极点数之和为奇数，则实轴段为根轨迹的一部分。
法则4：根轨迹的渐近线。
法则5：根轨迹的分离点和汇合点。
法则6：根轨迹的起始角和终止角。
法则7：根轨迹与虚轴的交点。
法则8：根轨迹任一点对应的增益K。
借助于matlab绘制的根轨迹曲线，无须进行复杂的计算，即可求得法则4-8相关的参数，从而将重点放在对于根轨迹图的理解上。

参考文献

《自动控制理论》第三版. 邹伯敏主编。