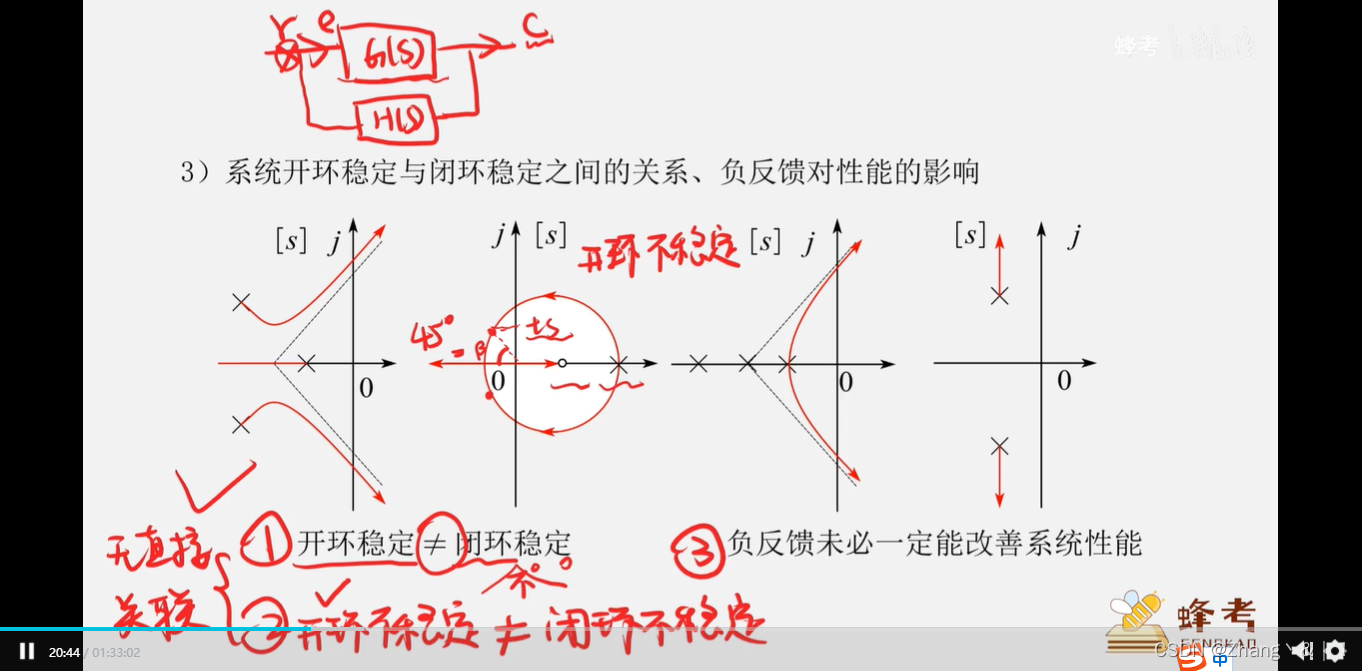
根轨迹法：随着低频环路增益的变化，追踪闭环传递函数的极点和零点在复平面上的变化趋势。

                                                            

其中相角条件是决定根轨迹的充要条件，s平面上一点若满足相角条件，则一定在根轨迹上，幅值条件为必要条件。

再通过幅值方程求出K值，K即为1+betaH中betaH的低频增益。

假设一个三重极点的放大器开环函数为：

                                                                 

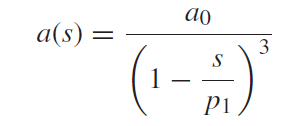
                     接成闭环后：

                                                                 

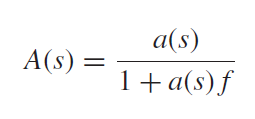
                     将1式代入得到：

                                                         

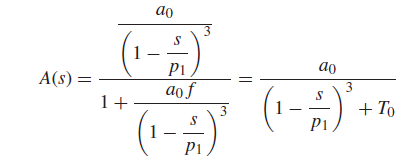
如果闭环系统的极点都位于左半平面，系统是稳定的，否则系统是不稳定的，可以在根轨迹穿过jw轴时候求出临界的增益

假设开环P1=1e9 rad/s，接成单位增益反馈，则闭环分母中f=1，a0f=a0，在matlab中画出根轨迹。G为开环传递函数，等效可以看做是plot的闭环极点与开环低频增益a0的关系。

G=tf(1,[conv(conv([1e-9,1],[1e-9,1]),[1e-9,1])])
rlocus(G);
axis([-2e9 1e9 -2e9 2e9])

                                       

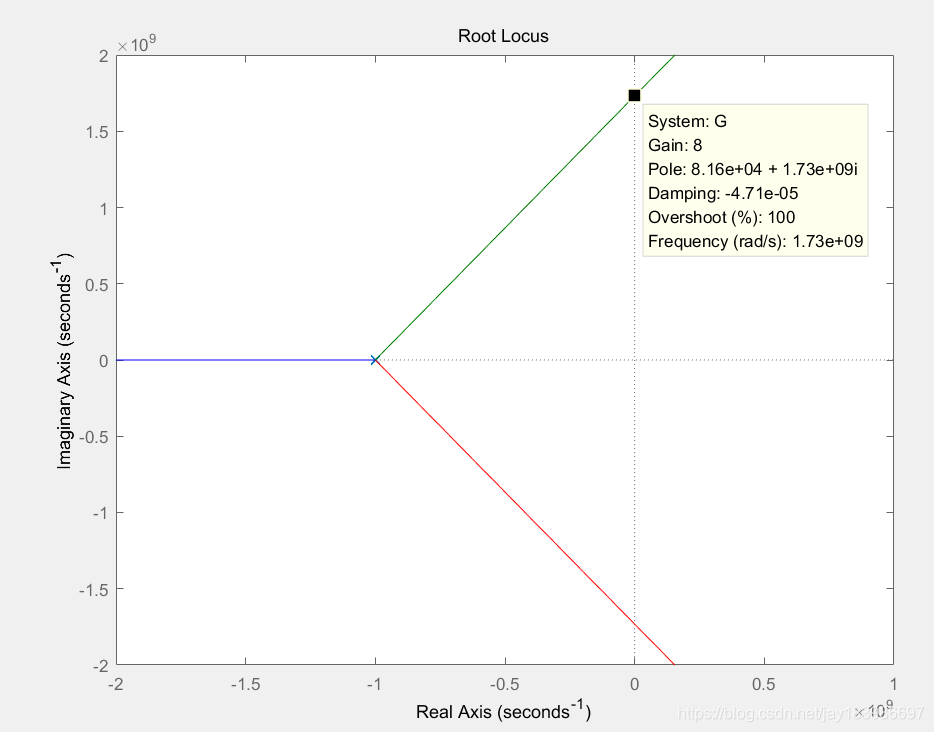
可以看到当环路增益a0f即a0等于8时候，极点开始离开左平面，也说明要想起振，三级环形振荡器中每级的低频增益要大于2，随着震荡开始，信号通路上各级电路发生非线性，最终使得平均的环路增益还是等于1。

 

同样，与nyquist稳定性判据对应，我们可以画出A0=8时候的nyquist图：

G=tf(8,[conv(conv([1e-9,1],[1e-9,1]),[1e-9,1])])
nyquist(G)

                                         

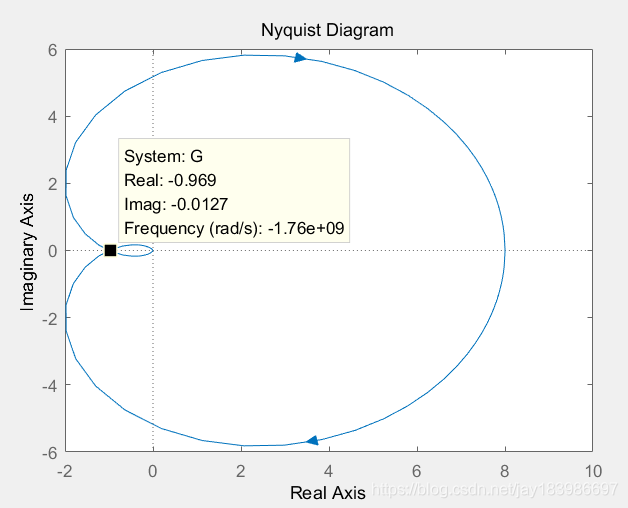
可以看到当a0=8时候，奈奎斯特图正好穿过-1,0点，并且顺时针两次，因此有两个极点在虚轴上面。

同时也可以plot出时域阶跃响应与a0值的对应关系：

Y=[];
for K=[1:1:6]
    GK=feedback(K*G,1);
    step(GK);
    hold on;
end
hold off;