1 根轨迹法基础知识

什么是根轨迹

随着开环增益K的改变，闭环极点也将发生改变，从而在平面上产生一系列的点，这些点的轨迹，就叫做根轨迹。

根轨迹有什么用

闭环系统瞬态响应的基本特性和闭环极点位置密切相关。

在设计中，常常利用增益调整，将闭环极点移动到需要的位置上。

什么是根轨迹法

根轨迹法是一种图解法，由W.R.伊凡斯（Evans）提出，图像反应了特征方程的根和系统中某一个参数数值关系的方法。通常这个参数取开环增益，并命令这个参数在0到无穷大之间进行变化。

2 根轨迹图

幅值和幅角条件

在这里插入图片描述

构造系统的闭环传递函数，得到闭环系统的特征方程（即分母为0），然后分解成幅度值和幅度角两个方程。

$\{KG(s) H(s)\}=\pm 180^{\circ}(2 k+1)$

$|\mathrm{KG}(\mathrm{s}) \mathrm{H}(\mathrm{s})|=1$

满足这两个方程的s值，就是特征方程的根，就是闭环极点。

只满足幅角条件的点构成的图形就是根轨迹（同时满足满足幅值条件就变成了特定的点）。

手绘根轨迹图

根轨迹的几个性质：

K=0对应的特征方程根，就是根轨迹的起点。
根轨迹的数量，就是特征方程的阶数，也就是s的最高次数。

具体步骤

确定实轴上的根轨迹。（尝试把试验点放在实轴上）
确定根轨迹的渐近线。（尝试将s设定为无穷大）
确定分离点。分离点就是s平面上特征方程有重根的点，随着K的增大，根轨迹点将脱离实轴，向复平面运动。
确定根轨迹和虚轴的交点。（利用劳斯稳定判据）

如果极点是一对共轭复数根，则需要确定出射角和汇合点，出射角决定了根轨迹是向实轴运动，还是向复平面运动。

经验和特性

根轨迹分支起始于开环极点，终止于开环零点，分支数等于特征方程根的数目。
根轨迹在s平面中，上下对称，对称轴为实轴。
在根轨迹图上任取一点，可以求出K值。K值是s点到各极点距离乘积，与s到各零点距离的乘积的比值。
如果开环极点数目，比有限开环零点数目多3个或以上，必定存在一个K，当增益超过K时，根轨迹进入右半平面。

3 用MATLAB绘制根轨迹

基本命令是rlocus

rlocus(num,den)
rlocus(A,B,C,D)

使用符号画图可以先把计算结果保存起来，然后使用plot

r = rlocus(num, den)
plot(r, 'o')
plot(r, 'x')

设定绘图区域和长宽比

v = [-6 6 -6 6];
axis(v);
axis('square')

画一个简单的根轨迹图

a = [1 1 0];
b = [1 4 16];
c = conv(a,b);
den = c;
num = [1 3];
rlocus(num,den)
v = [-6 6 -6 6];	# 确定可视区间
axis(v);
axis('square');		# 拉伸成正方形
grid;				# 画出网格

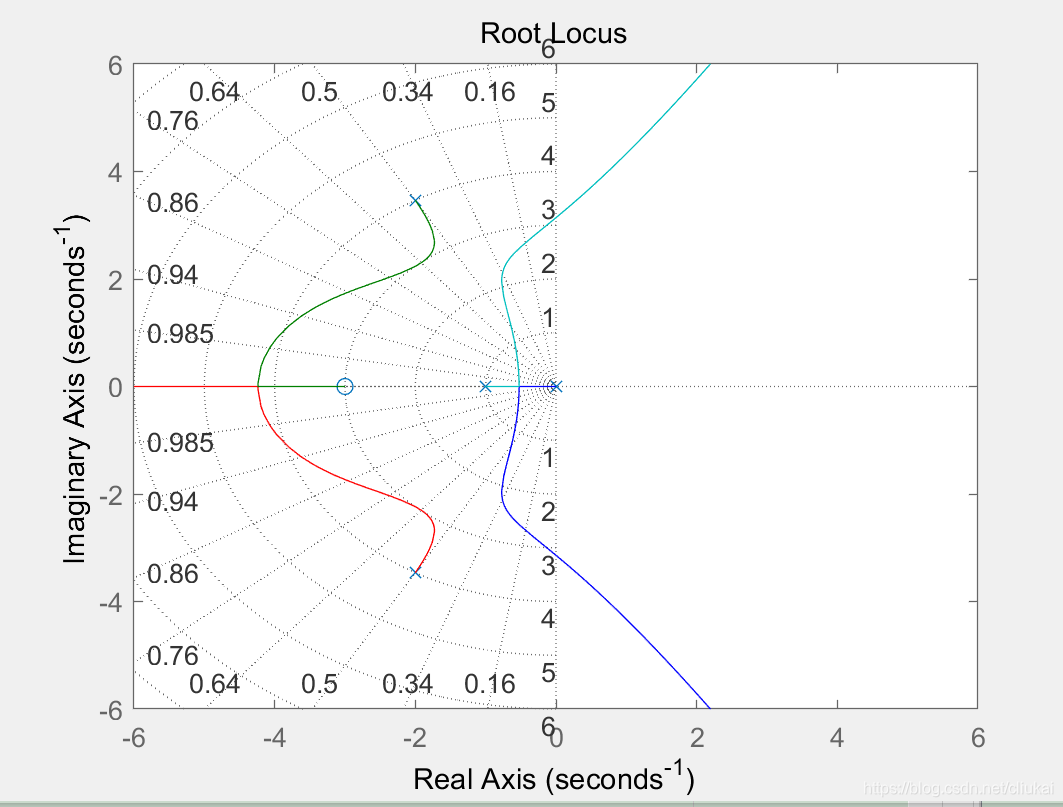
在这里插入图片描述

指定K的取值范围绘制根轨迹

num = [1];
den = [1 1.1 10.3 5 0];
K1 = 0 : 0.2 : 20;			
K2 = 20 : 0.1 : 30;
K3 = 30: 5 : 1000;
K = [K1 K2 K3]					# 对不同的区间，取不同的密度
r = rlocus(num, den, K);
plot(r, 'o')

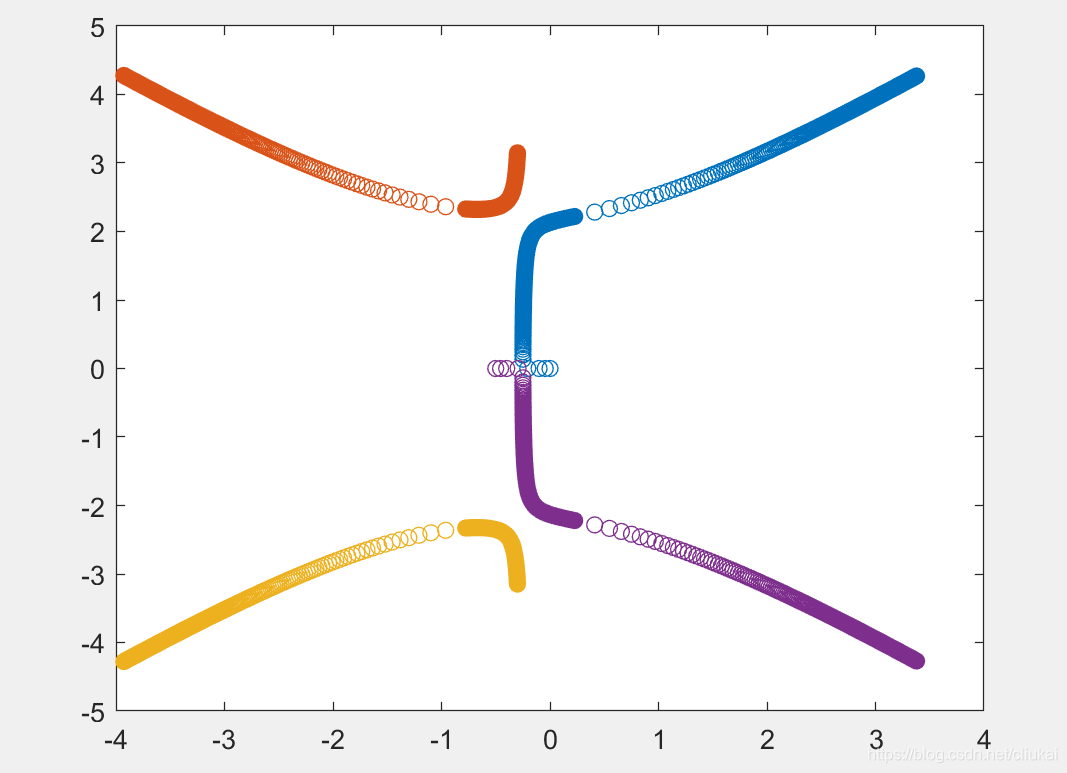
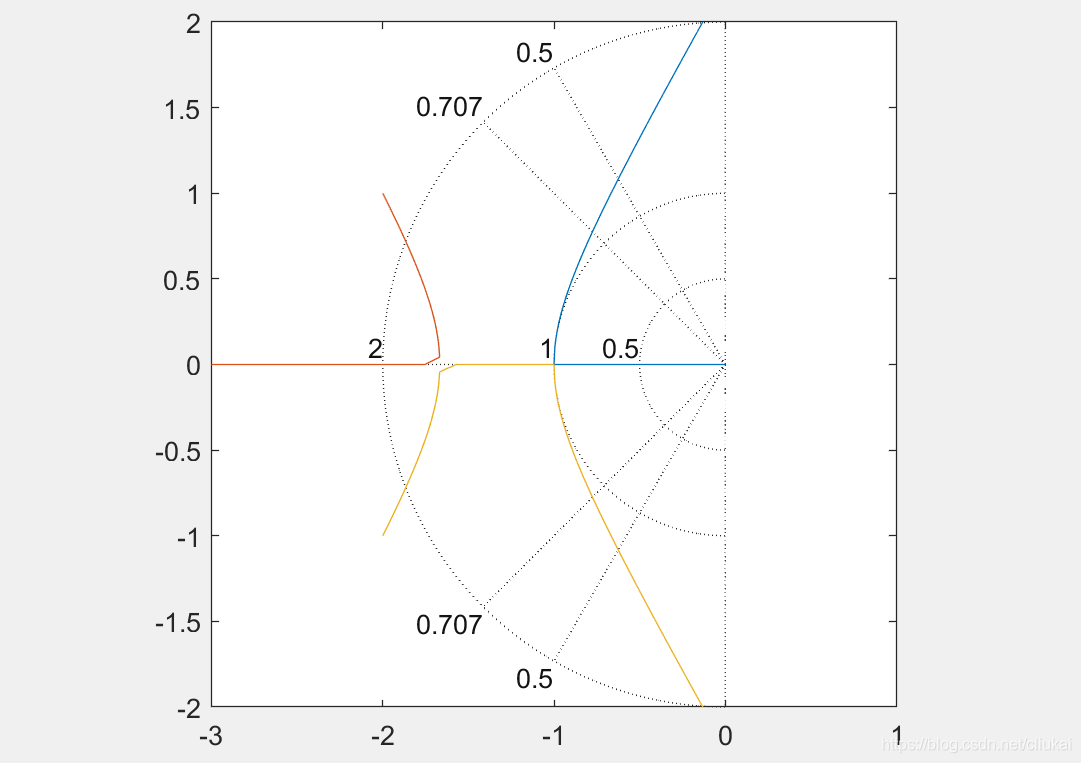
在这里插入图片描述

绘制极网格

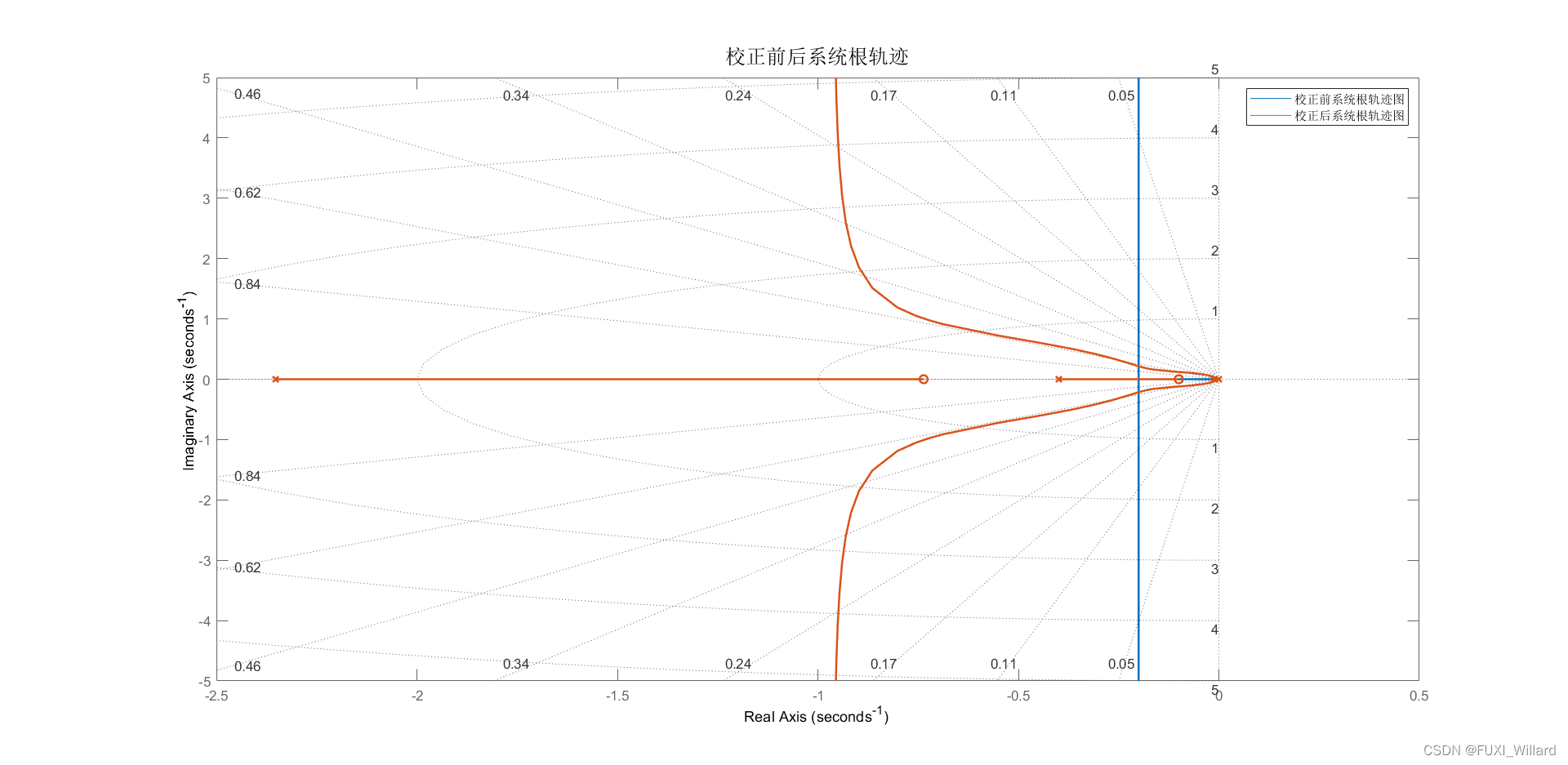
sgrid命令可以把定常阻尼比和定常自然频率圆覆盖到根轨迹图上。

num = [1];
den = [1 4 5 0];
K = 0:0.01:1000;
r = rlocus(num,den,K);
plot(r,'-');
v = [-3 1 -2 2];
axis(v);
axis('square');
sgrid([0.5,0.707],[0.5,1,2]);		# 分别是射线和半圆

在这里插入图片描述