一、稳定性能

根轨迹法的核心思路是：通过研究系统特征方程的根随着传递函数中某一参数从0到∞变化时而变化形成的轨线。

闭环系统稳定性的充分必要条件：系统所有特征根均具有负实部。 表现在根轨迹中，就是所有的根取值均不进入右半平面。

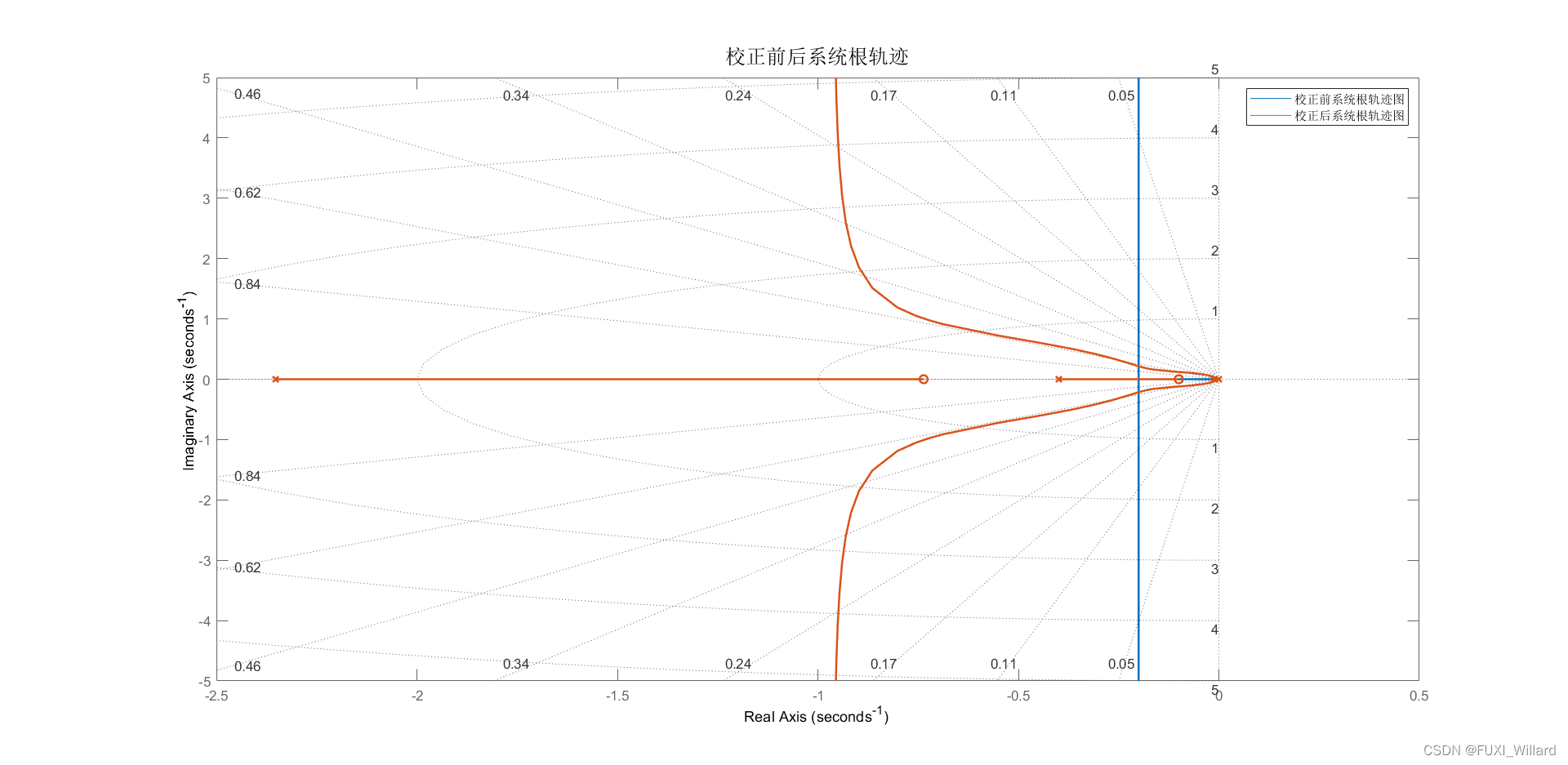
以上一篇博文【自动控制原理】根轨迹法之绘制根轨迹 中的例子：$$W(s)=\frac{K_g^{\ast }(s+3)}{(s+1)(s+2)(s^2+s+1.25)}$$为例，我们已经画出其根轨迹为：

可以看出，随着$K_g^{\ast }$从$0$变化到无穷时，有一对共轭复根从$(-0.5\pm j)$变化到无穷。可以看出，必然存在某一个$K_{g_o}^{\ast }$使得在此时，该共轭复根恰好运行到虚轴，此时系统位于临界处。

反之，如果根轨迹始终位于虚轴左侧，则系统不论参数如何变化，始终是稳定的。因此，通过根轨迹可以看出系统的稳定性能。

如果要求临界稳定的$K_g^{\ast }$值，则可以利用绘制法则7求解，如上例子中：
闭环特征方程$D(s)=s^4+4s^3+6.25s^2+5.75s+2.5+K_g^{\ast }s+3K_g^{\ast }=0$，令$s=j\omega$
得$D(j\omega )={\omega }^4-4{\omega }^{3}j-6.25{\omega }^2+5.75\omega j+2.5+K_g^{\ast }\omega j+3K_g^{\ast }=({\omega }^4-6.25{\omega }^2+2.5+3K_g^{\ast })+(K_g^{\ast }\omega +5.75\omega -4{\omega }^3)j=0$
所以$$\{\begin{array}{c}{\omega }^4-6.25{\omega }^2+2.5+3K_g^{\ast }=0\\ K_g^{\ast }\omega +5.75\omega -4{\omega }^3=0\end{array}$$解得$K_g^{\ast }=1.9398或-36.44（舍），\omega =1.3865$
因此解得$K_g^{\ast }\in (0,1.93)$时，系统是稳定的，临界稳定时，这对共轭复根运行至$\pm 1.3865j$处。
注：解得的$K_g^{\ast }$不可以取1.94，虽然这样取值满足四舍五入，但是系统稳定时，$K_g^{\ast }$并不会超过$1.9398$，所以应当向下取整。

二、系统参数设计

设计系统参数，即根据变化的根轨迹，求解满足要求的$K_g^{\ast }$：
$Step1$：首先按照刚才所述求解出系统稳定的$K_g^{\ast }$范围，在该前提下，求解系统参数。
$Step2$：通常根据阻尼角大小，绘制一条辅助线，求解与根轨迹的交点
$Step3$：该点即是系统期望配置的特征根所在位置，求出该位置处的$K_g^{\ast }$即可。

三、偶极子对、主导极点、开环零点

3.1 偶极子对

偶极子对是指：一对零极点相距很近，又非常靠近原点，且极点位于零点右侧，称之为偶极子对

利用偶极子对，可以改善系统的稳态性能。如果不考虑稳态性能时，则可以在传递函数中将互为偶极子的因式对消，从而实现降阶。

3.2 主导极点

主导极点指：距离虚轴最近的极点，其实部小于其他极点的1/5，且周围不存在零点，称之为主导极点。

利用主导极点，可以认为系统性能较大程度取决于主导极点，从而实现降阶。

3.3 开环零点

增加开环零点，会使得根轨迹左偏，有利于提高系统的稳定性。如本文刚开始那个例子中，若要使得根轨迹不偏向于右半平面，可以考虑为系统增加零点。