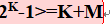海明校验码
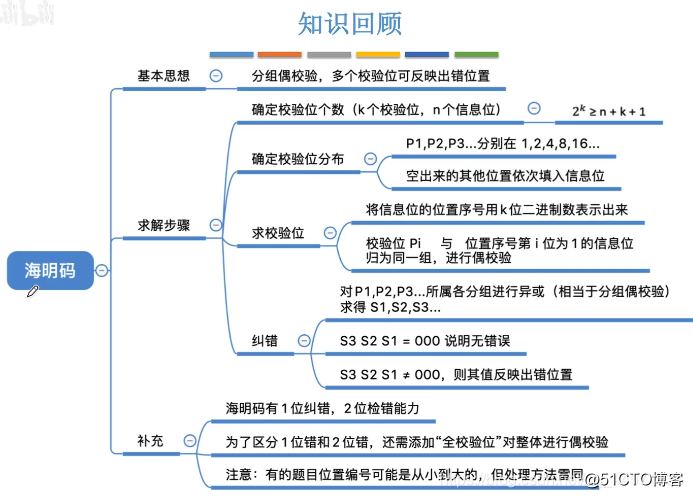
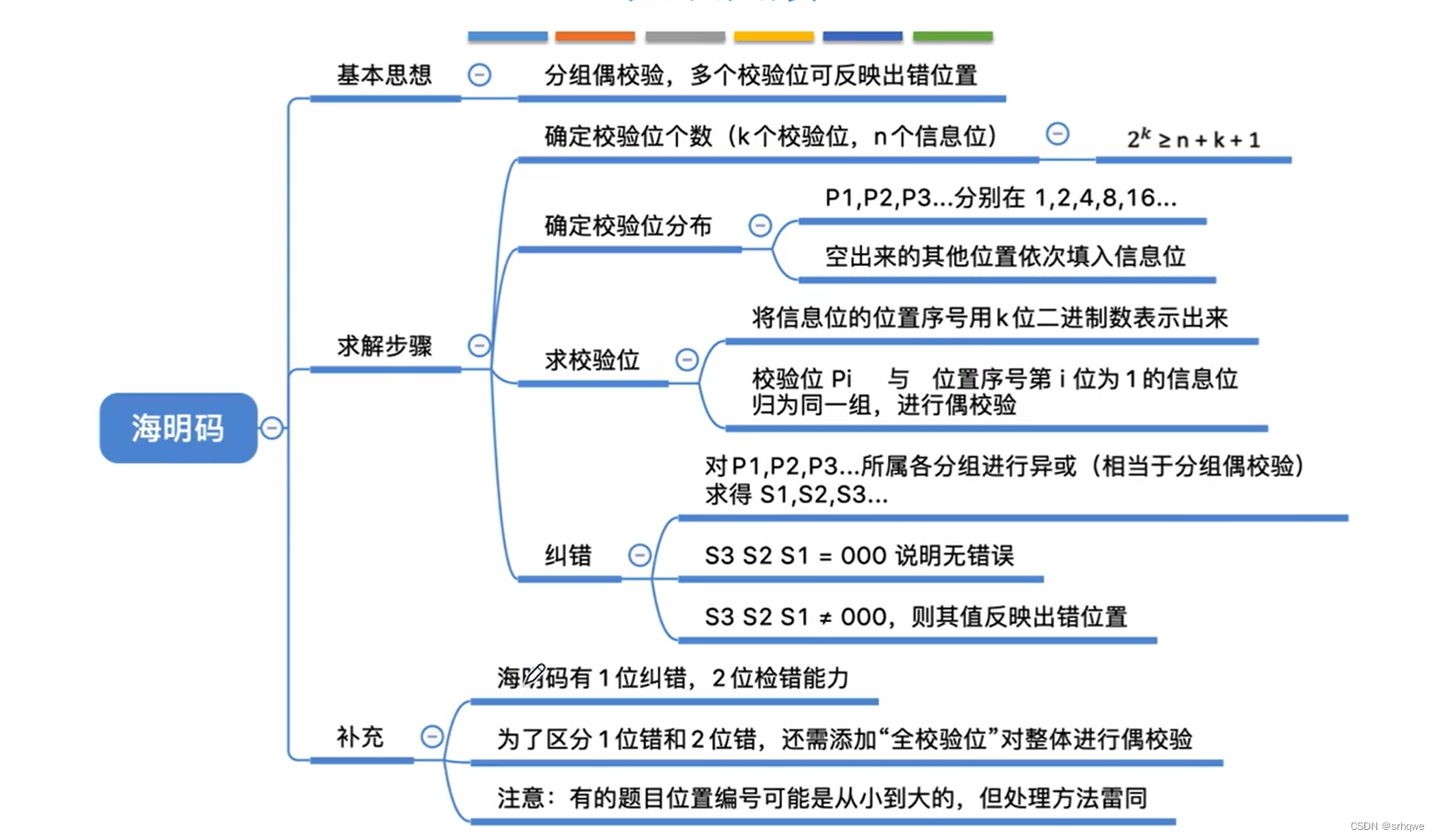
海明校验码思路
偶校验:1010 → 01010,能发现奇数位错误,但无法确定是哪一位出错 → 1个校验位只能携带2种状态信息:对/错
海明码设计思路:将信息位分组进行偶校验 → 多个校验位能携带多种状态信息(对/错,错在哪)
需要多少校验位:
校验码 = 信息位(n) + 校验位(k) + 1(对错状态)
2^k种状态 >= n + k + 1
若n = 4, 则k = 3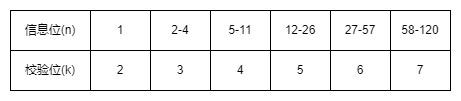
海明码求解步骤
例:信息位:1010
确定海明码的位数
∵ 2^k >= n + k + 1
∴ n = 4, k = 3
设信息位1010 => D4 D3 D2 D1 共4位,设校验位P3 P2 P1 共3位
对应海明码:H7 H6 H5 H4 H3 H2 H1确定校验位的分布
校验位Pi放在海明位号为2^i-1(H1 H2 H4, 也可以理解为权值)的位置
信息位按顺序放到其余位置(H3 H5 H6 H7)
海明码分布顺序为:D4 D3 D2 P3 D1 P2 P1
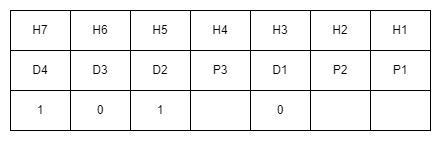
求校验位的值
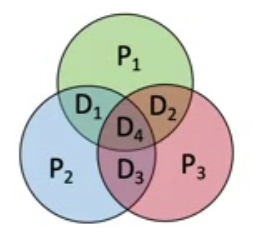
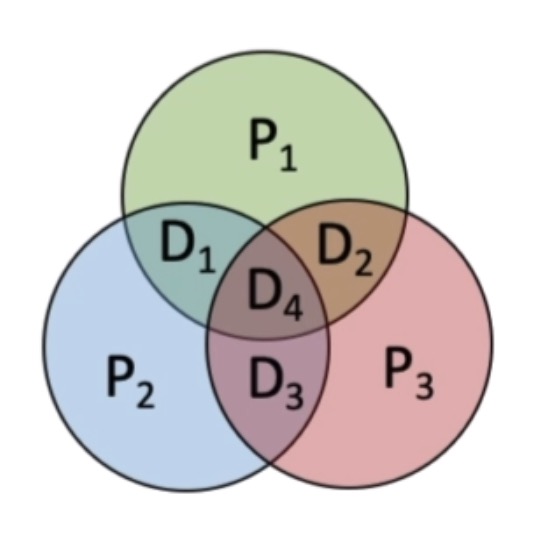
海明码分组:将信息位对应的海明位号值转换为二进制,各取二进制中的一位进行编组
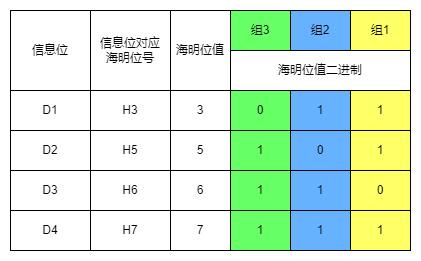
校验位值Pi = 组i中值为1的海明位下的信息位进行异或运算
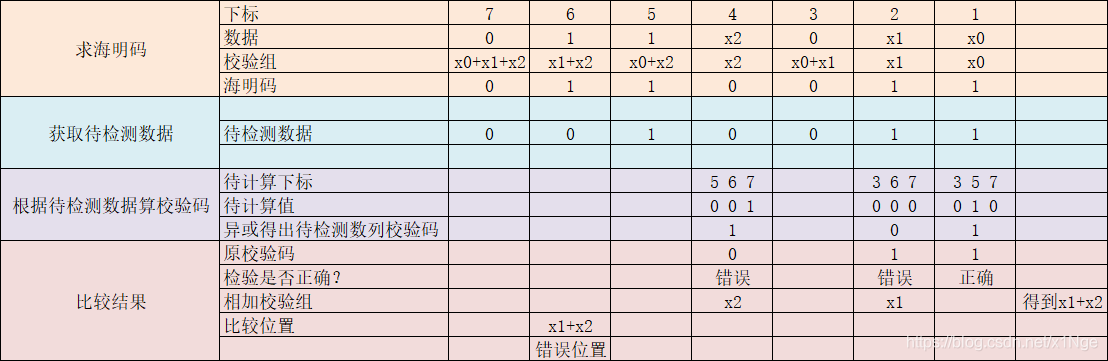
P1 = H3⊕H5⊕H7 = D1⊕D2⊕D4 = 0⊕1⊕1 = 0
P2 = H3⊕H6⊕H7 = D1⊕D3⊕D4 = 0⊕0⊕1 = 1
P3 = H5⊕H6⊕H7 = D2⊕D3⊕D4 = 1⊕0⊕1 = 0
纠错
Si = Pi ⊕ 组i;S1 S2 S3 = 000即为正确,否则结果为错误值的位置
例:接收到海明码 1010010
S3 = P3⊕D2⊕D3⊕D4 = 0⊕1⊕0⊕1 = 0
S2 = P2⊕D1⊕D3⊕D4 = 1⊕0⊕0⊕1 = 0
S1 = P1⊕D1⊕D2⊕D4 = 0⊕0⊕1⊕1 = 0
校验结果为 000,正确例:接收到海明码 101000(H2跳变)0
S3 = P3⊕D2⊕D3⊕D4 = 0⊕1⊕0⊕1 = 0
S2 = P2⊕D1⊕D3⊕D4 = 0(跳变)⊕0⊕0⊕1 = 1
S1 = P1⊕D1⊕D2⊕D4 = 0⊕0⊕1⊕1 = 0
校验结果为 010,错误位=010=2=H2=P2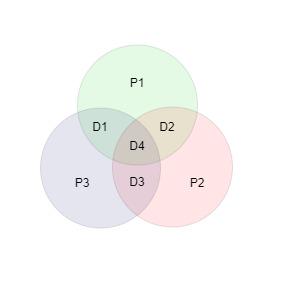
全校验
按上述方式如果发生2位跳变,则无法纠错,因此需要加上全校验位H8,对整体进行偶校验
S3S2S1 = 000 && 全体偶校验成功 => 正确
S3S2S1 != 000 && 全体偶校验失败 => 有1位跳变,纠正即可
S3S2S1 != 000 && 全体偶校验成功 => 有2位跳变(跳变位数为偶数),重新传输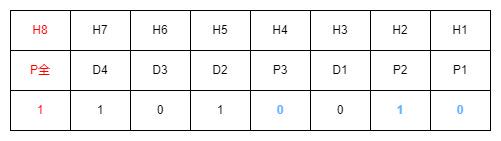
海明校验码有1位纠错能力,2位检错能力