一、EM算法介绍
我们经常会从样本观察数据中,找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。(最大似然估计:利用已知的样本结果,反推最有可能导致这样结果的一组参数)但是在一些情况下,我们得到的观察数据有未观察到的隐含数据,此时我们未知的有隐含数据和模型参数,因而无法直接用极大化对数似然函数得到模型分布的参数。用EM算法可以解决。
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。
EM算法的每次迭代由两步组成:E步,求期望;M步,求极大。所以被称为期望极大算法。
EM算法解决这个的思路是使用启发式的迭代方法,既然我们无法直接求出模型分布参数,那么我们可以先猜想隐含数据(EM算法的E步),接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解我们的模型参数(EM算法的M步)。由于我们之前的隐藏数据是猜测的,所以此时得到的模型参数一般还不是我们想要的结果。不过没关系,我们基于当前得到的模型参数,继续猜测隐含数据(EM算法的E步),然后继续极大化对数似然,求解我们的模型参数(EM算法的M步)。以此类推,不断的迭代下去,直到模型分布参数基本无变化,算法收敛,找到合适的模型参数。
一个最直观了解EM算法思路的是K-Means算法:在K-Means聚类时,每个聚类簇的质心是隐含数据。我们会假设K个初始化质心,即EM算法的E步;然后计算得到每个样本最近的质心,并把样本聚类到最近的这个质心,即EM算法的M步。重复这个E步和M步,直到质心不再变化为止,这样就完成了K-Means聚类。
二、EM算法推导
1、Jensen不等式
2、极大似然估计法估计参数
(1)极大似然估计思想
总结起来,最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
(2)求解极大似然函数
(3)求最大似然函数估计值的一般步骤
3、求解随机变量的期望
4、EM算法推导
我们的似然函数为:
上面似然函数L(Θ)式中,即式(1),是根据联合概率密度下某个变量的边缘密度函数求解的(这里把z当作是随机变量)。对每一个样本 i 的所有可能类别 z 求联合概率密度函数和,也就得到随机变量x的边缘概率密度。由于对式(1)直接求导非常困难,所以将其分子分母都乘以一个相等的函数Qz,转换为式(2)。而在式(2)变为式(3)的过程,采用的是上面提到的Jensen不等式:
分析过程如下:
所以:
所以有:
即相当于f(Ex)
同理有:
即相当于E(f (x))
根据凹函数的Jensen不等式:
即得到(2)式大于等于(3)式:
则(3)式是(2)式的下限。那么我们可以通过不断的最大化(3)式的值,来使(2)式不断提高,最终达到它的最大值。
进而可得:
5、EM算法步骤
6、EM算法的收敛性
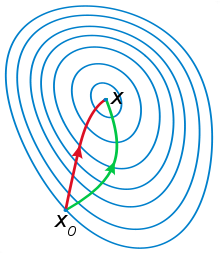
下面这张图很好的说明了EM算法的优化过程:
EM算法可以保证收敛到一个稳定点,但是却不能保证收敛到全局的极大值点,因此它是局部最优的算法,当然,如果我们的优化目标是凸函数,则EM算法可以保证收敛到全局最大值。
7、算法总结
我们的算法里已知的是观察数据,未知的是隐含数据和模型参数,在E步,我们所做的事情是固定模型参数的值,优化隐含数据的分布,而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值。
三、EM算法应用(EM算法用来解决含有隐含数据的极大似然估计/极大后验概率)
1、K-Means聚类(在K-Means聚类时,每个聚类簇的质心是隐含数据):https://www.jianshu.com/p/4f032dccdcef
2、高斯混合模型(高斯混合模型中,每种模型的概率是隐含数据)
什么是高斯混合模型呢?就是说,任何一个数据的分布,都可以看作是若干高斯分布的叠加。

如图所示,如果P(X)代表一种分布的话,存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。有意思的是,这种拆分方法已经证明出,当拆分的数量达到512时,其叠加的分布相对于原始分布而言,误差是非常非常小的了。
(1)高斯分布
高斯分布(Gaussian distribution)有时也被称为正态分布(normal distribution),是一种在自然界大量的存在的、最为常见的分布形式。
由334个人的身高数据构成的正态分布直方图
这个图形非常直观的展示了高斯分布的形态,接下来看下严格的高斯公式定义,高斯分布的概率密度函数公式如下:
(2)高斯混合模型
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。
如图1,图中的点在我们看来明显分成两个聚类。这两个聚类中的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM,那么只能用一个的二维高斯分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理,毕竟肉眼一看就觉得应该把它们分成两类。
图1
图2
(3)GMM的应用
(4)GMM的参数估计
(5)EM算法估参流程
附上EM算法手动推导的草稿: