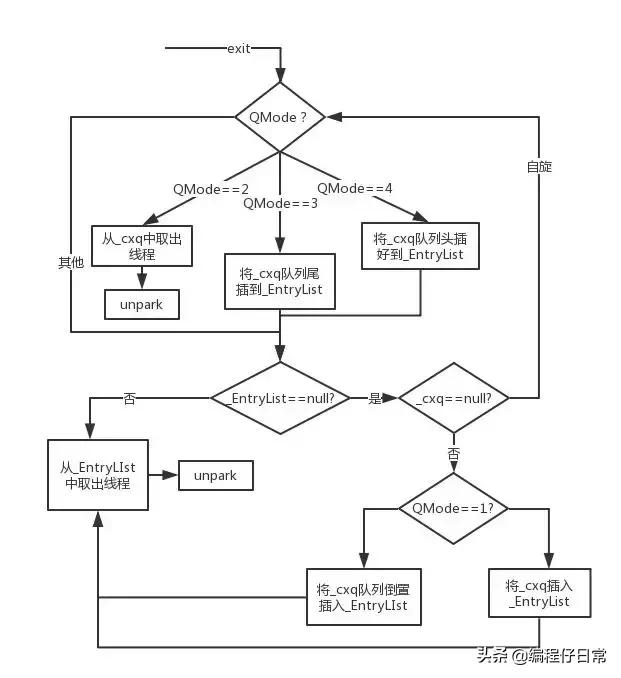
目录
- 牛顿法原理简介
- 使用牛顿法求解一元方程
- 使用牛顿法求解平面定位问题
- 参考文献
牛顿法原理简介
牛顿法的原理是利用函数 f ( x ) f(x) f(x) 的泰勒级数的前几项来寻找方程 f ( x ) = 0 f(x)=0 f(x)=0 的根。
f ( x ) f(x) f(x)在 x 0 x_0 x0处的一阶泰勒展开
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) . f(x) = f(x_0) +f^\prime(x_0)(x-x_0). f(x)=f(x0)+f′(x0)(x−x0).
它的解
x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) . x_1=x_0-\frac{f(x_0)}{f^\prime(x_0)}. x1=x0−f′(x0)f(x0).
进而推出
x n + 1 = x n − f ( x n ) f ′ ( x n ) . x_{n+1}=x_n-\frac{f(x_n)}{f^\prime(x_n)}. xn+1=xn−f′(xn)f(xn).
由此迭代下去求出近似解。
参考百度百科牛顿迭代法.
使用牛顿法求解一元方程
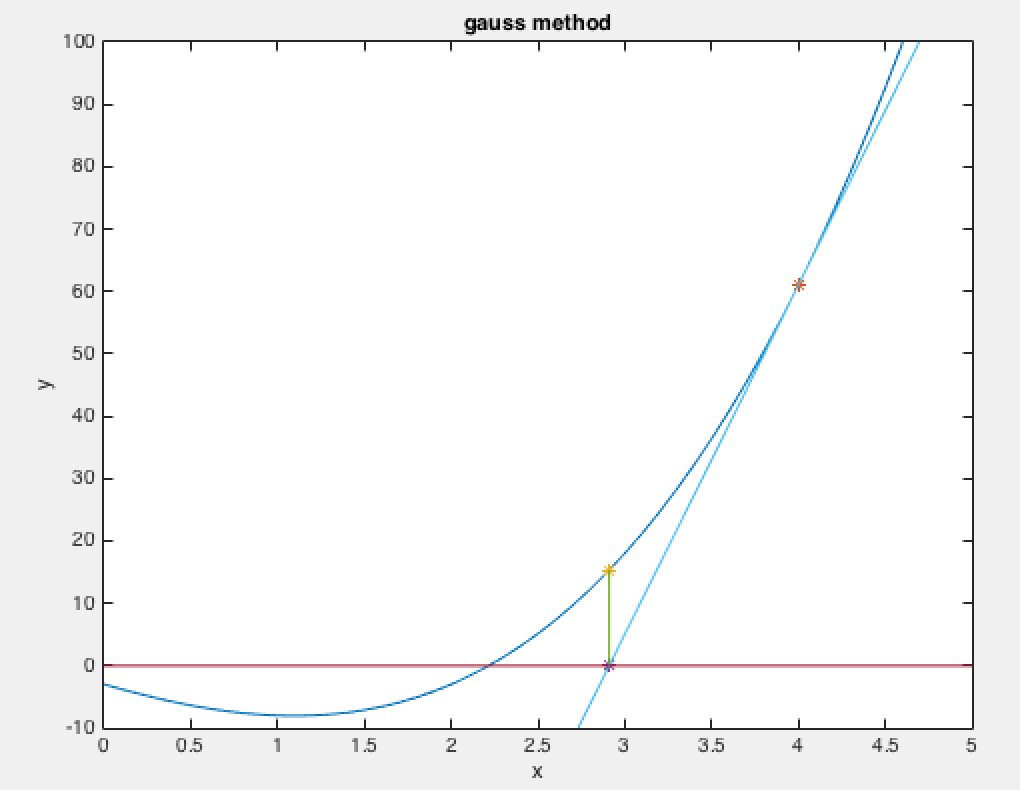
使用牛顿法来解方程
2 = ( x − 1 ) 2 + 2. 2=(x-1)^2+2. 2=(x−1)2+2.
使用牛顿法求解,先给一个初始值 x g u e s s = 10 x_{guess}=10 xguess=10,迭代结果不断逼近真实值。

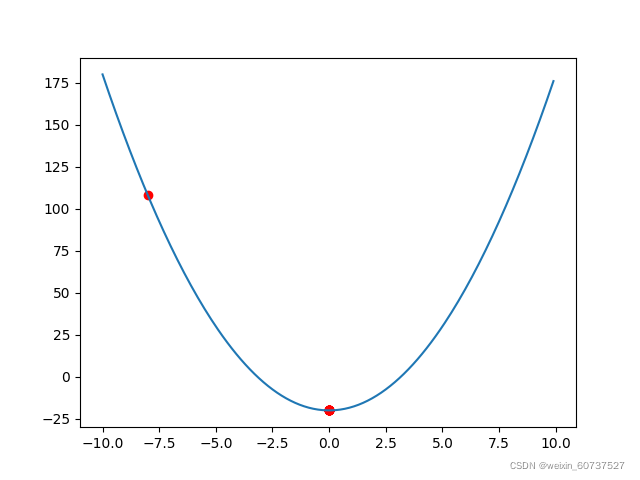
迭代50次的结果与真实值,可以看出,牛顿法迭代逼近真实值的速度非常快,但并不是迭代次数越多越好。

代码如下
%牛顿法求一元二次方程的根 by wuyc
%y=(x-1)^2+2
%y'=2x-2clc; clear all;
xguess = 10;%猜的初始点
N=50;%迭代次数x1=xguess;
x=zeros(N,1);for i=1:N
deltax= -((x1-1)^2+2)/(2*x1-2);%delta x=-f'(xn)/f(xn)
x2 = x1+deltax; %xn+1=xn+delta x
x1=x2;
x(i)=x1;%x是每次迭代的结果
endfigure (1);t=[0:0.1:12];
y=(t-1).^2+2;yx=(x-1).^2+2;plot(t,y,'LineWidth',2);hold on; %画方程曲线plot([xguess,xguess],[0,(xguess-1).^2+2]);
plot([xguess,x(1)],[(xguess-1).^2+2,0]);for ii=1:2
plot([x(ii),x(ii)],[0,yx(ii)]);
plot([x(ii),x(ii+1)],[yx(ii),0]);
end
set(gca,'LineWidth',2);
xlabel('x','FontSize',18);
ylabel('y','FontSize',18);figure (2);plot (x);
hold on
plot ([1,50],[1,1]);%真实值
set(gca,'LineWidth',2);
xlabel('迭代次数');
ylabel('迭代结果');
legend('牛顿法结果','真实值');
使用牛顿法求解平面定位问题
定位问题应用十分广泛,这里我们把问题简化为二维的矩形区域定位。
由四个台站TZ1、TZ2、TZ3、TZ4决定的矩形区域内的某一点mt ( m t r u e ) (m_{true}) (mtrue)发出信号,信号的速度是 v v v,那么根据四个台站接收到的时间的平方dobs( d o b s e r v a t i o n ) d_{observation}) dobservation),我们可以求出信号的位置。(台站只能记录信号出现的时刻,而不能记录到信号传播到台站所需的时间 t t t,这里我们又把问题简化了。)
这里插一句,在反演问题中,我们常把模型参数称为 m m m,数据称为 d d d,所谓反演问题,就是给定数据 d d d求解模型参数 m m m的过程。
因为时间 t t t等于路程 s s s除以速度 v v v,有
t 2 = 1 v 2 × s 2 t^2=\frac{1}{v^2} \times s^2 t2=v21×s2
因此对应的反演问题为
[ d 1 d 2 d 3 d 4 ] = 1 v 2 [ ( x 1 2 − m t 1 2 ) + ( y 1 2 − m t 2 2 ) ( x 2 2 − m t 1 2 ) + ( y 2 2 − m t 2 2 ) ( x 3 2 − m t 1 2 ) + ( y 3 2 − m t 2 2 ) ( x 4 2 − m t 1 2 ) + ( y 4 2 − m t 2 2 ) ] \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ \end{bmatrix} =\frac{1}{v^2} \begin{bmatrix} (x_1^2-mt_1^2)+(y_1^2-mt_2^2) \\ (x_2^2-mt_1^2)+(y_2^2-mt_2^2) \\ (x_3^2-mt_1^2)+(y_3^2-mt_2^2) \\ (x_4^2-mt_1^2)+(y_4^2-mt_2^2) \\ \end{bmatrix} d1d2d3d4 =v21 (x12−mt12)+(y12−mt22)(x22−mt12)+(y22−mt22)(x32−mt12)+(y32−mt22)(x42−mt12)+(y42−mt22)
这里的参数和问题显得有些混乱,主要目的是为了是反演问题简单。简单的说就是操场四个顶点有四个接收器,操场中间某一个点发出一个速度为 v v v信号,发出信号的同时接收器开始计时,因此接收器记录的时刻 t t t就是信号传输的时间。
我们要根据 t t t来求解信号的位置 m m m,为了使反演问题简单,我们把 t 2 t^2 t2看作数据 d d d.
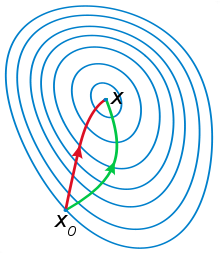
代码运行结果如下,黑点是猜的初始点,绿点是真实点,红点是反演结果。

代码如下
% 根据到时反演信号位置clc;clear all;N=4;
v=100;%速度
%4个台站的位置
TZ1=[0,0];
TZ2=[400,0];
TZ3=[400,600];
TZ4=[0,600];
TZ=[TZ1;TZ2;TZ3;TZ4];
x=TZ(:,1);%台站位置横坐标
y=TZ(:,2);%台站位置纵坐标M=2;%反演的模型参数维度
mt = [100, 100]';%真实的信号位置dtrue = (1/v^2).*[(x-ones(N,1)*mt(1)).^2 + (y-ones(N,1)*mt(2)).^2];%真实的到时的平方
sd=0.4;
dobs = dtrue + random('Normal',0,sd,N,1);%真实值 加上均值是0,方差是sd,N行1列的随机数(随机误差) 生成观测值(到时平方)mg=[400,600]';%mguess 牛顿法需要一个初始点
dg = (1/v^2).*[(x-ones(N,1)*mg(1)).^2 + (y-ones(N,1)*mg(2)).^2];%dg是猜的点到时的平方
Eg = (dobs-dg)'*(dobs-dg);%生成401*601网格
L = 401;
J = 601
Dm = 1;
m1min=0;
m2min=0;
ma1 = m1min+Dm*[0:L-1]';
ma2 = m2min+Dm*[0:J-1]';
m1max = ma1(L);
m2max = ma2(J);% 计算误差
E = zeros(L,J);
for j = [1:L]
for k = [1:J]dpre = (1/v^2).*[(x-ones(N,1)*ma1(j)).^2 + (y-ones(N,1)*ma2(k)).^2];%预测值E(j,k) = (dobs-dpre)'*(dobs-dpre);%误差
end
endfigure(1);
%误差图
set(gca,'LineWidth',2);
hold on;
axis( [m2min, m2max, m1min, m1max] );
imagesc( [m2min, m2max], [m1min, m1max], E);
colorbar;
xlabel('m2','FontSize',18);
ylabel('m1','FontSize',18);
plot( mt(2), mt(1), 'go', 'LineWidth', 3 );%绿色点表示真实值
plot( mg(2), mg(1), 'ko', 'LineWidth', 3 );%黑色是猜的初始点% Newton's method, calculate derivatives
% y = 1/v^2*((x-m1)^2+(y-m2)^2)
% dy/dm1 = 2/v^2*(m1-x)
% dy/dm2 = 2/v^2*(m2-y)%Ehis用来储存每次迭代的误差 m1his、m2his用来储存每次迭代的结果
Niter=10;%迭代次数
Ehis=zeros(Niter+1,1);
m1his=zeros(Niter+1,1);
m2his=zeros(Niter+1,1);
Ehis(1)=Eg;
m1his(1)=mg(1);
m2his(1)=mg(2);G = zeros(N,M);%G矩阵的维度是N*M
for k = [1:Niter]dg = (1/v^2).*[(x-ones(N,1)*mg(1)).^2 + (y-ones(N,1)*mg(2)).^2];%dg是猜的点到时的平方dd = dobs-dg;%猜的值与观测值的差Eg=dd'*dd;Ehis(k+1)=Eg;G = zeros(N,M);%导数矩阵G(:,1) = 2/v^2.*(ones(N,1)*mg(1)-x);G(:,2) = 2/v^2.*(ones(N,1)*mg(2)-y);dm = ((G'*G)^-1)*G'*dd;%最小二乘求解 dm 相当于delta xmg = mg+dm;plot( mg(2), mg(1), 'wo', 'LineWidth', 2 );%画出迭代后的点m1his(k+1)=mg(1);m2his(k+1)=mg(2);plot( [m2his(1+k-1), m2his(1+k) ], [m1his(1+k-1), m1his(1+k) ], 'r', 'LineWidth', 2 );endplot( m2his(Niter+1), m1his(Niter+1), 'ro', 'LineWidth', 2 );%红色是迭代最终结果
此代码参考了William Menke 的Geophysical Data Analysis: Discrete Inverse Theory.
需要指出的是,虽然牛顿法原理简单收敛快,但这个过程并非总能实现,这里就涉及到全局极小和局部极小的问题了。幸运的是上述两个例子不存在这个问题,但在下图中,只有当初始值在红色区域内时,牛顿法才可以收敛到全局极小。

参考文献
链接:
1:牛顿迭代法.
2: Geophysical Data Analysis: Discrete Inverse Theory