有用请点赞，没用请差评。

欢迎分享本文，转载请保留出处。

 

牛顿法也是求解无约束最优化问题的常用方法，有收敛速度快的优点。牛顿法是迭代算法，每一步需要求解目标函数的海赛矩阵的逆矩阵。同时还有拟牛顿法、阻尼牛顿法、修正牛顿法等等。

算法步骤：

 

import random
import numpy as np
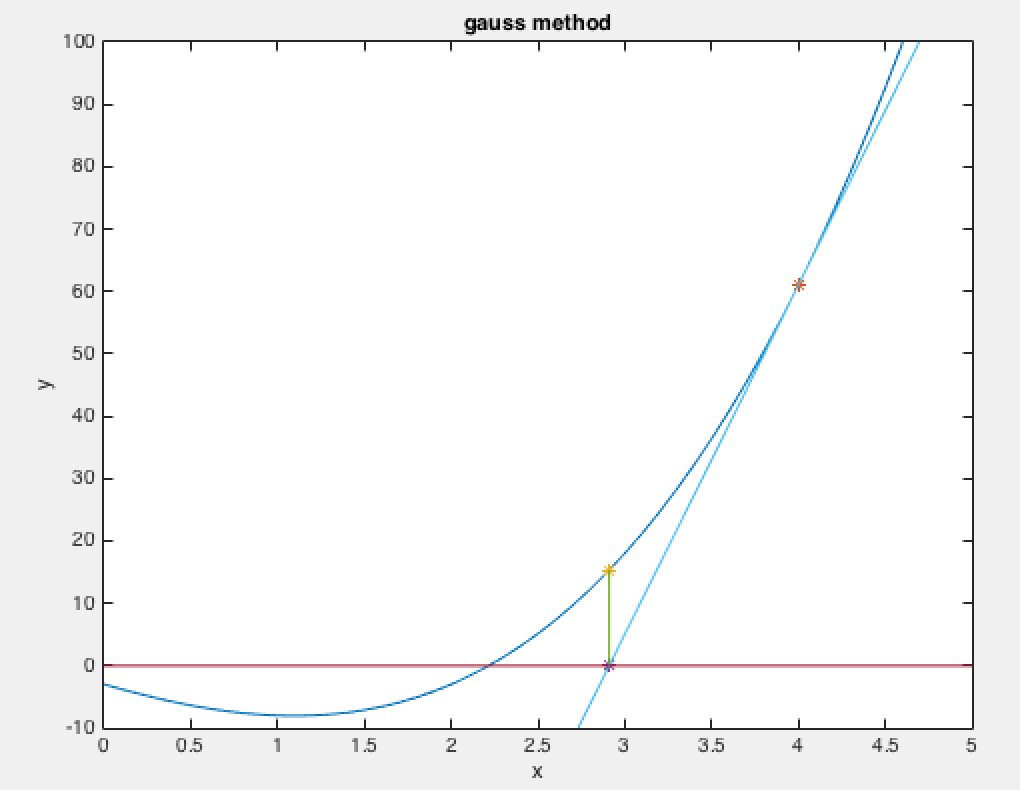
import matplotlib.pyplot as pltdef dampnm(fun,gfun,hess,x0):# 用牛顿法求解无约束问题#x0是初始点，fun，gfun和hess分别是目标函数值，梯度，海森矩阵的函数maxk = 500rho = 0.55sigma = 0.4k = 0epsilon = 1e-5f=open("牛顿.txt","w")W = np.zeros((2, 20000))while k < maxk:W[:, k] = x0gk = gfun(x0)Gk = hess(x0)dk = -1.0*np.linalg.solve(Gk,gk)print(k, np.linalg.norm(dk))f.write(str(k)+'   '+str(np.linalg.norm(gk))+"\n")if np.linalg.norm(dk) < epsilon:breakx0 += dkk += 1W = W[:, 0:k + 1]  # 记录迭代点return x0,fun(x0),k,W# 函数表达式fun
fun = lambda x:100*(x[0]**2-x[1])**2 + (x[0]-1)**2# 梯度向量 gfun
gfun = lambda x:np.array([400*x[0]*(x[0]**2-x[1])+2*(x[0]-1), -200*(x[0]**2-x[1])])# 海森矩阵 hess
hess = lambda x:np.array([[1200*x[0]**2-400*x[1]+2, -400*x[0]],[-400*x[0],200]])if __name__=="__main__":X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)X2 = np.arange(-3.5, 2 + 0.05, 0.05)[x1, x2] = np.meshgrid(X1, X2)f = 100 * (x2 - x1 ** 2) ** 2 + (1 - x1) ** 2  # 给定的函数plt.contour(x1, x2, f, 40)  # 画出函数的20条轮廓线x0 = np.array([-1.2, 1])out=dampnm(fun, gfun, hess, x0)print(out[2],out[0])W = out[3]print(W[:,:])plt.plot(W[0, :], W[1, :], 'g*-')plt.show()

迭代轨迹（但是一直觉得有问题的是为啥第三个点老是会偏辣么多？？）：

迭代的轨迹坐标：

 

 每一步迭代对应的误差：

0	232.8676878
1	4.639426214
2	1370.789849
3	0.473110379
4	25.0274456
5	8.61E-06

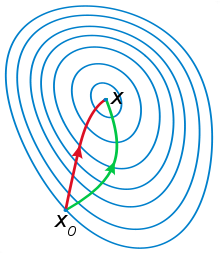
 牛顿法是二阶收敛，最速下降是一阶收敛，所以牛顿法就更快。最速下降法每次只从当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比最速下降法看得更远一点，能更快地走到最底部。牛顿法目光更加长远，所以少走弯路；相对而言，最速下降法只考虑了局部的最优，没有全局思想。

 

注：内容原创，部分文字来源于网络。