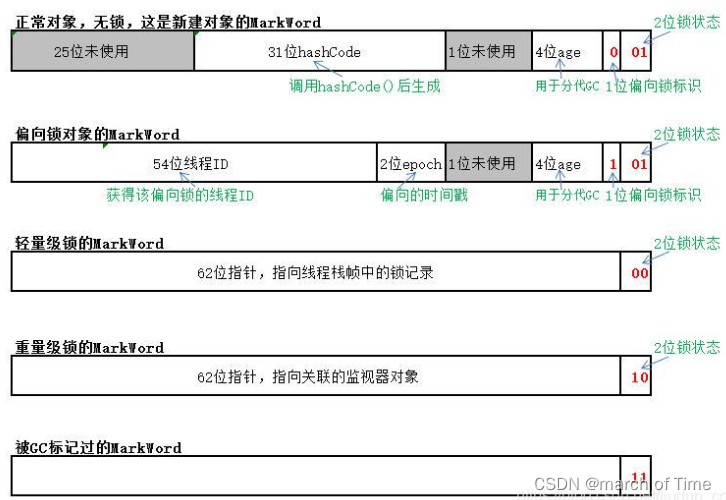
一、牛顿法概述
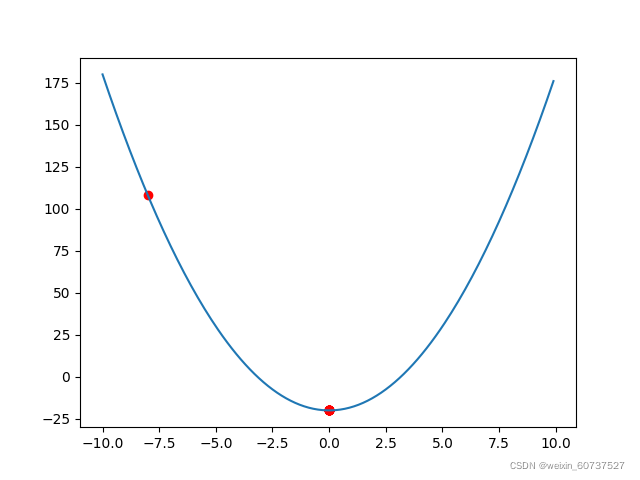
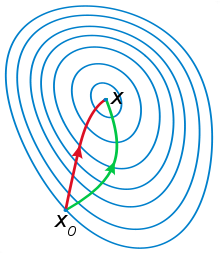
除了前面说的梯度下降法,牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法的基本思想是利用迭代点 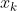 处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。
处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。
二、基本牛顿法
1、基本牛顿法的原理
基本牛顿法是一种是用导数的算法,它每一步的迭代方向都是沿着当前点函数值下降的方向。
我们主要集中讨论在一维的情形,对于一个需要求解的优化函数 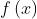 ,求函数的极值的问题可以转化为求导函数
,求函数的极值的问题可以转化为求导函数  。对函数
。对函数 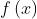 进行泰勒展开到二阶,得到
进行泰勒展开到二阶,得到
对上式求导并令其为0,则为
即得到
这就是牛顿法的更新公式。
2、基本牛顿法的流程
- 给定终止误差值
,初始点
,令
;
- 计算
,若
,则停止,输出
;
- 计算
,并求解线性方程组得解
:
;
- 令
,
,并转2。
三、全局牛顿法
牛顿法最突出的优点是收敛速度快,具有局部二阶收敛性,但是,基本牛顿法初始点需要足够“靠近”极小点,否则,有可能导致算法不收敛。这样就引入了全局牛顿法。
1、全局牛顿法的流程
- 给定终止误差值
,
,
,初始点
,令
;
- 计算
,若
,则停止,输出
;
- 计算
,并求解线性方程组得解
:
;
- 记
是不满足下列不等式的最小非负整数
:
;
- 令
,
,
,并转2。
2、Armijo搜索
全局牛顿法是基于Armijo的搜索,满足Armijo准则:
给定  ,
,  ,令步长因子
,令步长因子  ,其中
,其中 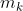 是满足下列不等式的最小非负整数:
是满足下列不等式的最小非负整数:
四、算法实现
实验部分使用Java实现,需要优化的函数  ,最小值为
,最小值为  。
。
1、基本牛顿法Java实现
package org.algorithm.newtonmethod;/*** Newton法* * @author dell* */
public class NewtonMethod {private double originalX;// 初始点private double e;// 误差阈值private double maxCycle;// 最大循环次数/*** 构造方法* * @param originalX初始值* @param e误差阈值* @param maxCycle最大循环次数*/public NewtonMethod(double originalX, double e, double maxCycle) {this.setOriginalX(originalX);this.setE(e);this.setMaxCycle(maxCycle);}// 一系列get和set方法public double getOriginalX() {return originalX;}public void setOriginalX(double originalX) {this.originalX = originalX;}public double getE() {return e;}public void setE(double e) {this.e = e;}public double getMaxCycle() {return maxCycle;}public void setMaxCycle(double maxCycle) {this.maxCycle = maxCycle;}/*** 原始函数* * @param x变量* @return 原始函数的值*/public double getOriginal(double x) {return x * x - 3 * x + 2;}/*** 一次导函数* * @param x变量* @return 一次导函数的值*/public double getOneDerivative(double x) {return 2 * x - 3;}/*** 二次导函数* * @param x变量* @return 二次导函数的值*/public double getTwoDerivative(double x) {return 2;}/*** 利用牛顿法求解* * @return*/public double getNewtonMin() {double x = this.getOriginalX();double y = 0;double k = 1;// 更新公式while (k <= this.getMaxCycle()) {y = this.getOriginal(x);double one = this.getOneDerivative(x);if (Math.abs(one) <= e) {break;}double two = this.getTwoDerivative(x);x = x - one / two;k++;}return y;}}
2、全局牛顿法Java实现
package org.algorithm.newtonmethod;/*** 全局牛顿法* * @author dell* */
public class GlobalNewtonMethod {private double originalX;private double delta;private double sigma;private double e;private double maxCycle;public GlobalNewtonMethod(double originalX, double delta, double sigma,double e, double maxCycle) {this.setOriginalX(originalX);this.setDelta(delta);this.setSigma(sigma);this.setE(e);this.setMaxCycle(maxCycle);}public double getOriginalX() {return originalX;}public void setOriginalX(double originalX) {this.originalX = originalX;}public double getDelta() {return delta;}public void setDelta(double delta) {this.delta = delta;}public double getSigma() {return sigma;}public void setSigma(double sigma) {this.sigma = sigma;}public double getE() {return e;}public void setE(double e) {this.e = e;}public double getMaxCycle() {return maxCycle;}public void setMaxCycle(double maxCycle) {this.maxCycle = maxCycle;}/*** 原始函数* * @param x变量* @return 原始函数的值*/public double getOriginal(double x) {return x * x - 3 * x + 2;}/*** 一次导函数* * @param x变量* @return 一次导函数的值*/public double getOneDerivative(double x) {return 2 * x - 3;}/*** 二次导函数* * @param x变量* @return 二次导函数的值*/public double getTwoDerivative(double x) {return 2;}/*** 利用牛顿法求解* * @return*/public double getGlobalNewtonMin() {double x = this.getOriginalX();double y = 0;double k = 1;// 更新公式while (k <= this.getMaxCycle()) {y = this.getOriginal(x);double one = this.getOneDerivative(x);if (Math.abs(one) <= e) {break;}double two = this.getTwoDerivative(x);double dk = -one / two;// 搜索的方向double m = 0;double mk = 0;while (m < 20) {double left = this.getOriginal(x + Math.pow(this.getDelta(), m)* dk);double right = this.getOriginal(x) + this.getSigma()* Math.pow(this.getDelta(), m)* this.getOneDerivative(x) * dk;if (left <= right) {mk = m;break;}m++;}x = x + Math.pow(this.getDelta(), mk)*dk;k++;}return y;}
}
3、主函数
package org.algorithm.newtonmethod;/*** 测试函数* @author dell**/
public class TestNewton {public static void main(String args[]) {NewtonMethod newton = new NewtonMethod(0, 0.00001, 100);System.out.println("基本牛顿法求解:" + newton.getNewtonMin());GlobalNewtonMethod gNewton = new GlobalNewtonMethod(0, 0.55, 0.4,0.00001, 100);System.out.println("全局牛顿法求解:" + gNewton.getGlobalNewtonMin());}
}