基本思想与迭代公式

通常对已知方程$f(x)=0$进行变形而构造的迭代函数$\phi (x)$不是惟一的。在实际作用中，如果希望迭代函数$\phi (x)$有一种固定格式的构造方法，就可以采用Newton迭代法。

Newton迭代法的基本思想是：设法将一个非线性方程$f(x)=0$转化为某种线性方程求解，其解决问题的基础是Taylor（泰勒）多项式。具体描述如下：

设$f(x)=0$的近似根为$x_k$，则函数$f(x)$在点$x_k$附近可用一阶Taylor多项式$p_1(x)$来近似，即：
$$p_{(}x)=f(x_k)+f^{\prime }(x_k)(x-x_k)\cong f(x)$$
从而得到线性方程：
$$f(x_k)+f^{\prime }(x_k)(x-x_k)=0$$
解之，得该线性方程的根$x$，但它是$f(x)=0$的一个新近似根，记做$x_{k+1}$，即：
$$x_{k+1}=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$$
上式实质上就是一种迭代格式，称为Newton迭代格式。相应地，Newton迭代函数为：
$$\phi (x)=x-\frac{f(x)}{f^{\prime }(x)}\text{\hspace{1em}(1)}$$
于是，按（1）式构造迭代函数解方程$f(x)=0$的方法，就是Newton迭代法。

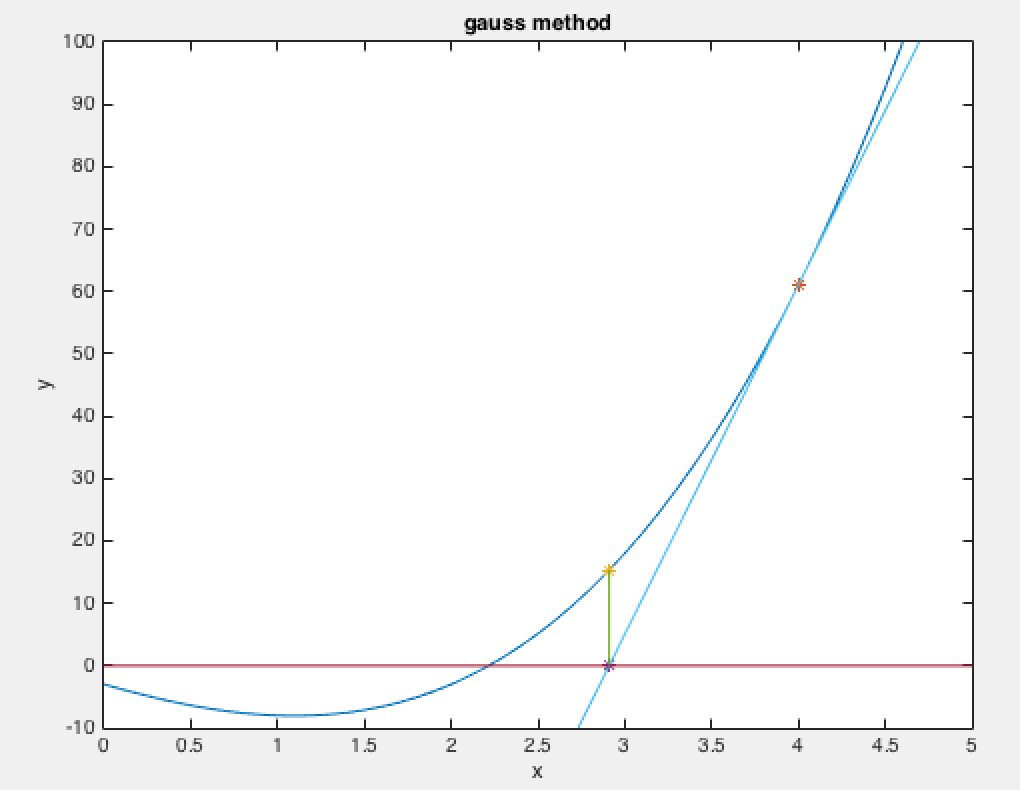
Newton迭代法的几何解释如下图所示。方程$f(x)=0$的根$x^{\ast }$为$y=f(x)$和$y=0$（即x轴）的交点。设$x_k$为$x^{\ast }$的某个初始近似值，过$p_k$点$(x_k,f(x_k))$作$y=f(x)$的切线交x轴于$x_{k+1}$，即为所求得的近似值。继续过$p_{k+1}$点$(x_{k+1},f(x_{k+1}))$，$p_{k+2}$点$(x_{k+2},f(x_{k+2})),\cdots$，作$y=f(x)$的切线，即可逐步逼近精确的根$x^{\ast }$。因此，Newton法也叫切线法，因为它是沿着曲线$y=f()x$上某一点作切线逐步外推逼近的。从$p_k$点作切线与x轴的交点$x_{k+1}$，由于$y=f(x)$不是直线，所以$f(x_{k+1})$就不可能为零。因此必须以$x_{k+1}$作为新的起点，从与之对应的$p_{k+1}$点继续作切线，重复上述步骤，直至$f(x_{k+1})$充分小，逼近零时为止。

例1：用Newton迭代法求方程$x{e}^x-1=0$的根。

解：方程可改写为$x=e^{-x}$，即$f(x)=x-e^{-x}=0$，此方程的Newton迭代格式为：
$$x_{k+1}=x_k-\frac{x_k-e^{-x_k}}{1+e^{-x_k}}=x_k-\frac{x_k-e^{-x_k}}{1+x_k}$$
取迭代初值为$x_0=0.5$，逐次迭代结果为$x_1=0.57102,x_2=0.56716;x_3=0.56714;x_4=0.56714$。由此可见，迭代4次即达到了$|x_4-x_3|\le 0.000005$的要求，收敛速度是很快的。

例2：推导立方根的Newton迭代公式，并求$a=155$的立方根。

解：该问题等价于求$f(x)=x^3-a$的零点，即解方程：
$$f(x)=x^3-a=0$$
运用Newton迭代公式，有：
$$x_{k+1}=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}=x_k-\frac{x_k^3-a}{3x_k^2}=\frac{2}{3}{x}_k-\frac{a}{3x_k^2}$$
令$a=155,x_0=5$，迭代计算结果为：

n	0	1	2	3
x	5	5.4	5.371834	5.371686

仅迭代3步就求得精确解。再使用较差一些的初值$x_0=10$，则迭代计算结果为：

n	0	1	2	3	4	5
x	10	7.183334	5.790176	5.401203	5.371847	5.371686

迭代5步之后得到精确值。

使用Newton法求方程的根，在什么条件下、选取什么样的初始值$x_0$，才能保证迭代过程总是收敛于方程的根的根$x^{\ast }$呢？这是运用Newton法求方程根的重要问题。