牛顿法（Newton Method）

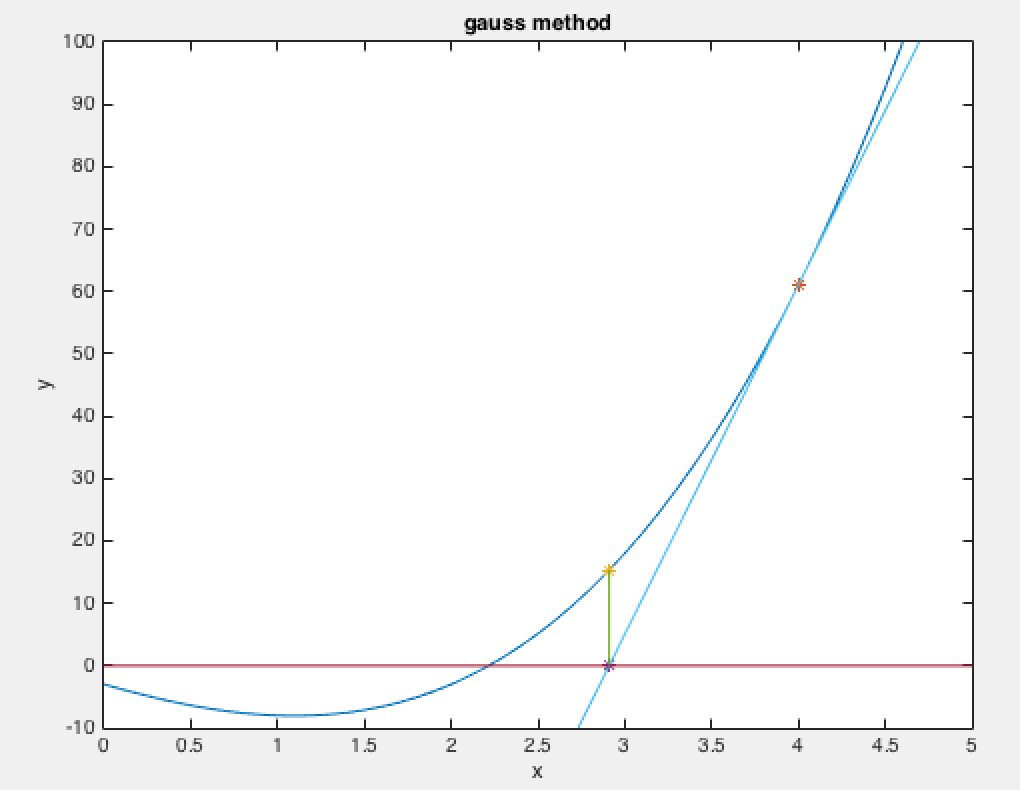
牛顿法与梯度下降法，最速下降法等优化算法类似，是基于梯度的方法。给定一个二次可微的凸目标函数$f(x)$，将其在点$x_k$处泰勒展开到二阶：
$$f(x)=f(x_k)+▽f(x_k)(x-x_k)+\frac{1}{2}{▽}^{2}f(x_k)(x-x_k{)}^2，\text{\hspace{1em}(1)}$$
两边同时对$x$进行求导得到$▽f(x)=▽f(x_k)+{▽}^{2}f(x_k)(x-x_k)$。实际上求$f(x)$的最小值的过程，可以转化成求$△f(x)=0$的过程。因此令$▽f(x)=0$，我们就得到了基本牛顿法的更新规则：
$$x=x_k-{▽}^{2}f(x_k{)}^{-1}▽f(x_k).\text{\hspace{1em}(2)}$$
其中，$▽x_k=-{▽}^{2}f(x_k{)}^{-1}▽f(x_k)$称为牛顿步。由于${▽}^{2}f(x_k)$的正定性，我们可以得到：
$$▽f(x_k)▽x_k=-▽f(x_k){▽}^{2}f(x_k{)}^{-1}▽f(x_k)<0\text{\hspace{1em}(3)}$$
因此，$▽x_k$牛顿步是函数值下降的方向。但是经过实践发现，基本牛顿法的步长有时候可能会过大，它的初始点需要足够的“靠近“极小值点，否则可能会导致算法不收敛(我就遇到这种情况)。所以有人提出了全局牛顿法，基于Armijio搜索寻找一个合适的步长。全局牛顿法的算法如下（参考Stephen Boyd的convex optimzation一书）：

对数障碍函数方法

我们考虑一个一般形式的优化问题：
$$\begin{gathered} \text{minimize}{f}_0(x) \\ s.t.f_i(x)\le 0,i=1,2,...,m \\ Ax=b\text{\hspace{1em}(4)} \end{gathered}$$
障碍法的思想是通过向目标函数中添加一个障碍函数（或者惩罚函数）来去掉优化问题中的不等式约束。把原优化问题的形式转化成如下的形式：
$$\begin{gathered} \text{minimize}{f}_0(x)+\sum _{i=1}^m{I}_{\_}(f_i(x)) \\ s.t.Ax=b\text{\hspace{1em}(5)} \end{gathered}$$
其中$I_{\_}(u)$是这样一个函数：
$$I_{\_}(u)\{\begin{array}{ll}0& u\le 0,\\ \infty & u>0.\end{array}\text{\hspace{1em}(6)}$$
其实就是在不等式约束的边界竖起一堵”墙“。当满足约束时，$I_{\_}(u)$值为0；当破坏约束时，$I_{\_}(u)$值为无穷，对函数值进行惩罚。对数障碍方法利用如下的障碍函数：
$$I_{\_}(u)=-\frac{1}{t}log(-u),u<0\text{\hspace{1em}(7)}$$
将其带入到上面的优化问题(5)可得到如下的优化问题：
$$\begin{gathered} \text{minimize}t{f}_0(x)+\sum _{i=1}^m-log(-f_i(x)) \\ s.t.Ax=b\text{\hspace{1em}(8)} \end{gathered}$$
其中，目标函数函数是凸的，因为$-\frac{1}{t}log(-u)$关于$u$是凸的，两个凸函数相加仍然是凸的。因此，我们可以用牛顿法进行求解。我们定义$x^{\ast }(t)$为问题(8)最优解，$p^{\ast }$为原问题(4)的最小值，通过central path（具体可看convex optimization 第11章）的分析，可以得到：
$$f(x^{\ast }(t))-p^{\ast }\le \frac{m}{t},\text{\hspace{1em}(9)}$$
从(9)中可看出当$t$逐渐增大，$x^{\ast }(t)$最终可以收敛到最小值值点。$f(x^{\ast }(t))-p^{\ast }$称为对偶gap。对数障碍法的算法如下：
实际上，障碍法的外层是对参数$t$的更新，内层利用牛顿迭代法求解最优值。当$u$设置的比较大的时候，外层更新的次数比较少，但是内层牛顿法迭代的次数增加。反之则相反，因此需要寻找合适的$u$，通常设置 u ∈ { 10 , 20 } u \in \{10, 20\} u∈{10,20}.

一个简单的例子

考虑一个简单的优化问题：n
$$\begin{gathered} \text{minimize}{c}^{T}x \\ s.t.x⪰0.\text{\hspace{1em}(10)} \end{gathered}$$

python代码

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import math as math# 目标函数
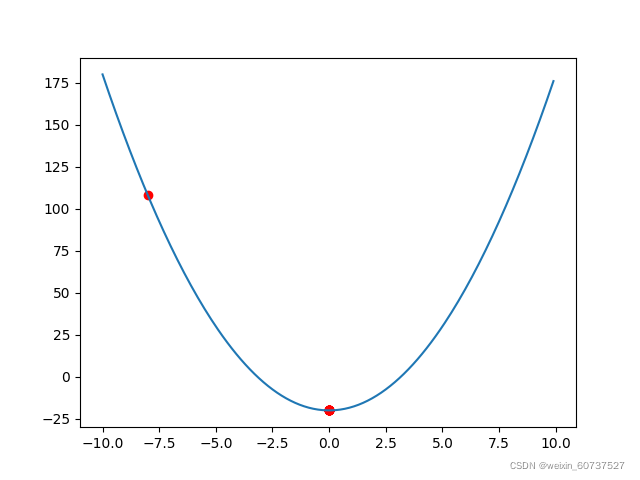
def fun(x, t):result = 0for i in range(x.size):if (x[i] <= 0):return float("inf")result += t * x[i] - np.log2(x[i])return result# 基于对数障碍法的内点法
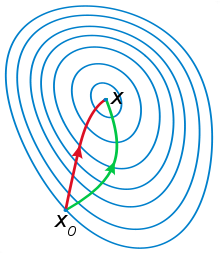
def logBarriar():# 初始值m = 2t = 4x = np.array([1.3, 1])  # 初始点epsilon = 0.001  # 障碍函数法阈值mu = 10x = newtonMethod(x, t)while m / t > epsilon:# 更新tt = mu * t# 全局牛顿迭代求解t*f(x)+Φ*(x)的最值x = newtonMethod(x, t)# 全局牛顿迭代法
def newtonMethod(x_0, t):x = x_0epsilon = 0.00001  # 牛顿法阈值g = np.array(np.array([t, t]) - 1 / (x * np.log(2)))H = np.array([[1 / (math.pow(x[0], 2) * np.log(2)), 0], [0, 1 / (math.pow(x[1], 2) * np.log(2))]])delta_x = - np.matmul(g, np.linalg.inv(H.T))lambda_2 = np.matmul(np.matmul(g, np.linalg.inv(H.T)), g.T)trace = [[], []]  # 迭代轨迹while lambda_2 / 2 > epsilon:# 添加到迭代轨迹trace[0].append(x[0])trace[1].append(x[1])# 回溯线性搜索确定步长alpha = 0.1beta = 0.5k = 1  # 步长while fun(x + k * delta_x, t) > fun(x, t) + alpha * k * lambda_2:k = beta * k# 更新xx = x + k * delta_x# 目标函数的一阶导g = np.array(np.array([t, t]) - 1 / (x * np.log(2)))# 目标函数的Hessian矩阵H = np.array([[1 / (math.pow(x[0], 2) * np.log(2)), 0], [0, 1 / (math.pow(x[0], 2) * np.log(2))]])# 下降方向delta_x = - np.matmul(g, np.linalg.inv(H.T))# 牛顿增量lambda_2 = np.matmul(np.matmul(g, np.linalg.inv(H.T)), g.T)# 定义坐标轴ax1 = plt.axes(projection='3d')# 绘制三维函数图像x_1 = np.arange(0.1, 1.5, 0.1)x_2 = np.arange(0.1, 1.5, 0.1)xx_1, xx_2 = np.meshgrid(x_1, x_2)z = t * (xx_1 + xx_2) - (np.log2(xx_1) + np.log2(xx_2))ax1.plot_surface(xx_1, xx_2, z, cmap='rainbow')plt.show()# 绘制等高线plt.contour(xx_1, xx_2, z, 5, color='black')plt.plot(trace[0], trace[1], marker='X', color='b')plt.show()return xif __name__ == '__main__':logBarriar()

初始值为$c=\left(\begin{array}{c}1\\ 1\end{array}\right)$, $t=4$, $x=(1.3,1)$。下图是第一次迭代时，(8)的目标函数的图像和等高线以及迭代路径：